Featured Fundamentals Resources
[no_toc]
Understanding Specific Gravity: Key Concept in Fluid Mechanics
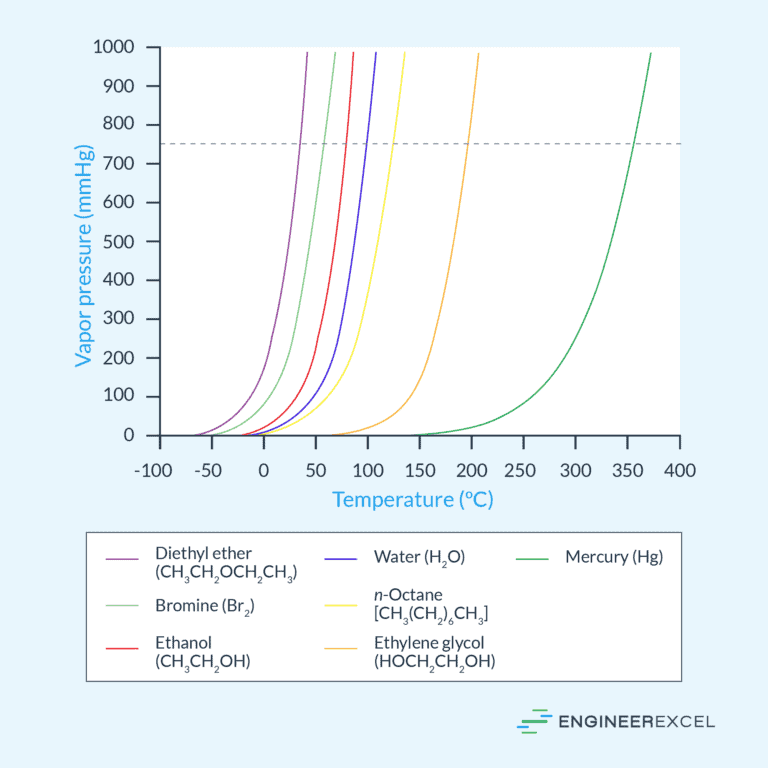
Vapor Pressure: A Comprehensive Overview
Gas Expansion: Understanding the Basics and Applications in Engineering
Shear Strain Rate: Understanding Its Significance in Fluid Mechanics
Understanding Newtonian Fluids: Characteristics and Examples
Ideal Gas Law: Essential Principles and Applications in Thermodynamics
Gas Compression: Fundamentals and Practical Applications in Engineering
Incompressible Fluid: Dynamics and Fundamental Concepts
Speed of Sound: A Guide to Understanding and Measuring Acoustic Velocity
Understanding the No Slip Boundary Condition in Fluid Dynamics
Non-Newtonian Fluids: Classifications and Applications in Engineering
Surface Tension: Understanding Fluid Stability and Interaction
Absolute Pressure in Fluid Systems: Navigating the Fundamentals
Isothermal Process: Fundamentals and Applications in Engineering Systems
Understanding Isentropic Process in Fluid Mechanics and Thermodynamics
Dynamic vs Kinematic Viscosity: Understanding Key Differences
Fluid mechanics is the study of the behavior of fluids, including liquids and gases, and the principles governing their motion. It involves the analysis of fluid flow, pressure, velocity, and other properties to understand and predict the behavior of fluids in various situations.

In this article, we will discuss essential concepts in fluid mechanics, including the properties of fluids and the different fluid classifications based on their characteristics and behavior.
Introduction to Fluid Mechanics

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
A fluid is a substance that continues to deform under an applied shear stress. Fluids can be classified into two categories: liquids and gases. Liquids have a constant volume and typically take the shape of the container, while gases have variable volume and can expand to fill any volume available.
Fluid mechanics is the branch of engineering that deals with the behavior, control, and properties of fluids in motion or at rest. It encompasses two main categories: fluid statics, which focuses on the behavior of fluids at rest, and fluid dynamics, which is concerned with the motion of fluids.
Fluid mechanics is essential in understanding and solving problems in various fields. For example, in aerospace engineering, the study of fluid mechanics plays an important role in designing aircraft, as it involves understanding the aerodynamic forces acting on the wings and fuselage, leading to efficient designs for lift, drag, and maneuverability.
In mechanical engineering, fluid mechanics is essential in designing and analyzing systems like pumps, turbines, and hydraulic systems. For instance, understanding fluid flow in pipes is important in the selection and sizing of pumps in various industries.
In civil engineering, fluid mechanics also plays a significant role in the design and analysis of structures such as dams, bridges, and water distribution systems. For example, engineers must understand the behavior of fluids in determining the forces acting on submerged structures and design systems to manage floods and control erosion.
Lastly, in environmental engineering, fluid mechanics is vital in analyzing pollutant transport and dispersion in water and air. It also contributes to the design of wastewater treatment plants, air pollution control systems, and natural resource management.
Properties of Fluids
Pressure
Fluid pressure is the force per unit area exerted by a fluid, such as a liquid or gas, on the walls of its container. This can be measured two ways: absolute pressure and gauge pressure.
Absolute pressure is the total pressure exerted by a fluid, including atmospheric pressure, measured relative to a perfect vacuum. Gauge pressure, on the other hand, is the pressure measured relative to atmospheric pressure, excluding the atmospheric pressure itself.
Temperature
Temperature is a measure of the thermal energy possessed by a fluid. It refers to the degree of hotness or coldness of a fluid, typically expressed in degrees Celsius (°C) or Fahrenheit (°F). The temperature of a fluid influences several of its other physical properties, including viscosity and density.
Density and Specific Gravity
Density is a measure of mass per unit volume. It quantifies how much matter is packed into a given space.
Specific gravity, on the other hand, is a dimensionless ratio comparing the density of a substance to the density of a reference substance, usually water. It provides a relative measure of how heavy a substance is compared to an equal volume of water.
Both density and specific gravity are used to characterize and differentiate various liquids and solids based on their mass and buoyancy properties.
Internal Energy
The internal energy of a fluid represents the sum of its microscopic kinetic and potential energy at the molecular level. It includes both translational and vibrational motion of molecules within the fluid. Changes in internal energy can occur through processes such as heating or compression, influencing the fluid’s temperature and pressure.
Enthalpy
Enthalpy is a thermodynamic property of a fluid that combines its internal energy and the product of pressure and volume. It is expressed mathematically as:
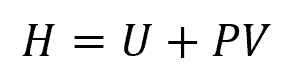
Where:
- H = enthalpy [J]
- U = internal energy [J]
- P = fluid pressure [Pa]
- V = volume of the fluid [m3]
Enthalpy is particularly useful in analyzing heat transfer processes and is commonly employed in thermodynamics to describe energy changes in fluids under varying conditions.
Entropy
Entropy is a measure of the disorder or randomness within a fluid’s molecular arrangement. In thermodynamics, it is denoted by the symbol “S” and is associated with the amount of thermal energy in a system that cannot be converted into useful work. The concept of entropy helps describe the tendency of a fluid to evolve towards a state of greater disorder and is a key parameter in understanding the spontaneity of thermodynamic processes.
Specific Heats
Specific heat refers to the amount of heat energy required to raise the temperature of a unit mass of a fluid by one degree Celsius or Kelvin. There are two specific heat values associated with fluids: the specific heat at constant volume (Cv) and the specific heat at constant pressure (Cp). These parameters are important in understanding how fluids respond to changes in temperature and pressure, playing a fundamental role in thermodynamics and heat transfer analysis.
Dynamic Viscosity and Kinematic Viscosity
Viscosity is a measure of a fluid’s internal resistance to flow or deformation. It is often described as the thickness or stickiness of a fluid. High viscosity fluids, such as molasses or honey, flow more slowly, while low viscosity fluids, like water, flow more easily.
The two primary types of viscosity are dynamic viscosity, which measures the internal friction as a fluid shears, and kinematic viscosity, which considers the dynamic viscosity in relation to the fluid’s density.
Thermal Conductivity
Thermal conductivity is a material property that describes the ability of a substance to conduct heat. In the context of fluids, such as liquids and gases, thermal conductivity indicates how efficiently the fluid can transfer heat through conduction. Different fluids exhibit varying thermal conductivities, and this property is essential in understanding and analyzing heat transfer processes.
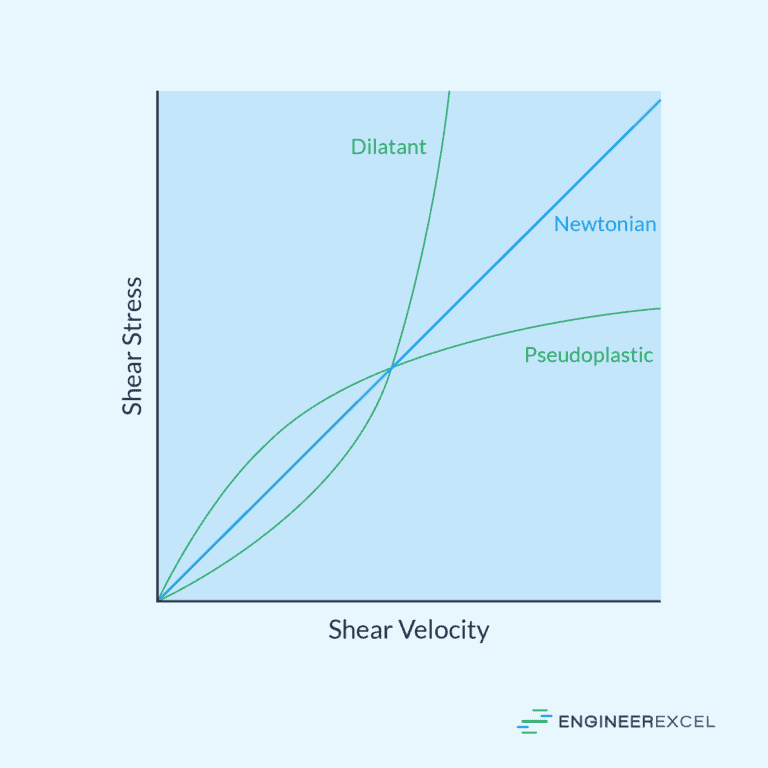
Newtonian vs Non-Newtonian Fluids
In fluid mechanics, fluids are classified into two main categories: Newtonian fluids and non-Newtonian fluids. These classifications are based on the relationship between the fluids’ shear stress and shear rate.
Newtonian Fluids
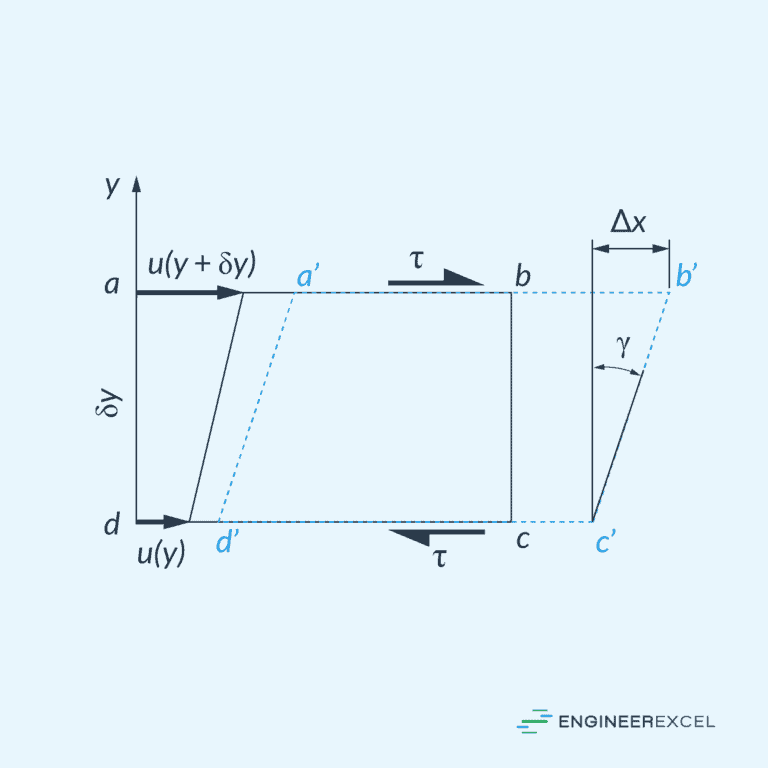
Newtonian fluids are characterized by a linear relationship between the shear stress (τ) and the shear rate (γ). The constant of proportionality between these two quantities is known as the fluid’s viscosity (μ), which is a measure of the fluid’s resistance to deformation.
Some common examples of Newtonian fluids include water, air, and mineral oil. The viscosity of Newtonian fluids remains constant, irrespective of the shear rate, under constant temperature and pressure conditions.
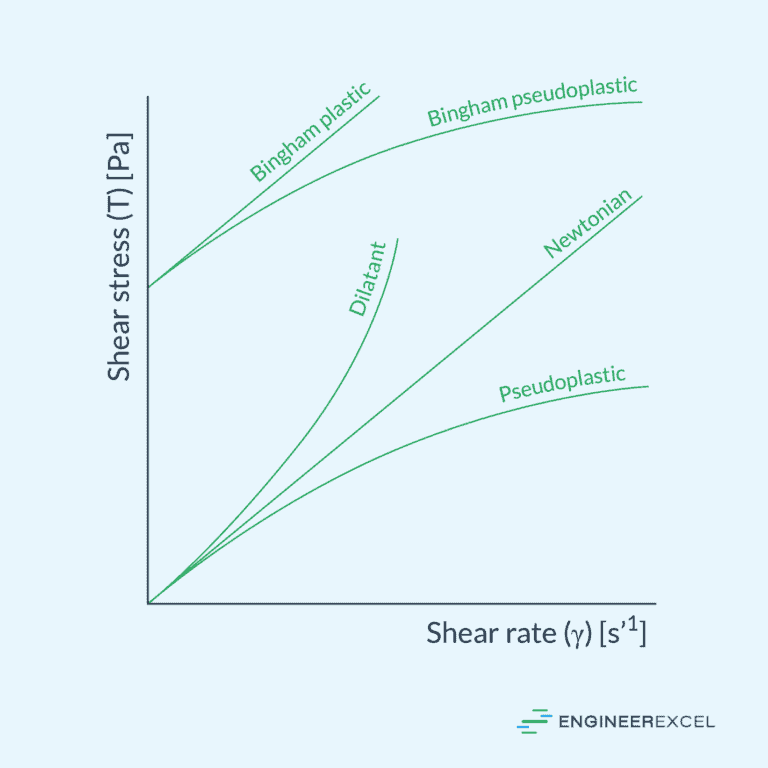
Non-Newtonian Fluids
Non-Newtonian fluids, on the other hand, exhibit a nonlinear relationship between the shear stress and the shear rate. Their apparent viscosity (μ’) may change as a function of the applied shear rate. Non-Newtonian fluids can be further divided into multiple categories based on their behavior under different shear rates:
- Shear-thinning fluids: Also known as pseudoplastic fluids, these fluids exhibit a decrease in viscosity as the shear rate increases. Examples include ketchup and paint.
- Shear-thickening fluids: Also called dilatant fluids, the viscosity of these fluids increases with increasing shear rate. Cornstarch mixed with water is a common example of a shear-thickening fluid.
- Bingham-plastic fluids: These fluids exhibit a finite yield stress, which must be surpassed before flow can occur. Common examples include toothpaste and mayonnaise.
- Thixotropic fluids: The viscosity of these fluids decreases over time when subjected to a constant shear stress. They have a time-dependent response. Examples include certain gels and paints.
- Rheopectic fluids: Opposite to thixotropic fluids, the viscosity of rheopectic fluids increases over time under constant shear stress. Some lubricants and certain clays exhibit this behavior.
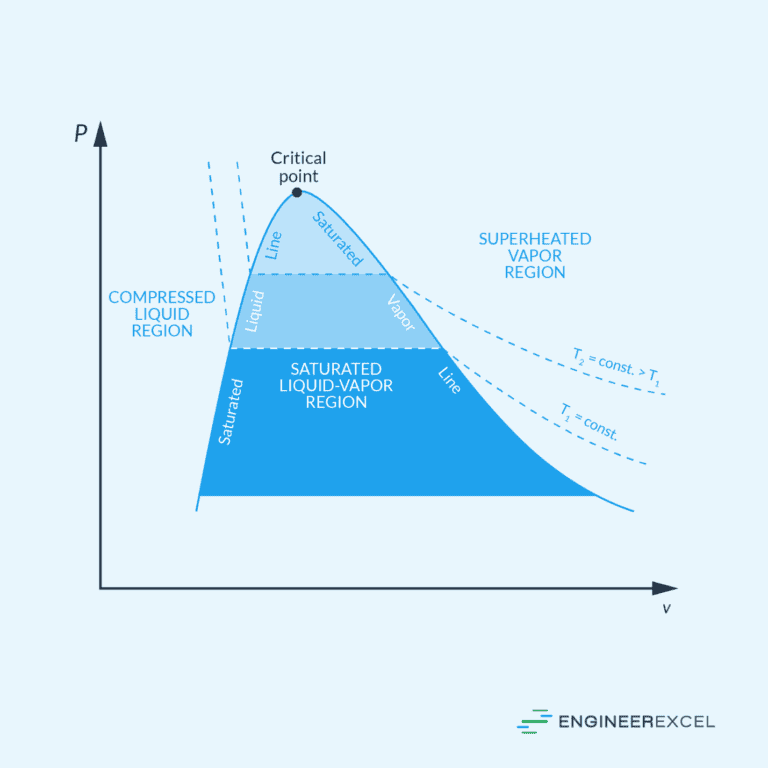
Incompressible vs Compressible Fluids
Fluids can also be categorized between incompressible and compressible fluids. These two types of fluids exhibit distinct characteristics and behaviors, which make a significant impact on the governing equations and the corresponding analysis techniques used in solving fluid mechanics problems.

Incompressible fluids are those whose density remains constant as they flow; that is, their volume doesn’t change under pressure variations. This assumption simplifies the analysis of fluid flow, especially in cases where fluid velocities are relatively low, and pressure changes are not significant. Examples of incompressible fluids include water and other liquids.
On the other hand, compressible fluids exhibit changes in density in response to pressure and temperature variations. The analysis of compressible fluid flow is important when dealing with high-speed flows or significant pressure changes, such as those encountered in aerodynamics and propulsion systems. Gases, like air, are commonly treated as compressible fluids.
Compressible Flow
Compressible flow deals with fluid behavior when the density changes significantly due to variations in pressure and temperature. This is particularly relevant in high-speed applications, such as aerospace and gas dynamics.
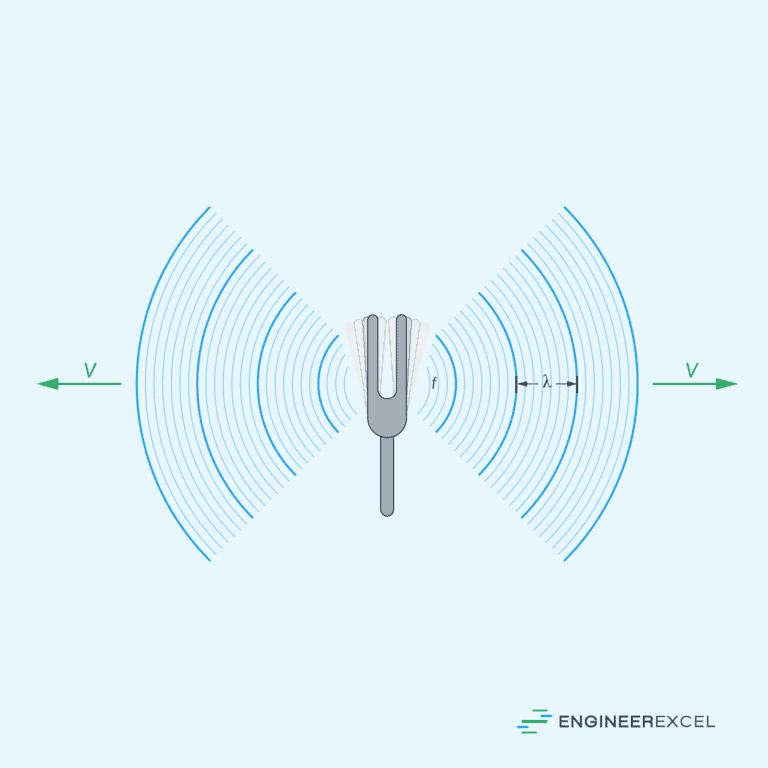
Speed of Sound
The speed of sound refers to the speed at which pressure disturbances propagate through a fluid. For an ideal gas, the speed of sound can be determined using the relation:

Where:
- v = speed of sound [m/s]
- γ = specific heat ratio or adiabatic index [unitless]
- R = gas constant [8.314 J/mol-K]
- T = temperature [K]
- M = molecular mass [kg/mol]
Ideal Gas Law
The Ideal Gas Law is another principle that is commonly applied in compressible flow. For ideal gases, it states that the product of pressure and volume is directly proportional to the product of the amount of substance and the absolute temperature, as shown in the following equation:
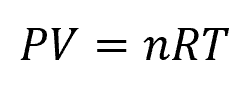
Where:
- P = pressure [Pa]
- V = volume [m3]
- n = number of moles [mol]
- R = gas constant [8.314 J/mol-K]
- T = temperature [K]
The ideal gas law is applicable under conditions where gas particles are not subject to interparticle interactions. This typically happens at higher temperatures and lower pressures, where the potential energy resulting from intermolecular forces between gas particles becomes less significant compared to the particles’ kinetic energy, and the size of the molecules becomes less significant compared to the empty space between them.
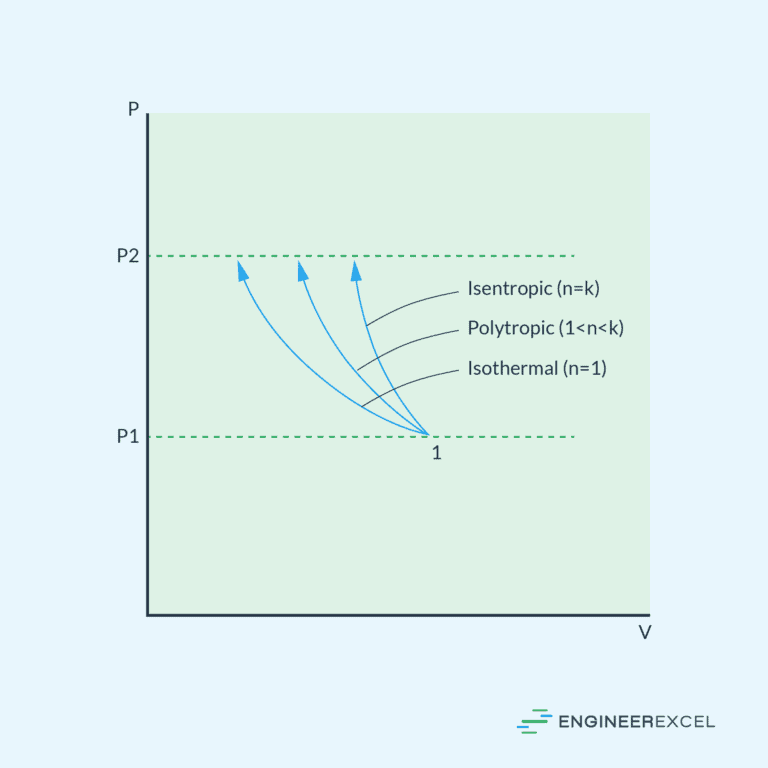
Thermodynamic Processes
In compressible flow, various thermodynamic processes govern the behavior of fluids. These thermodynamic processes can be classified based on the following key categories:
Isothermal Process
In an isothermal process, the temperature of the fluid remains constant throughout the compression or expansion. This implies that the internal energy of the fluid does not change during the process.
Adiabatic Process
An adiabatic process involves no heat exchange with the surroundings. In this process, the system is insulated, preventing the transfer of heat. As a result, the change in internal energy is solely due to work done on or by the system.
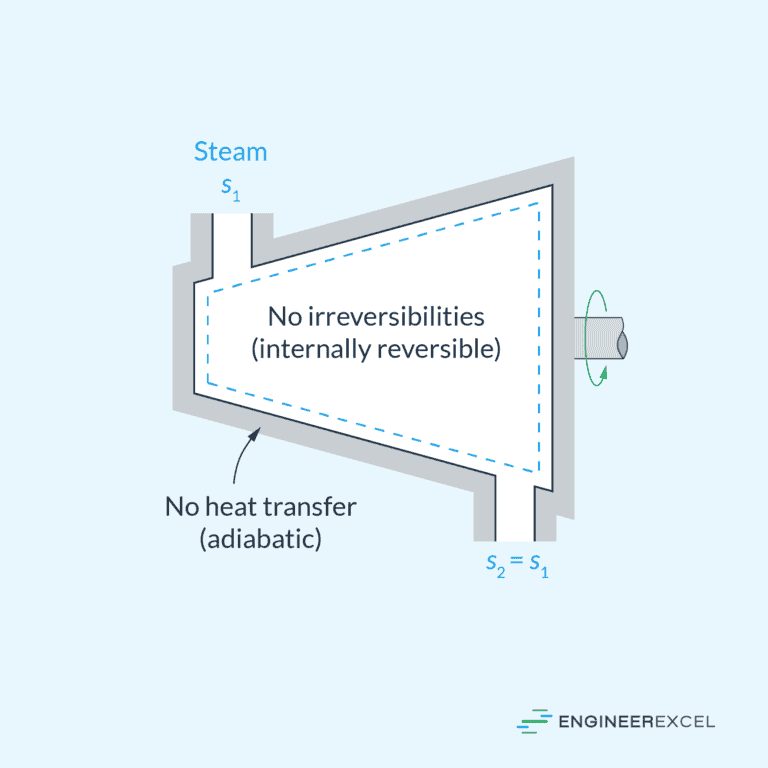
Isentropic Process
An isentropic process is an idealized adiabatic process that is also reversible. In this process, entropy remains constant. It is often referred to as adiabatic, but it specifically pertains to a reversible adiabatic process.
Isobaric Process
In an isobaric process, the pressure of the fluid remains constant. While the volume and temperature may change, the pressure remains unchanged during compression or expansion.
Isochoric Process
In an isochoric process, the volume of a system remains constant. The system may undergo changes in internal energy and temperature, but without any work being done on or by the system through volume changes.