The no-slip boundary condition is a condition in fluid dynamics that asserts that at a solid surface, the fluid velocity is zero relative to the surface. This implies that the fluid adheres to and moves with the solid surface, resulting in a velocity of zero at the boundary.

In this article, we will define the no-slip boundary condition and discuss its significance in fluid systems, as well as its limitations and assumptions.
No-Slip Boundary Condition Explained
Formulating a problem in fluid mechanics requires not only specifying the governing equations but also defining the appropriate boundary conditions. These conditions determine the interactions between the fluid and its surroundings and are important in obtaining meaningful and accurate solutions to fluid mechanics problems.
When a fluid comes into contact with a solid surface, two different boundary conditions are typically applied. The first condition states that there is no flow across the surface, meaning there is zero normal velocity. The second condition states that there is no flow along the boundary, resulting in zero tangential velocity.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
This latter condition is often referred to as the no-slip boundary condition, which is based on the observation that fluid flow sticks to the surface of a solid body. This implies that, at the surface of a solid boundary, the fluid velocity is equal to the solid’s velocity. In other words, the fluid is considered to be stationary with respect to the solid body, resulting in no relative velocity across the boundary.
This is illustrated in the diagram below.
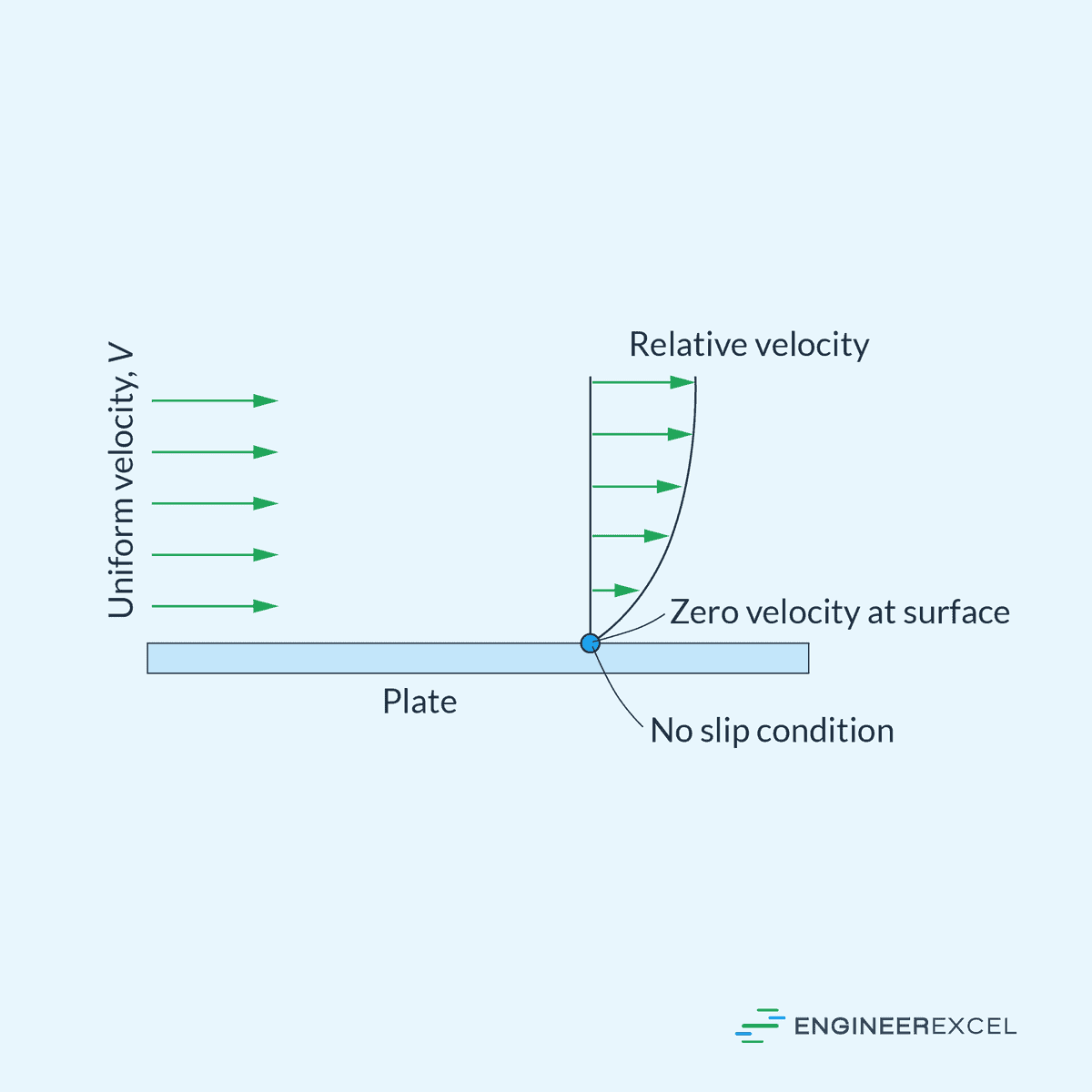
The no-slip boundary condition is a consequence of the fluid’s viscosity, which prevents the fluid from immediately “slipping” over the surface. This condition is significant in solving problems related to fluid mechanics and is widely applied in many engineering fields, such as aerodynamics and heat transfer.
It can be mathematically expressed as:
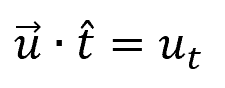
Where:
- = fluid velocity vector [m/s]
- = unit vector tangential to the surface [unitless]
- = velocity of the tangential surface [m/s]
It can be understood in terms of the molecular kinetic theory. At the interface between a solid surface and a fluid, there is an exchange of momentum due to interactions between fluid molecules and the solid surface. Fluid molecules that are in direct contact with the solid surface experience strong molecular forces with the surface molecules, which causes them to essentially stick to it, resulting in zero velocity at the surface.
Boundary Layers
From a fluid dynamics perspective, the no-slip boundary condition arises from the viscous nature of fluids. Fluids exhibit viscous behavior due to internal friction caused by molecular interactions, which leads to velocity gradients within the fluid. Such gradients result in shear stresses, which reflect the internal resistance to deformation caused by the fluid’s motion.
It is essential to consider the no-slip boundary condition in fluid mechanics when analyzing boundary layers. Boundary layers are thin regions in the vicinity of the solid surface where viscous effects are significant. Naturally, the no-slip condition is responsible for creating the boundary layer itself since it forces the fluid to slow down near the surface, resulting in a region of high velocity gradient, as shown in the diagram below.
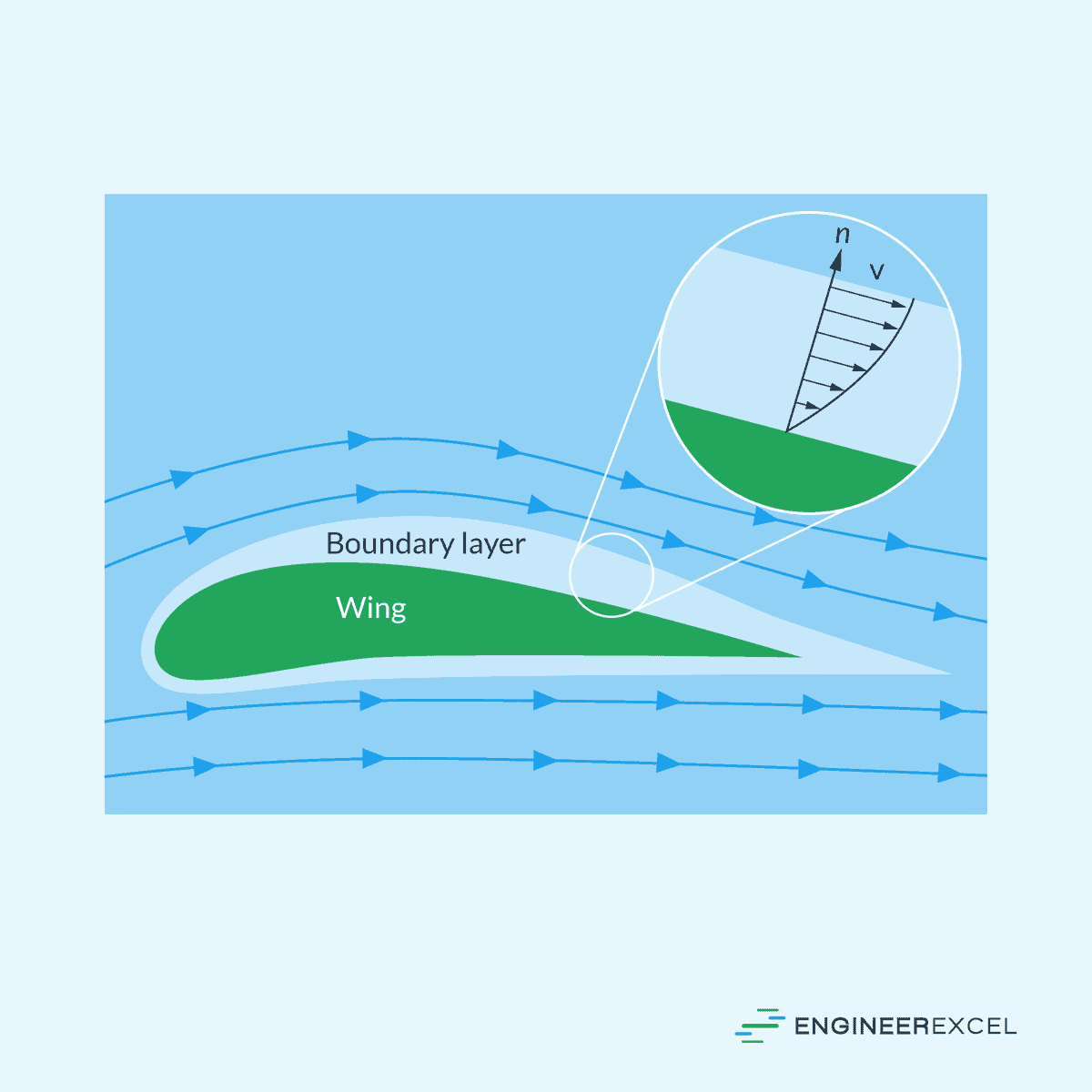
Application of No-Slip in Fluid Mechanics
The interaction of the fluid with solid boundaries ultimately affects the velocity field, pressure distribution, and flow patterns. Hence, the no-slip boundary condition plays an important role in solving the Navier-Stokes equations for fluid dynamics problems.
In the context of computational fluid dynamics (CFD), the no-slip condition is applied by imposing the velocity components of the fluid at the boundary nodes equal to the boundary velocity, typically considered as zero for stationary walls. Incorporating this condition is essential for accurate CFD simulations of industrial applications, such as aerodynamics, heat transfer, and turbulent flow predictions.
CFD simulations involve solving the Navier-Stokes equations using numerical methods, like the finite element method or finite difference method. Implementing the no-slip condition appropriately is essential to ensure convergence and stability of the numerical solution.
Limitations and Assumptions
While the no-slip boundary condition is widely used in fluid mechanics, there are some limitations and assumptions that need to be taken into consideration.
The no-slip boundary condition assumes that the fluid is in contact with a fixed, solid surface. However, not all cases have such surfaces. For example, in porous media or open channel flows, the condition might not fully apply.

In certain microscale flows with very low densities, such as those encountered in microelectromechanical systems (MEMS), there can be observable slip velocity at the surface, leading to a deviation from the classical no-slip condition. In these cases, alternative boundary conditions such as the Navier slip boundary condition may be more appropriate.
The no-slip boundary condition also assumes that fluid particles stick to a solid surface. This might not hold true for certain fluids (e.g., superfluids) that can maintain flow without sticking to the surfaces, which leads to a slip along the boundary.
Lastly, the no-slip boundary condition is most applicable in cases involving Newtonian fluids governed by Newton’s law of viscosity. In the case of non-Newtonian fluids, such as some polymers or foams, the behavior may deviate from this condition, and alternative approaches would need to be considered.
