The Reynolds Number is a dimensionless quantity used in fluid mechanics to predict the flow patterns in different fluid flow situations. It is defined as the ratio of inertial forces to viscous forces and is important in determining whether a flow is laminar or turbulent.

In this article, we will cover the Reynolds number formula, the factors that influence it, and the generalized Reynolds number for non-Newtonian fluids, and how the Reynolds number is used to categorize fluid flow into different regimes.
Reynolds Number Formula
Named after Osborne Reynolds, who introduced it in the late 19th century, the Reynolds number (Re) is a dimensionless quantity defined as the ratio of the inertial forces to the viscous forces of a moving fluid.
Inertial forces are associated with the motion of the fluid. According to Newton’s first law, an object in motion tends to stay in motion unless acted upon by an external force. In the context of fluid flow, this means that inertial forces keep the fluid moving.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Viscous forces, on the other hand, refer to the fluid’s resistance to deformation or flow. The higher the viscosity, the more resistant the fluid is to flow.
By gauging the relative magnitudes between these two forces, the Reynolds number is able to predict the flow patterns in different fluid flow situations. It is expressed mathematically as:
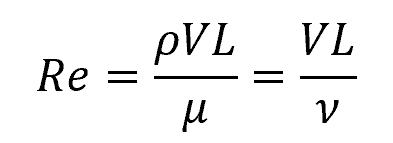
Where:
- Re = Reynolds number [unitless]
- ρ = density of the fluid [kg/m3]
- V = velocity of the fluid relative to the object [m/s]
- L = characteristic length of the flow [m]
- μ = dynamic viscosity of the fluid [Pa-s]
- ν = kinematic viscosity of the fluid [m2/s]
A higher Reynolds number indicates that inertial forces dominate, and the flow is more likely to be chaotic and less affected by viscosity. A lower Reynolds number suggests that viscous forces are more significant, leading to slower and more organized flow.
Factors Affecting Reynolds Number
As shown in the formula above, several factors affect the Reynolds number in a given fluid flow situation:
- Characteristic Length: The characteristic length is a measure of the size of the object or the flow channel. For example, in a pipe, it can be the diameter, and for an airfoil, it can be the chord length. Longer characteristic lengths result in higher Reynolds numbers.
- Fluid Density: The density of a fluid is a measure of its mass per unit volume. The higher the density, the higher the inertial forces within the fluid and, in turn, higher Reynolds number.
- Viscosity: Viscosity is a measure of a fluid’s internal resistance to flow, reflecting the degree of friction between its layers. Fluids with high viscosity, like honey, resist deformation and flow more slowly, while low-viscosity fluids, like water, flow more easily. Hence, the higher the viscosity, the lower the Reynolds number.
- Fluid Velocity: Fluid velocity should be measured relative to the object or conduit. In general, higher velocities lead to higher Reynolds numbers.
Generalized Reynolds Number Formula for Non-Newtonian Fluids
The formula discussed above applies specifically to Newtonian fluids, which demonstrate a linear connection between shear stress and shear rate in accordance with Newton’s law of viscosity. For these fluids, viscosity remains constant regardless of the applied force or rate of deformation.

On the other hand, there are fluids known as non-Newtonian fluids that do not conform to this principle. In these fluids, the relationship between shear stress and strain rate is not linear. Hence, accurately calculating Reynolds number can be challenging due to the variations in viscosity.
A generalized Reynolds number has been proposed, accounting for the behavior of various non-Newtonian fluids, such as Herschel-Bulkley, Ostwald de-Waele, and Bingham-type fluids.
Generalized Reynolds number for non-Newtonian fluids can be derived by considering the appropriate rheological model for a specific fluid. For instance, a simple approach includes the use of an apparent viscosity, determined by the fluid’s shear rate, as shown in the following equation:
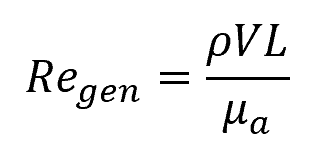
Where:
- Regen = generalized Reynolds number [unitless]
- μa = apparent viscosity of the fluid [Pa-s]
However, this method has limitations when dealing with circular pipe flow, as the shear rate varies at different radial distances from the pipe center.
A more comprehensive approach is using the Herschel-Bulkley-Extended (HBE) generalized Reynolds number. The mathematical formulation for HBE varies based on the specific characteristics of the fluid and the flow conditions. However, in general, this involves modifying the conventional Reynolds number equation to include parameters relevant to the Herschel-Bulkley model and the flow behavior of non-Newtonian fluids.
These parameters encompass the rheological properties of the fluid, including the consistency index, which measures the fluid’s resistance to flow; the flow behavior index, which represents the relationship between shear stress and shear rate; and the yield stress, which is the minimum stress needed to initiate flow.
Reynolds Number and Fluid Flow Regimes
The value of the Reynolds number is used to classify the flow of a fluid into different regimes. These flow regimes are indicative of the dominant forces governing the fluid flow and can be categorized as follows:
- Laminar Flow: Viscous forces dominate the flow, resulting in smooth motion and less interaction between fluid layers. This type of flow is characterized by ordered, parallel streamlines.
- Transitional Flow: Fluids exhibit a mix of laminar and turbulent characteristics, making the flow regime less predictable.
- Turbulent Flow: Inertial forces dominate the flow, leading to chaotic, irregular, and energy-intensive motion. This flow is characterized by a rapid formation and dissipation of vortices, eddies, and flow instabilities.
The critical Reynolds numbers between flow regimes can vary depending on the specific geometry and conditions of the flow. For example, for circular pipe flows, experimental observations show that laminar flow occurs when Reynolds number is less than 2300 and fully turbulent flow occurs when Reynolds number is greater than 4000.

The flow regime directly impacts engineering calculations. By understanding these flow regimes and Reynolds number, engineers can optimize designs, minimize pressure losses, and ensure efficient heat transfer in fluid applications.
