Sound is a mechanical wave that propagates through a medium as a series of compressions and rarefactions. The speed of sound depends on the properties of the medium through which it travels.

In this article, we will explore the factors influencing the speed of sound in different media, as well as the methods used to measure it, and its applications in engineering.
What is the Speed of Sound
Sound is a mechanical wave that propagates through a medium. It is characterized by variations in pressure, in the form of compressions and rarefactions, creating vibrations that our ears interpret as auditory sensations.
Just like any type of wave, the velocity of sound is related to its frequency and wavelength by the following equation:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.

Where:
- v = speed of sound [m/s]
- f = frequency [Hz]
- λ = wavelength [m]
The wavelength of a wave is the distance between two consecutive points in a wave that are in phase, such as the distance between two successive peaks or troughs. Frequency, on the other hand, is the number of wave cycles that pass a given point per unit of time
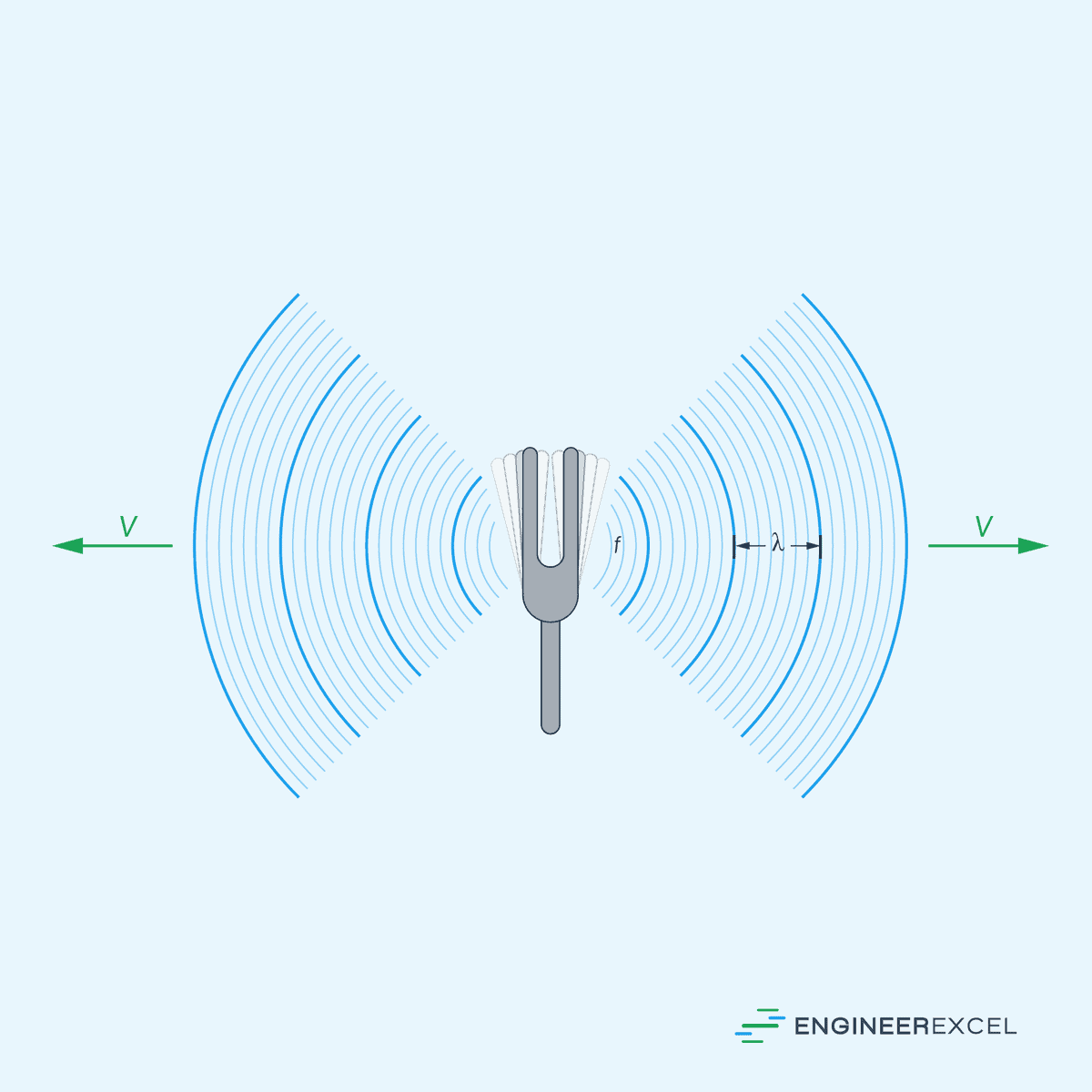
The speed of sound is not a fixed value; instead, it depends on the medium through which it travels.
Speed of Sound in Fluids
In fluids, the speed of sound depends on the bulk modulus and density, as shown by the following equation:
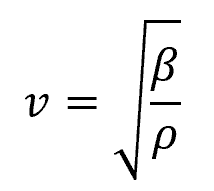
Where:
- β = bulk modulus of the fluid [Pa]
- ρ = density of the fluid [kg/m3]
The bulk modulus of a fluid is a measure of its resistance to uniform compression or volume change. It is defined as the ratio of the change in pressure to the fractional change in volume. Mathematically, it can be expressed as:
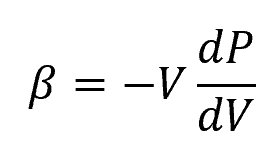
Where:
- V = volume of the fluid [m3]
- dP = change in pressure [Pa]
- dV = corresponding change in volume [m3]
In simpler terms, the bulk modulus indicates how a fluid responds to changes in pressure. As the bulk modulus increases, the speed of sound in the fluid also increases. Conversely, as density increases, the speed of sound decreases.
For an ideal gas, the formula for the speed of sound can also be written as:
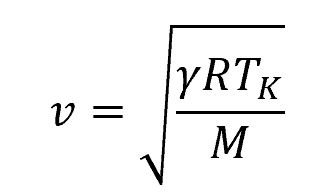
Where:
- γ = adiabatic index [unitless]
- R = gas constant [8.314 J/mol-K]
- TK = absolute temperature of the fluid [K]
- M = molecular mass of the fluid [kg/mol]
For air, a simple formula was developed to approximate the speed of sound depending on air temperature:
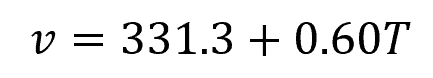
Where:
- T =air temperature [°C]
Speed of Sound in Solids
In general, sound travels faster in solids than in liquids and gases because the particles in solids are closely packed, allowing for more efficient transmission of mechanical waves. The speed of sound in a solid is determined by the elastic properties of the material, specifically its Young’s modulus (a measure of stiffness) and its density, as shown by the following equation:
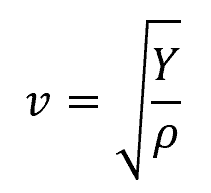
Where:
- Y = Young’s modulus of elasticity [Pa]
Speed of Sound in Different Media
To illustrate the range of the speed of sound, the table below lists its value for various media:
Measuring Speed of Sound
Resonance Tube Method
The Resonance Tube Method is a classical experimental technique used to measure the speed of sound in a gas, typically air. The apparatus consists of a long tube with one end submerged in water and the other end open to the air. A sound source (such as a tuning fork) is used to generate sound waves of known frequency, and the tube can be adjusted in height.
When the frequency of the tuning fork matches the natural frequency of the air column in the tube, a standing wave is established. This causes a resonance effect, and the height of the water column in the tube is adjusted until the maximum resonance occurs.
The fundamental frequency of the standing wave is related to the speed of sound in air and the length of the air column. By knowing the frequency of the tuning fork and measuring the corresponding length of the air column, one can use the equation v = fλ to calculate the speed of sound.
Kundt’s Tube Method
Kundt’s Tube Method is another approach used to measure the speed of sound in a gas. In Kundt’s Tube, a long horizontal glass tube is partially filled with a fine powder, such as cork dust or lycopodium powder. One end of the tube is closed, and the other end is connected to a vibrating source, typically a tuning fork.
When the tuning fork is set into vibration, it generates longitudinal sound waves that travel through the gas in the tube. The waves cause the powder particles to collect at the nodes of the standing waves, forming visible patterns known as Kundt’s nodes.
The distance between these nodes can be measured, and by knowing the frequency of the tuning fork, the wavelength of the sound wave can be determined. With the speed of sound being the product of frequency and wavelength, the experiment provides a means to calculate the speed of sound in the gas.
Pulse Echo Method
The Pulse Echo Method is a technique that can be used for measuring the speed of sound in solids, liquids, or gases. It is applied in scenarios where direct measurements using traditional methods may be challenging or impractical.
In this method, a short pulse of sound is generated and directed into the material of interest. This pulse can be created using a transducer, which converts electrical energy into mechanical vibrations.

Once the pulse encounters a boundary between different media or reaches the end of the material, it reflects back as an echo. By precisely timing the interval between the emission of the pulse and the reception of its echo, we can calculate the speed of sound in the material.
The Pulse Echo Method is widely employed in various fields, including medical imaging (ultrasound), underwater acoustics, and material testing. In medical applications, for instance, ultrasound imaging uses this method to visualize internal structures in the human body by analyzing the reflections of sound waves. The accuracy and versatility of the Pulse Echo Method make it a valuable tool for non-destructive testing and measurement of the speed of sound in different substances.
Applications in Engineering
The speed of sound plays a significant role in various engineering fields, including acoustics, aeronautics, and telecommunications.
In acoustic engineering, understanding sound propagation is essential for designing noise control systems, optimizing room acoustics, and evaluating the performance of microphones or speakers. For example, the knowledge of the speed of sound helps engineers establish the wavelength of different sound frequencies, which is vital in designing noise barriers and absorbing materials.
In aeronautical engineering, predicting and analyzing the behavior of objects moving through different mediums like air, is highly reliant on the speed of sound. Calculating the Mach number, a unit-less quantity representing the ratio of an object’s speed to the speed of sound, is critical when designing and analyzing aircraft, spacecraft, or high-speed vehicles.

In the field of telecommunications, the speed of sound is essential for determining the appropriate spacing of microphones, speakers, or underwater transducers. Signal processing techniques such as beamforming, which rely on time delays between multiple sensors, necessitate accurate knowledge of the speed of sound in various environments. In particular, underwater acoustics are important for applications like sonar and underwater communication, where the speed of sound in water substantially differs from its speed in air.
