An isothermal process is a thermodynamic process in which the temperature of a system remains constant throughout the entire process. During an isothermal process, the system exchanges heat with its surroundings in such a way that the temperature remains unchanged.

In this article, we will discuss the fundamentals and applications of isothermal processes in engineering systems, including isothermal expansion and compression, phase changes, work and heat transfer in ideal gases, and the distinction between isothermal and adiabatic processes.
What is Isothermal Process
An isothermal process is a thermodynamic process during which the temperature of a system remains constant. This implies that the heat exchange between the system and its surroundings is perfectly balanced, allowing the internal energy of the system to change without affecting its temperature.
An isothermal line on a pressure-volume diagram is represented by a curved line, as shown in the diagram below. For an ideal gas, this curve is hyperbolic in nature.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
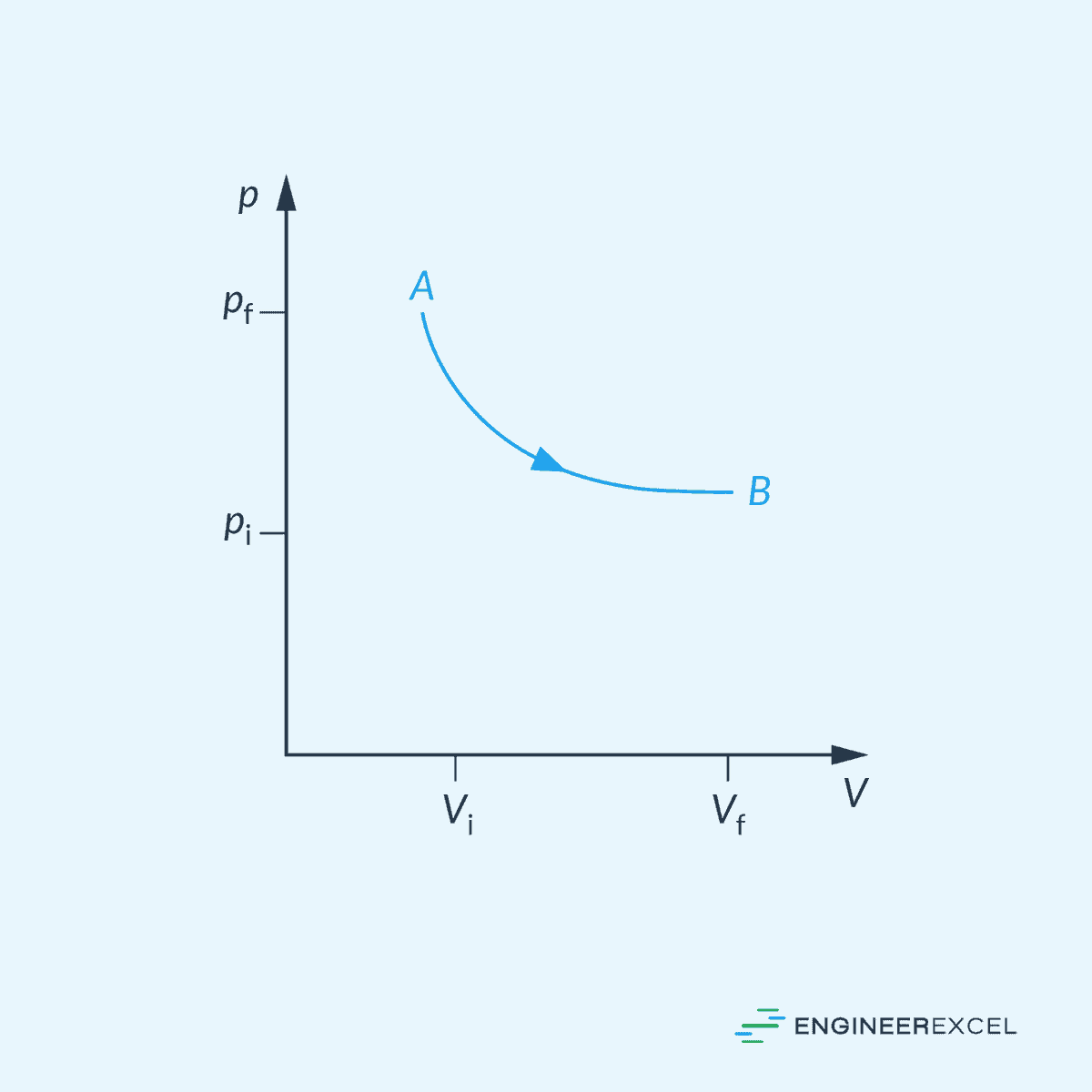
It is important to note that achieving ideal isothermal processes in reality is not possible, but it can be closely approached under specific conditions. For example, when a system is in contact with an external thermal reservoir, an isothermal process can be achieved by allowing the process to occur slowly enough to enable continuous adjustment to the reservoir’s temperature through heat exchange.
Examples of Isothermal Process
Isothermal Expansion and Compression
Isothermal expansion is the process of expanding a gas while being held at a constant temperature, and isothermal compression is the reverse process where a gas is compressed while maintaining a constant temperature. For an ideal gas, these processes can be represented by Boyle’s Law, which can be mathematically expressed as:
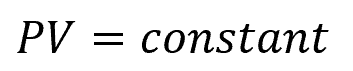
Where:
- P = pressure of the gas [Pa]
- V = volume of the gas [m3]
Boyle’s law states that the pressure of a given amount of gas is inversely proportional to its volume when the temperature is kept constant. In other words, if the volume of a gas decreases, the pressure will increase, and vice versa, as long as the temperature remains constant.
Isothermal expansion and compression find applications in various fields, including refrigeration and air conditioning systems, where these processes are utilized to control the temperature of a system while maintaining energy efficiency. Additionally, isothermal processes play a crucial role in the operation of certain types of heat engines, such as the Stirling engine, where maintaining constant temperature during expansion and compression phases enhances efficiency.
Isothermal Phase Changes
Phase changes, such as the melting or vaporization of a substance, also typically occur isothermally. The reason for this is related to the absorption or release of latent heat.
Latent heat is the heat energy that is either absorbed or released during a phase transition without a change in temperature. During the phase change, energy is used to break intermolecular forces (in the case of melting or vaporization) or to form these forces (in the case of freezing or condensation).
In the P-v diagram shown below, this is represented by the horizontal lines within the saturated liquid-vapor region.
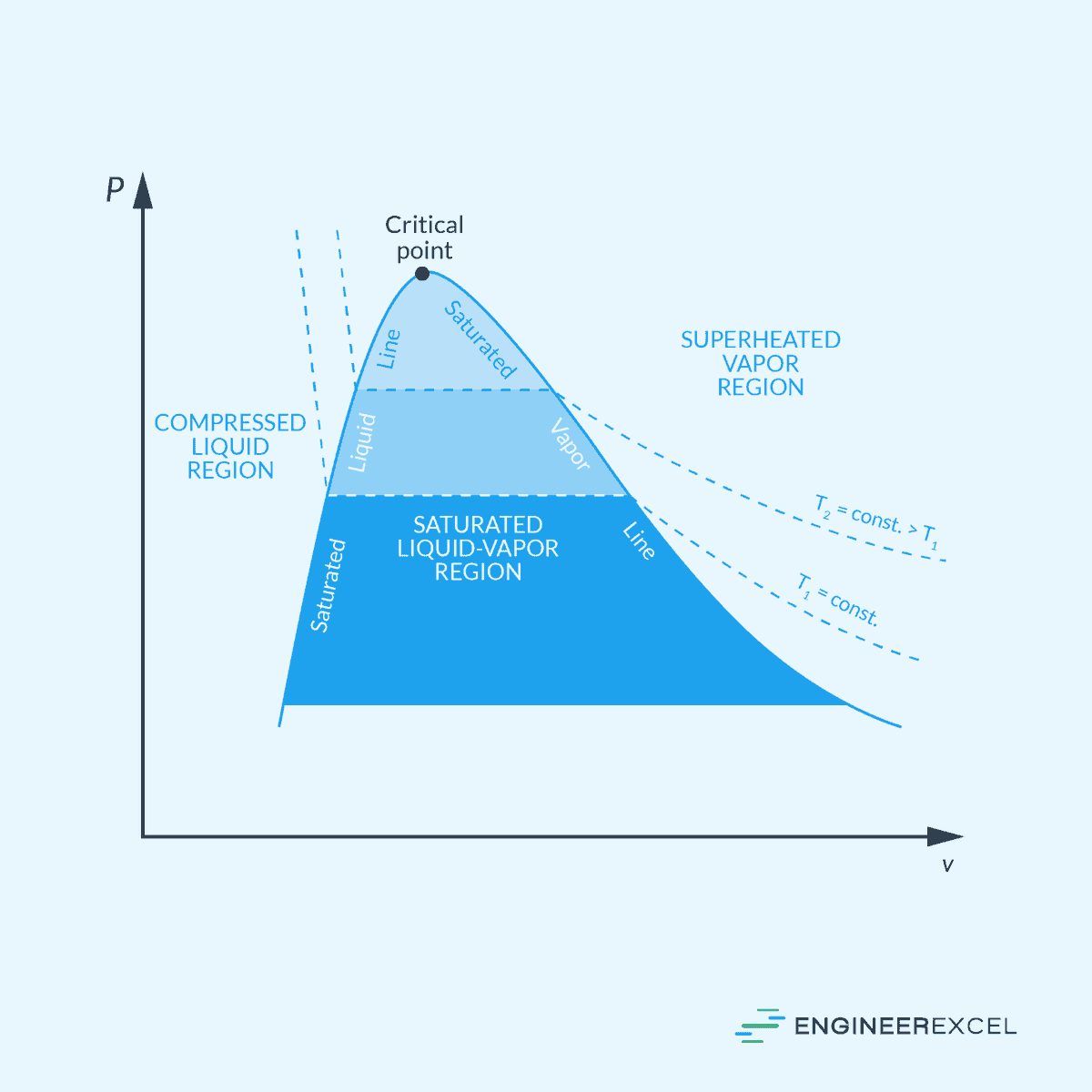
Consider the example of water turning from ice (solid) to liquid at its melting point. If you provide heat to a block of ice at 0 degrees Celsius, the heat energy is absorbed by the ice to overcome the forces holding the water molecules in a solid structure. This energy is used to break the bonds between the ice molecules and convert the substance into liquid water.
During this entire process, the temperature remains constant at 0 degrees Celsius until the entire substance has undergone the phase change. Only after all the ice has melted will any additional heat added cause an increase in temperature of the liquid water.
Isothermal Work and Heat Transfer in Ideal Gases
In ideal gases, the internal energy is proportional to temperature. Hence, during an isothermal process where the temperature is constant, there is no change in the internal energy of the gas. In this case, the first law of thermodynamics can be expressed as:
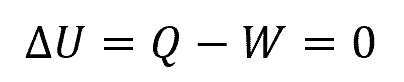
Where:
- ΔU = change in internal energy [J]
- Q = heat transferred [J]
- W = work done [J]
Therefore, in an isothermal process involving an ideal gas, all heat transferred into the system is used to do work. The work done can be calculated using the following formula:
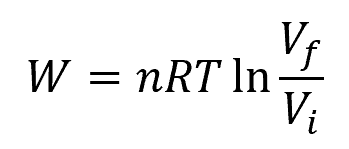
Where:
- n = number of moles of the gas [mol]
- R = universal gas constant [8.314 J/mol-K]
- T = constant temperature [K]
- Vf, Vi = final and initial volumes [m3]
Isothermal Process vs Adiabatic Process
Isothermal and adiabatic processes are two often-confused but different thermodynamic processes that describe how a system undergoes changes in its state variables, such as pressure, volume, and temperature. While both processes involve changes in energy, they differ in how heat is exchanged between the system and its surroundings.
An isothermal process is characterized by a constant temperature throughout the entire process. During an isothermal expansion or compression, the system is in thermal equilibrium with its surroundings, and heat is exchanged to maintain a constant temperature.
As mentioned above, the equation governing an isothermal process is given by:
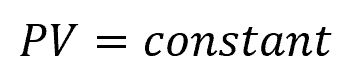
On the other hand, an adiabatic process is one in which there is no heat exchange between the system and its surroundings. In this case, any change in internal energy is solely due to work done on or by the system.
During an adiabatic expansion or compression, the system’s temperature can change because there is no heat transfer to offset the temperature variations. The equation governing an adiabatic process depends on the type of gas involved and is typically given by:
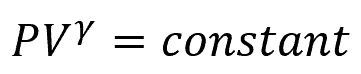
Where:
- γ = adiabatic index [unitless]
The adiabatic index, also known as the heat capacity ratio, is a thermodynamic parameter representing the ratio of the heat capacity at constant pressure to the heat capacity at constant volume of the substance.
The key distinction between isothermal and adiabatic processes lies in the heat transfer aspect. Isothermal processes involve heat exchange to maintain a constant temperature, while adiabatic processes have no heat exchange, leading to temperature changes within the system.
