The Ideal Gas Law is a fundamental concept in thermodynamics that describes the behavior of an ideal gas in terms of its pressure, volume, and temperature. It is derived from experimental gas laws and provides a useful approximation for ideal gas behavior under many experimental conditions.

In this article, we will discuss the essential principles and applications of the Ideal Gas Law.
Ideal Gas Law Explained
The Ideal Gas Law is a mathematical equation that describes the behavior of an ideal gas in terms of its pressure, volume, and temperature. It can be expressed as follows:
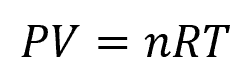

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Where:
- P = pressure of the gas [Pa or atm]
- V = volume occupied by the gas [m3 or L]
- n = number of moles of the gas [mol]
- R = universal gas constant [J/mol-K]
- T = temperature of the gas [K]
Multiple experiments have consistently demonstrated that under standard temperature (273 K) and pressure (1 atm or 101325 Pa), one mole (n = 1) of gas occupies a volume of 22.4 L. Based on this empirical evidence, the gas constant R is determined to be 8.314 J/mol-K or 0.08205 L-atm/mol-K.
The ideal gas equation is derived from various experimental gas laws, such as Boyle’s law, Charles’s law, and Avogadro’s law. These laws describe the relationships between pressure, volume, and temperature for a gas, assuming ideal behavior. In reality, gases deviate from ideal behavior at high pressures and low temperatures, but the Ideal Gas Law provides a useful approximation under many experimental conditions.
What is an Ideal Gas
An ideal gas is a theoretical concept that represents a gas with certain ideal properties. An ideal gas is comprised of particles that:
- Have a negligible volume compared to the volume occupied by the gas
- Exhibit no intermolecular forces (attraction or repulsion) between the particles
- Undergo perfectly elastic collisions with each other and the container walls
Real gases, such as air, helium, and nitrogen, can closely approximate ideal gas behavior under conditions of low pressure and high temperature. However, deviations from ideal behavior are observed when these gases are subjected to high pressures or low temperatures, due to the presence of attractive and repulsive forces between the particles.

The concept of an ideal gas serves as a foundation for understanding and predicting the behavior of real gases, and it is an integral part of kinetic theory, thermodynamics, and statistical mechanics. More accurate models, such as the van der Waals equation, can take into account deviations from ideal behavior for real gases in various conditions.
Compressibility Factor
A parameter that can be used to characterize the deviation of a real gas from ideal behavior is the compressibility factor (Z). It is defined as the ratio of the molar volume of a real gas to the molar volume of an ideal gas at the same temperature and pressure.
For an ideal gas, Z equals 1, but real gases often deviate from ideal behavior due to intermolecular forces and finite molecular sizes. A compressibility factor greater than 1 indicates that the gas occupies more space than predicted by the ideal gas law, while a value less than 1 indicates greater compressibility.
The compressibility factor is used to adjust the Ideal Gas Law to account for deviations from ideal behavior. Hence, the equation becomes:
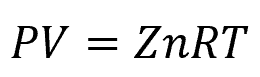
Applications of the Ideal Gas Law
The Ideal Gas Law is a fundamental equation in the study of gases and has numerous applications in various fields. Some common applications include understanding pressure, temperature, and volume relationships, calculating molecular masses, and determining gas densities.
For instance, the Gay-Lussac’s law states that the pressure of a gas is directly proportional to its temperature, provided the volume remains constant. A practical application of this law can be found in automotive tires, where an increase in temperature leads to an increase in tire pressure.
Using the Ideal Gas Law, the molecular mass of an unknown gas can also be calculated from a known amount, volume, pressure, and temperature. For example, knowing the molecular mass of a gas is important in chemical reaction stoichiometry, where balanced equations require the correct ratio of moles for reactants and products.
Lastly, the Ideal Gas Law can be rearranged to find the densities of various gases under different conditions. This relationship is essential in applications like predicting the behavior of gases in the atmosphere.
