Newtonian fluids are characterized by a linear relationship between shear stress and shear rate, following Newton’s law of viscosity. In these fluids, viscosity remains constant regardless of the applied stress, making their flow behavior relatively predictable.

In this article, we will discuss the characteristics of Newtonian fluids, including examples of Newtonian fluids and comparison with non-Newtonian fluids.
What is Newtonian Fluid
A Newtonian fluid is a type of fluid that exhibits a linear relationship between its shear stress and shear rate. This means that the fluid’s resistance to deformation is constant, regardless of the applied force. This property makes Newtonian fluids predictable and easy to analyze, as they follow Newton’s law of viscosity.
In mathematical terms, the behavior of a Newtonian fluid can be described by the equation:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.

Where:
- τ = shear stress applied to the fluid [Pa]
- μ = fluid’s viscosity [Pa-s]
- du/dy = shear rate, representing the fluid’s velocity gradient [s-1]
This equation was first used by Isaac Newton to postulate the relation between the shear strain rate and shear stress for such fluids.
For a Newtonian fluid, viscosity is a constant value, independent of the shear rate. This constant viscosity makes them simple to model and understand in many engineering applications, such as fluid dynamics and lubrication systems.
Examples of Newtonian Fluids
Newtonian fluids are the simplest mathematical models of fluids that incorporate viscosity. Although no actual fluid conforms precisely to this definition, there are common liquids and gases that can be reasonably treated as Newtonian for practical calculations in engineering.
Newtonian fluids are characterized by a constant viscosity regardless of the shear rate applied to them. In classical Newtonian fluids, this behavior is attributed to small isotropic molecules that do not orient themselves in response to flow.

However, it is also possible to observe Newtonian behavior in systems with large anisotropic molecules, such as low-concentration protein or polymer solutions. Anisotropic molecules have different properties along different axes, and in some cases, their behavior may mimic that of classical Newtonian fluids.
Water is perhaps the most familiar example of a Newtonian fluid, and it exhibits a constant viscosity over a wide range of shear rates. However, its viscosity does change with temperature: as temperature increases, water viscosity decreases. Additionally, the constant viscosity of water under varying shear rates is one of the reasons why it is often the standard fluid for comparing the flow properties of other liquids.
Air and other gases are also examples of Newtonian fluids. Just like water, the viscosity of gases changes with temperature. The compressibility of gases, however, impacts their behavior when under pressure. Gases are essential in processes like pneumatic systems and combustion engines, where their viscosity directly affects the efficiency and performance of the system.
Glycerol is another example of a Newtonian fluid and has a higher viscosity than water. It is widely used as a solvent, antifreeze, and a lubricant due its unique chemical properties and stability. Glycerol’s Newtonian behavior enables it to be easily managed and manipulated in various chemical and industrial applications, and it is often used as a reference fluid in rheological studies.
Oil may be Newtonian, depending on its composition and additives. For instance, simple mineral oils are Newtonian fluids, while some motor oils exhibit non-Newtonian behavior due to the presence of viscosity modifiers. The correct choice of oil is important for machinery and vehicle performance, as the oil’s viscosity influences friction, wear, and heat generation.
Newtonian vs Non-Newtonian Fluids
It is important to note that not all fluids are Newtonian. Some fluids exhibit properties known as non-Newtonian behavior.
Unlike Newtonian fluids, which maintain a constant viscosity regardless of shear rate, force, or time, non-Newtonian fluids exhibit variable viscosity dependent on these factors. Examples of non-Newtonian fluids include ketchup, blood, and yogurt.
Non-Newtonian fluids can be further categorized into several types:
- Pseudoplastic: Fluids whose viscosity decreases as the shear rate increases. These are also known as shear-thinning fluids. An example is paint.
- Dilatant: Fluids whose viscosity increases as the shear rate increases. These are also known as shear-thickening fluids. An example is quicksand.
- Bingham Plastics: Fluids that only start to flow after the critical shear stress is reached. An example is mustard.
Newtonian Fluid in Power Law Model
The Power Law model is commonly used to describe the behavior of non-Newtonian fluids under certain flow conditions. However, it is important to understand how Newtonian fluids relate to this model.
In the Power Law model, the relationship between shear stress (τ) and shear rate (γ̇) is defined as follows:
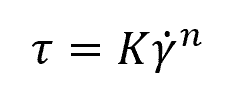
Where:
- K = flow consistency index [Pa-sn]
- γ̇ = shear rate [s-1]
- n = flow behavior index [unitless]
The flow consistency index in the power-law fluid model represents the consistency or thickness of a fluid. It is a measure of how easily a fluid deforms under applied stress. A higher flow consistency index indicates a more viscous or thicker fluid, while a lower value signifies a more easily flowing or thinner fluid.
The flow behavior index (n), on the other hand, characterizes the non-Newtonian behavior of a fluid. It reflects the degree of shear-thinning or shear-thickening exhibited by the fluid. Values below or above 1 signify shear-thinning or shear-thickening behavior, respectively.
For a Newtonian fluid, the flow behavior index is equal to 1. Thus, the equation simplifies to:
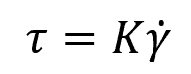
This relationship indicates that the shear stress is directly proportional to the shear rate for a Newtonian fluid, and the proportionality constant (K) represents the constant viscosity (μ) for the fluid. This is illustrated in the diagram below.
The velocity field of Newtonian fluids can also be studied in the context of Power Law fluids. In a fully developed pipe flow, the Poiseuille flow of a power-law fluid can be analyzed. For Newtonian fluids, this simplifies to the well-known Hagen-Poiseuille flow.
