Vapor pressure is the pressure exerted by a vapor in thermodynamic equilibrium with its condensed phases. It represents the tendency of molecules in a substance to escape into the gaseous phase and is influenced by factors such as temperature and the nature of the substance.

In this article, we will discuss vapor pressure in detail, including the factors affecting it, its calculation, and its practical applications in engineering.
What is Vapor Pressure
Vapor pressure is a concept in thermodynamics describing the pressure exerted by a vapor that is in equilibrium with its condensed phases within a closed container. This pressure arises due to the natural tendency of liquids and solids to evaporate or sublime into a gaseous form, as well as the propensity of gases to condense back into their liquid or solid states.
In a closed container, there is a continual exchange of molecules between liquid (or solid) and its gaseous phase. Some particles within the liquid, regardless of temperature, possess enough energy to overcome the intrinsic cohesive forces and enter the gaseous phase. The vapor pressure of a substance is a measure of the pressure the gaseous component of the substance applies on its container.
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.

An equilibrium state is established between the liquid and its gaseous phase when the rate of condensation of the gas molecules becomes equal to the rate of evaporation of the liquid or solid. As a result, the amount of each phase within the container will no longer change, and the gas is said to be in equilibrium with the liquid or solid.
It is important to note that, while surface area of the solid or liquid may affect the rate at which molecules transition between the phases, it does not alter the equilibrium vapor pressure.
Factors Affecting Vapor Pressure
Intermolecular Forces
A significant factor affecting vapor pressure is the strength of intermolecular forces within the liquid. Liquids with strong intermolecular forces, such as hydrogen bonding or dipole-dipole interactions, typically exhibit lower vapor pressures. Conversely, liquids with weak intermolecular forces, such as those primarily governed by dispersion (or London) forces, generally have higher vapor pressures.
Temperature
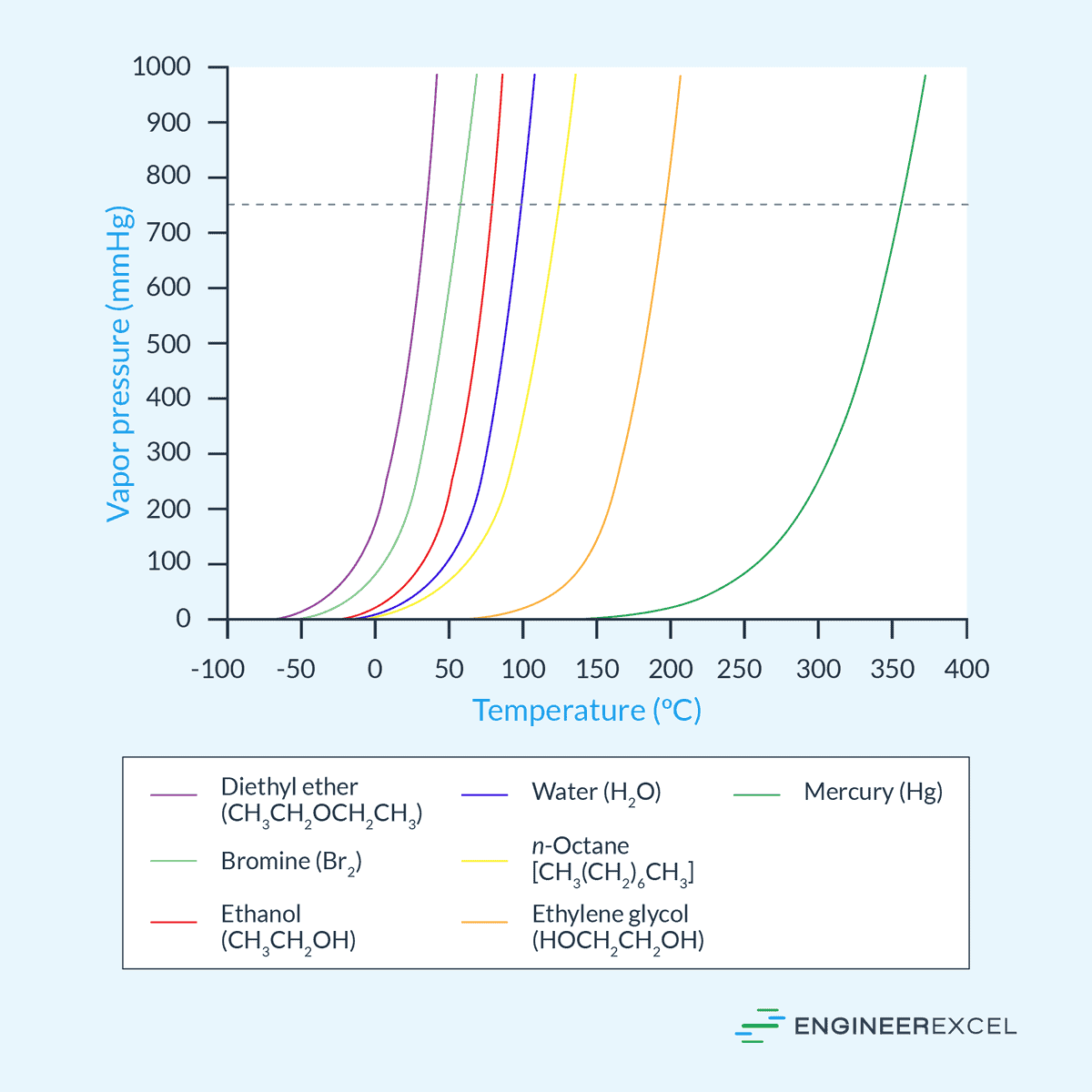
Another important factor that affects vapor pressure is temperature. As temperature increases, the kinetic energy of the molecules within the liquid increases, resulting in a greater number of molecules transitioning to the vapor phase. This increase in vaporization consequently leads to higher vapor pressures.
To illustrate this relationship, the vapor pressure vs temperature curves of different fluids are shown in the diagram below.
Clausius-Clapeyron Equation
The relationship between temperature and vapor pressure is typically represented by the Clausius-Clapeyron equation:
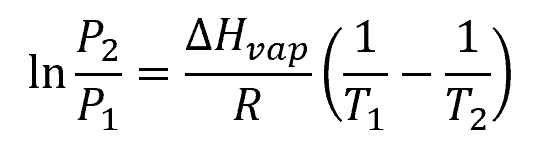
Where:
- T1 and T2 = different temperature points [K]
- P1 and P2 = corresponding vapor pressures at T1 and T2 [Pa]
- ΔHvap = enthalpy of vaporization [J/mol]
- R = gas constant [8.314 J/mol-K]
This equation enables us to estimate the vapor pressure at a different temperature when the vapor pressure at a specific temperature and the enthalpy of vaporization are known.
Vapor Pressure of Solutions
When a solute is added to a solvent to form a solution, the vapor pressure of the solution can be different from that of the pure solvent. In this case, the vapor pressure of a solution can be obtained using Raoult’s Law and Dalton’s Law.
Raoult’s Law states that the partial pressure of each component in an ideal liquid mixture equals the vapor pressure of the pure component multiplied by its mole fraction in the mixture. When two or mroe volatile liquids A and B are mixed to form a solution, the vapor phase comprises both components. Once the solution reaches equilibrium, the total vapor pressure can be calculated by combining Raoult’s law with Dalton’s law of partial pressures, resulting in the following equation.
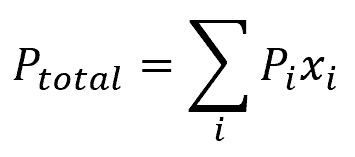
Where:
- Ptotal = total pressure of the solution [Pa]
- Pi = partial vapor pressure of one component [Pa]
- xi = mole fraction of one component [unitless]
- i = number of components in the solution [unitless]
Practical Applications
Distillation
Distillation is a widely used separation technique in industries such as the production of chemicals, petroleum, and alcoholic beverages. This process relies on the differences in vapor pressure of the various components in a mixture in order to separate the components.
By increasing temperature, the component with a higher vapor pressure is more likely to vaporize, leaving the remaining mixture enriched with the less volatile component. This process is repeated in stages to achieve the desired level of separation.
Refrigeration
The principles of vapor pressure are essential in refrigeration systems. Refrigerants are substances that can change phase rapidly, absorbing and releasing heat in the process. A refrigeration cycle operates by manipulating the vapor pressure and temperature of the refrigerant, resulting in the desired cooling effect.
Relief Devices
Relief devices, such as rupture disks and pressure relief valves, must be correctly sized to protect against excessive pressure buildup. This involves accurate vapor pressure calculations for the chemicals being processed, as well as environmental conditions and potential overpressure scenarios.
