Non-Newtonian fluids are substances that do not follow classical Newtonian viscosity behavior. This means that their viscosity can change in response to applied stress or strain.

This article explores their classifications, applications in various industries, and mathematical models used to describe the behavior of non-Newtonian fluids.
What are Non-Newtonian Fluids
Newton’s law of viscosity states that the shear stress acting on a fluid is proportional to its shear rate, as shown in the following equation:
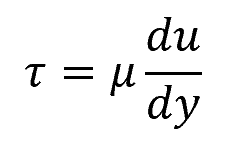
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Where:
- τ = shear stress [Pa]
- μ = viscosity of the fluid [Pa-s]
- du/dy = shear rate [s-1]
Non-Newtonian fluids are a class of fluids that do not follow this rule. In these fluids, the relationship between shear stress and shear rate is nonlinear, as shown in the diagram below.
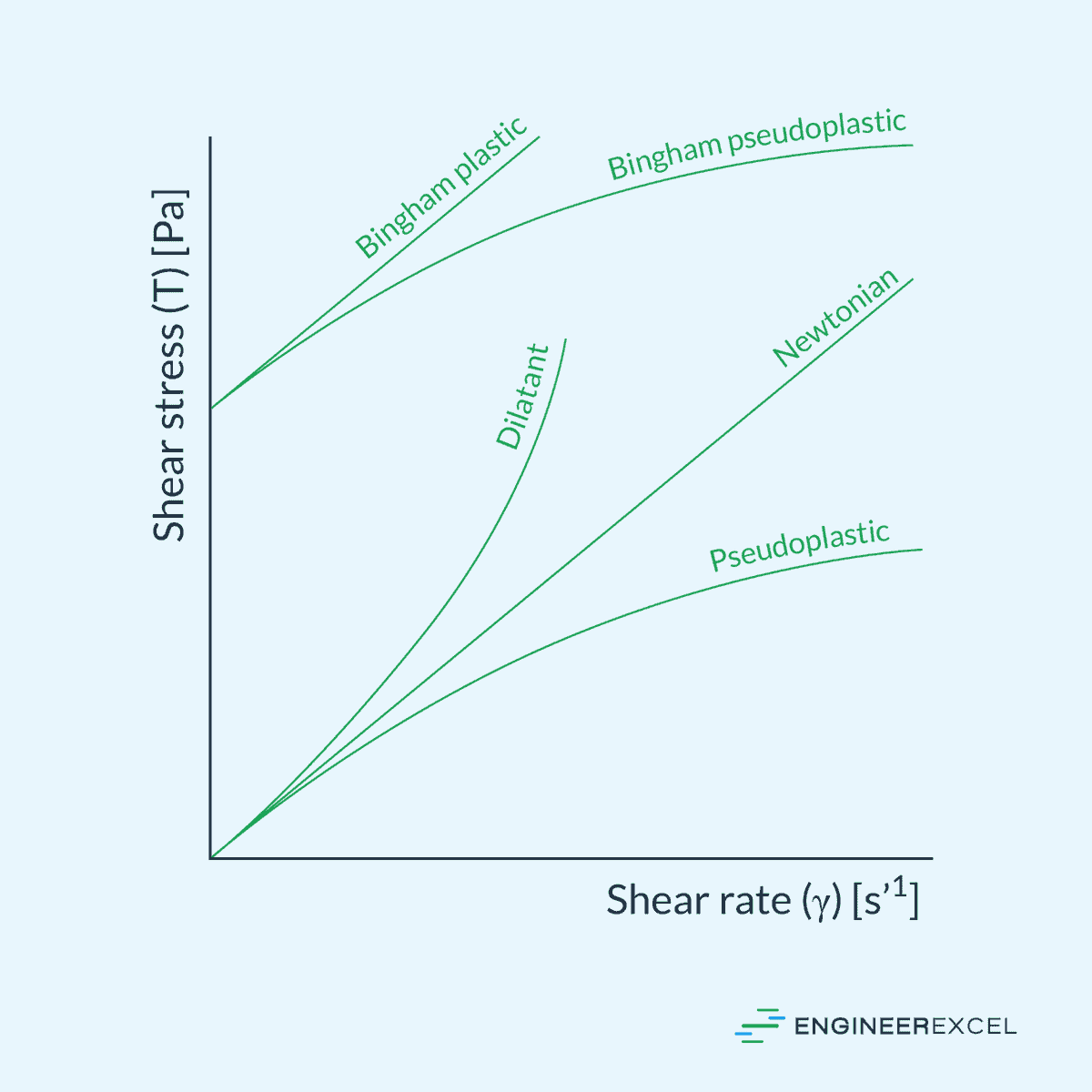
Unlike Newtonian fluids, the viscosity of non-Newtonian fluids varies with the magnitude and duration of the applied force. These fluids exhibit a diverse range of behaviors, and their viscosity can be dependent on factors such as shear rate, stress, or time. This departure from Newtonian behavior is often attributed to the microstructural elements within the fluid, such as polymers, particles, or other additives, which interact and influence the flow characteristics.
This dynamic and adaptive response sets non-Newtonian fluids apart from Newtonian fluids, providing unique properties that find applications in various industries. However, their complex behavior poses unique challenges when analyzing their flow in engineering applications. Thus, understanding and manipulating the rheological properties of non-Newtonian fluids is important in optimizing processes and developing innovative technologies.
Types of Non-Newtonian Fluids
Non-Newtonian fluids can be classified into different categories based on their behavior. These are illustrated in the diagram below.
Power Law Fluids
These fluids show a power-law relationship between shear stress and shear rate. They are further subdivided into two types: pseudoplastic (shear thinning) and dilatant (shear thickening).
Pseudoplastic Fluids
Pseudoplastic fluids are fluids whose viscosity decreases as shear rate increases, causing shear rate thinning. This behavior is observed in fluids like polymer solutions and blood.
Dilatant Fluids
Dilatant fluids are fluids whose viscosity increases as shear rate increases, resulting in shear rate thickening. Examples include cornstarch mixed in water and quicksand.
Bingham Plastics
Bingham fluids exhibit a minimum shear stress known as yield stress that must be surpassed before the fluid begins to flow. This behavior is common in materials like toothpaste and mayonnaise. Once the yield stress is exceeded, they act similar to Newtonian fluids, maintaining a linear relation between additional shear stress and the corresponding strain rate.
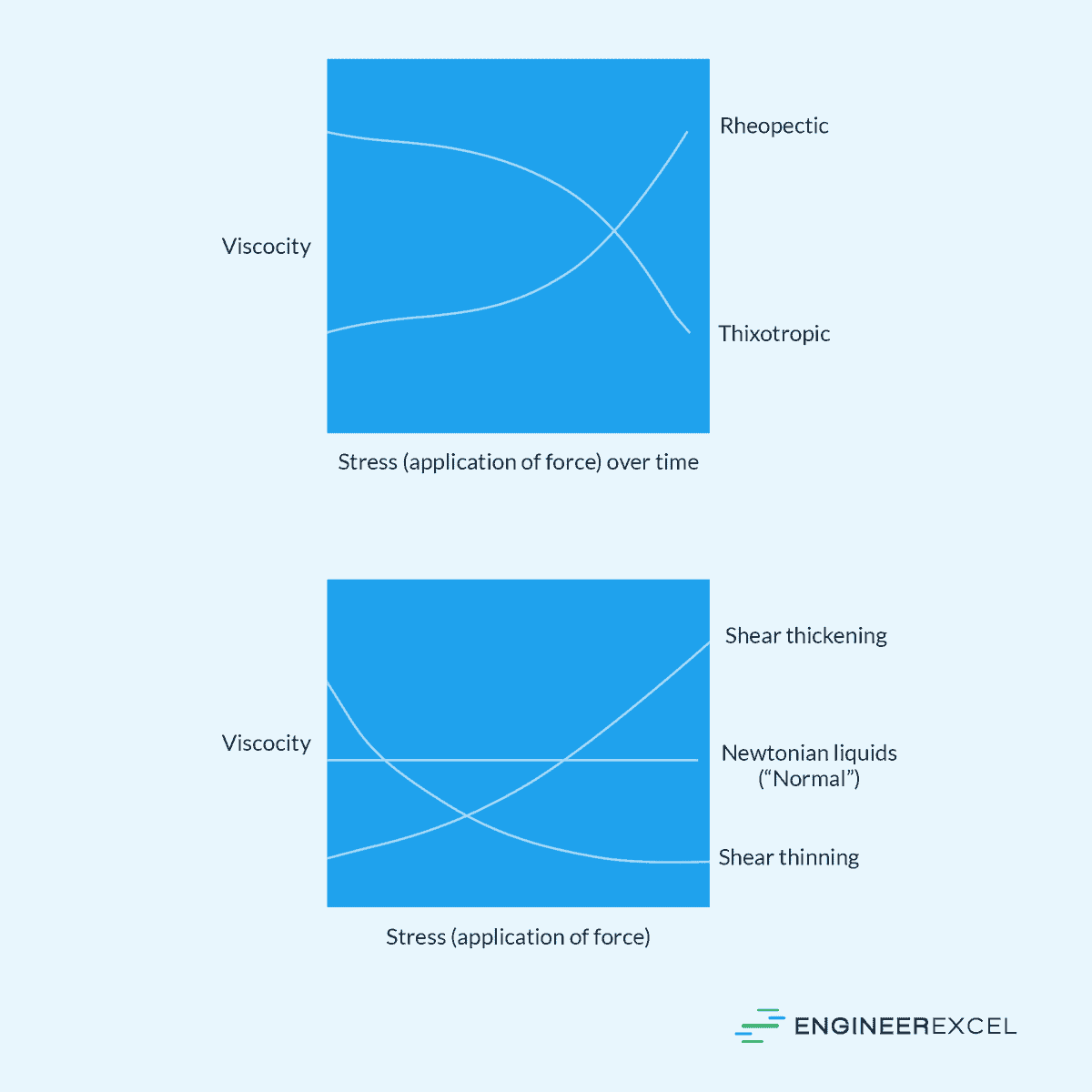
Thixotropic Fluids
Thixotropic fluids exhibit a decrease in viscosity with time when an applied shear stress is constant. This change in viscosity is reversible, and the material recovers its original viscosity when the stress is removed. Thixotropic fluids include ketchup and certain paints.
Rheopectic Fluids
These fluids show an increase in viscosity with time when a constant shear stress is applied. Their behavior is opposite to thixotropic fluids. However, this type of non-Newtonian behavior is quite rare and less studied.
Applications of Non-Newtonian Fluids
Some of the prominent applications of non-Newtonian fluids include consumer goods, automotive, and biomedical engineering.
In the consumer goods industry, non-Newtonian fluids are used in numerous products due to their unique flow properties. For example, toothpaste exhibits pseudoplastic behavior, allowing it to flow easily when pressure is applied but maintain its shape on the brush. Similarly, ketchup exhibits shear thinning and thixotropic behavior, making it easier to pour from a bottle when shaken.

The automotive industry also benefits from the unique properties of non-Newtonian fluids. For instance, in shock absorbers and dampers, magnetorheological (MR) fluids – whose viscosity can be controlled by a magnetic field – are employed to improve vehicle handling and comfort. The high shear rates generated by turbulent flow cause these fluids to thicken, providing a more significant damping force when needed.
In biomedical engineering, non-Newtonian fluids are used in developing artificial blood and biomimetic materials. Blood itself is a non-Newtonian fluid, with its viscosity depending on the shear rate and hematocrit (the volume fraction of red blood cells). This behavior is important for understanding blood flow dynamics and the design of prosthetic devices, such as heart valves and blood pumps.
Researchers are also investigating the use of non-Newtonian fluids, like hydrogels, for creating bio-inspired materials with unique mechanical properties for tissue engineering and drug delivery systems.
Mathematical Models of Non-Newtonian Fluids
Non-Newtonian fluids exhibit complex rheological behavior. Hence, several mathematical models have been proposed to describe their characteristics more accurately. This section covers some of the most widely-used models, including the Power Law Model, Bingham Plastic Model, Herschel-Bulkley Model, and Casson Model.
Power Law Model
The Power Law Model is one of the simplest constitutive equations for non-Newtonian fluids. Known as the Ostwald-de Waele relationship, it is given by:
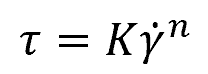
Where:
- K = flow consistency index [Pa-sn]
- γ̇ = shear rate [s-1]
- n = flow behavior index [unitless]
For n < 1, the fluid exhibits shear-thinning behavior, while n > 1 indicates shear-thickening behavior. A Newtonian fluid has n = 1 and K equals the dynamic viscosity.
Bingham Plastic Model
The Bingham Plastic Model describes fluids that exhibit an initial resistance to flow, also known as a yield stress. Mathematically, the Bingham plastic is represented as follows:

Where:
- τo = yield stress [Pa]
Below the yield stress, the material behaves as a solid, and above the yield stress, it flows like a viscous fluid. The model is applicable to fluids like toothpaste, paint, and drilling mud.
Herschel-Bulkley Model
The Herschel-Bulkley Model is an extension of the Bingham Plastic and Power Law models to cover shear-thinning or shear-thickening behavior. The equation for this model is:
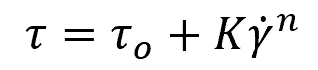
This model is useful to describe the flow behavior of materials that don’t start flowing until a certain stress (yield stress) is exceeded, and the flow behavior after yielding can be described by a power-law relationship.
Casson Model
The Casson Model is another important rheological model, which utilizes the square root of shear stress in its equation:
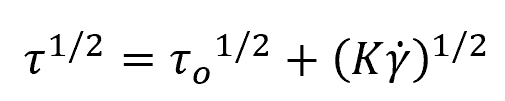
This model is often applied to suspensions with large particle sizes or high concentrations, such as blood, chocolate, and certain inks.
It is important to note that aside from the models mentioned here, there are several other models that can be used to describe non-Newtonian behavior. Choosing a rheological model that best represents the behavior of the specific material under consideration is important, as different models are applicable to different types of fluids and deformation conditions.
