An incompressible fluid is a substance that exhibits negligible changes in density under the influence of external pressure. In fluid mechanics, the assumption of incompressibility simplifies fluid equations and makes the analysis more manageable for a wide range of engineering applications.

In this article, we will discuss the fundamental concepts and dynamics of incompressible fluids, including the Mach number, continuity equation, and Bernoulli’s equation.
What is Incompressible Fluid
An incompressible fluid is a fluid whose density remains constant under the application of external forces, such as pressure or temperature changes. In other words, when an incompressible fluid is subjected to compression, its volume does not change.
While all fluids possess some level of compressibility, it is acceptable to assume that a fluid is incompressible as long as its density changes negligibly during the flow process. In general, liquids are often considered incompressible for many engineering applications because the changes in their density are usually negligible compared to gases.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Water, for example, is commonly treated as an incompressible fluid for various calculations in fields like fluid mechanics, hydrodynamics, and engineering, where changes in volume due to pressure variations are often considered minimal.
The density of water at atmospheric pressure is 1000 kg/m3. When the pressure is multiplied by a factor of 200, the density increases to 1010 kg/m3. Since increasing the pressure by a factor of 200 only raises the density by 1%, it is acceptable to consider water as an incompressible fluid.
Mathematically, the density of an incompressible fluid is assumed to be constant in calculations, simplifying equations and making the analysis of fluid flow more manageable.
Mach Number
In fluid mechanics, it is generally reasonable to consider all liquids as incompressible fluids. The only instance where it is necessary to consider the changes in density of liquids is when sound propagation effects need to be considered.
However, it can also be acceptable to treat gases as incompressible. This is particularly true in situations where there are minimal changes in velocity and pressure, and if the speed of the flow is low. In practice, this criterion can be gauged using a dimensionless parameter called the Mach number.
The Mach number (Ma) represents the ratio of the speed of a fluid to the speed of sound in the surrounding medium. Mathematically, it is expressed as:
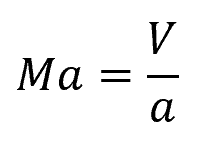
Where:
- Ma = Mach number [unitless]
- V = velocity of the fluid [m/s]
- a = speed of sound in the fluid [m/s]
When an object is traveling at the speed of sound, the Mach number is equal to 1. If the Mach number is greater than 1, the object is traveling faster than the speed of sound and is said to be supersonic. If the Mach number is less than 1, the object is traveling slower than the speed of sound and is referred to as subsonic.
In many engineering applications, a Mach number less than 0.3 is often used as a threshold to consider the flow as incompressible. However, it is important to note that this threshold is somewhat arbitrary and may vary depending on the specific application.
Dynamics of Incompressible Fluids
In fluid flow analysis, four fundamental equations are employed to describe the general behavior of fluids: the continuity equation, momentum equation, energy equation, and equation of state. However, when dealing with incompressible fluids where the density is constant, the energy equation becomes uncoupled and the equation of state simplifies to the statement that density is nearly constant. As a result, analyzing incompressible flow only necessitates continuity and momentum analysis.
Continuity Equation
The continuity equation describes the conservation of mass within a fluid flow. It states that the rate of mass entering a control volume must be equal to the rate of mass exiting the same volume, as shown in the diagram below.
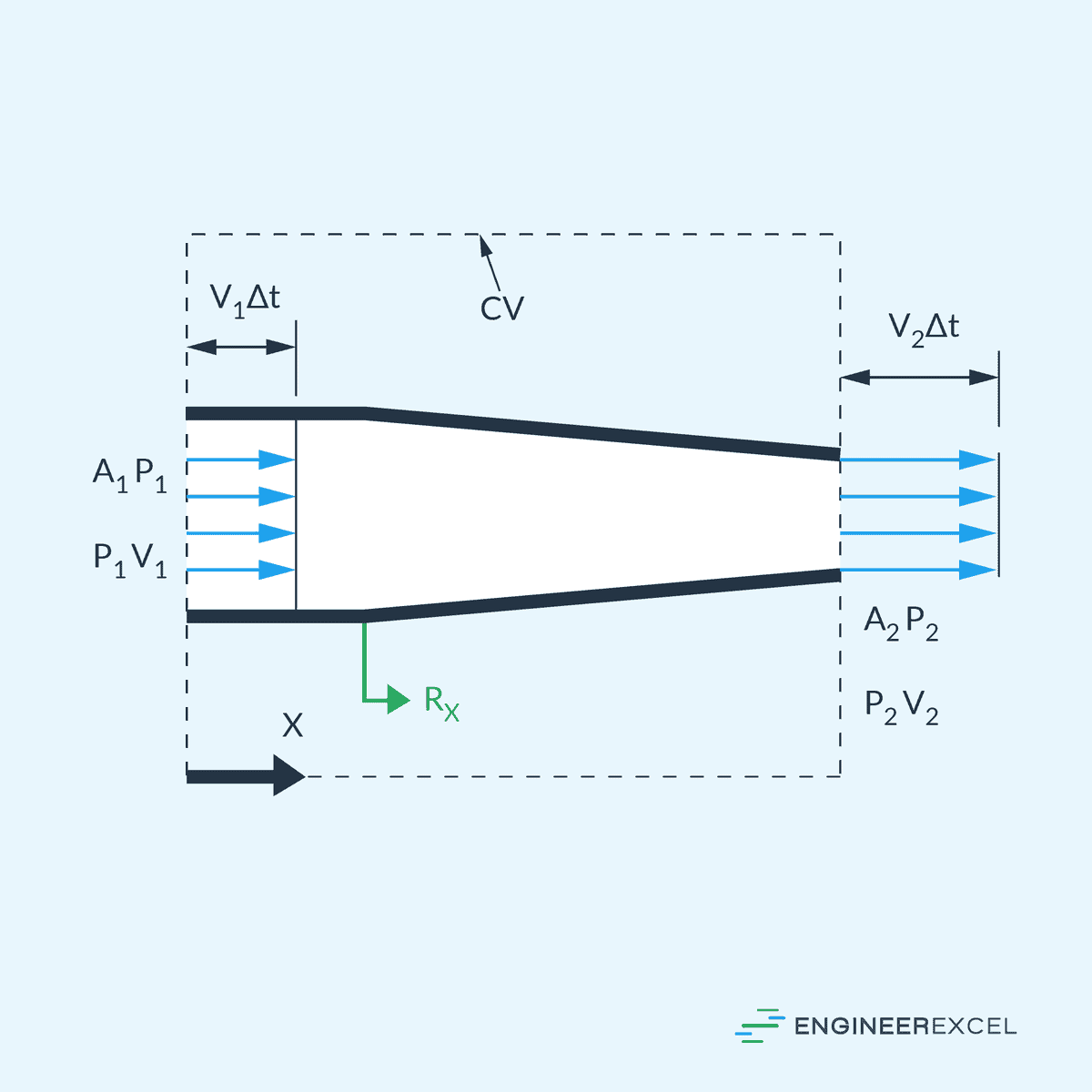
In general, the continuity equation for a steady, one-dimensional flow can be expressed as:
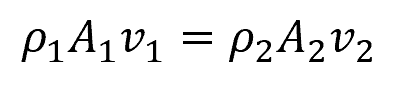
Where:
- ρ1, ρ2 = fluid density at two different points along the flow [kg/m3]
- A1, A2 = cross-sectional area of the flow at the two points [m2]
- v1, v2 = flow velocity at the two points [m/s]
However, since density is constant for incompressible fluids, the continuity equation reduces to:
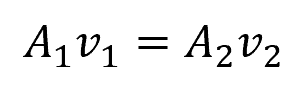
This principle is widely used in fluid mechanics and is applied in various engineering applications, such as the design of pipelines, nozzles, and diffusers. It helps in understanding and predicting how fluid flow characteristics change as it moves through different sections with varying cross-sectional areas and velocities.
Bernoulli’s Equation
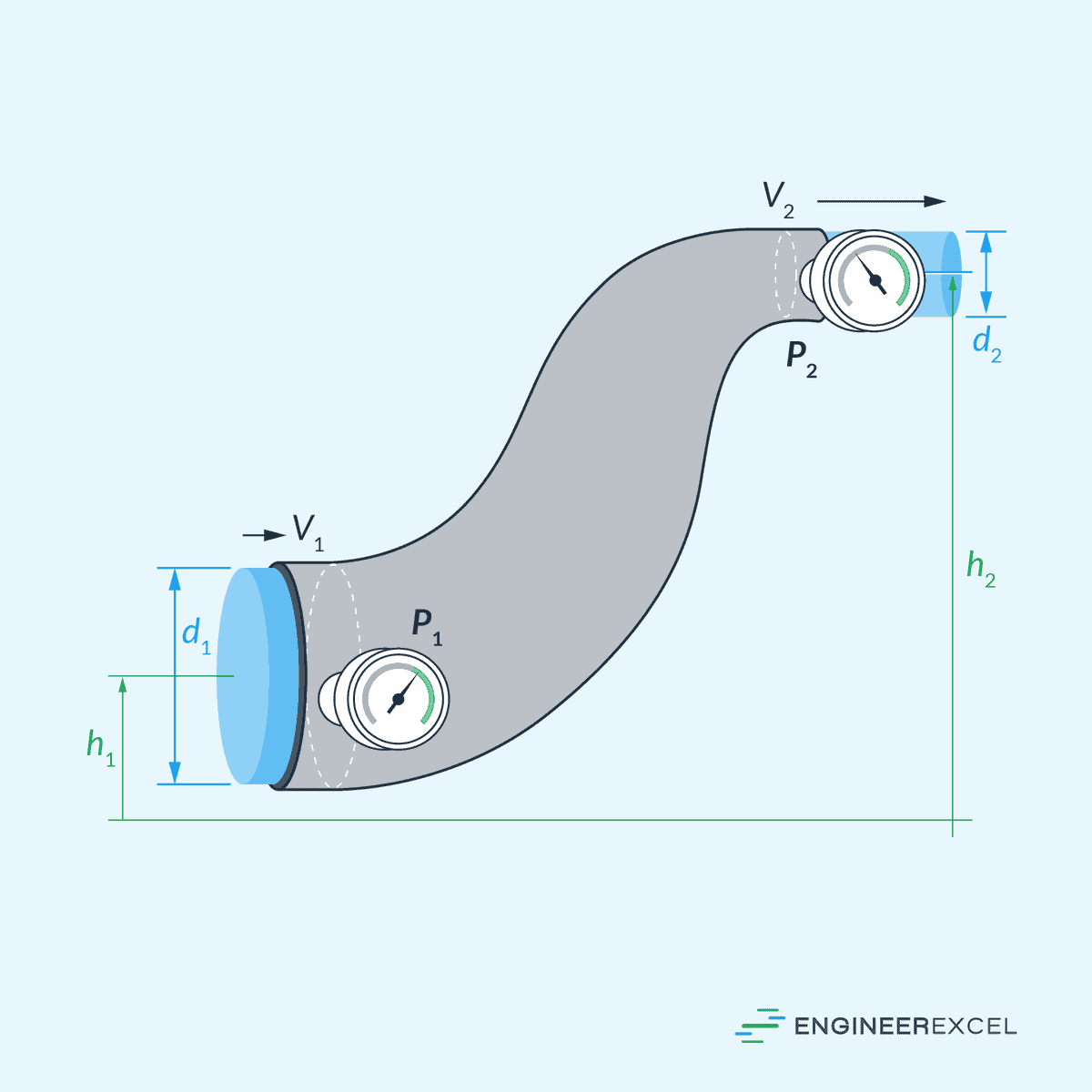
Another fundamental equation used to describe the flow of incompressible fluids is the Bernoulli Equation. It is a simplified form of the momentum equation, relating pressure, kinetic energy, and potential energy for an incompressible fluid flowing along a streamline, as shown in the diagram below.
Mathematically, Bernoulli’s equation can be expressed as:
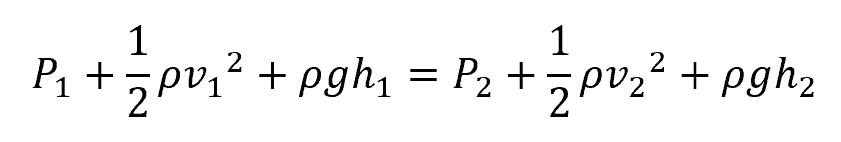
Where:
- P1, P2 = pressure at two different points along the flow [Pa]
- h1, h2 = elevation at the two points [m]
- g = gravitational acceleration [9.81 m/s2]
Bernoulli’s equation assumes steady, incompressible, and inviscid fluid flow, and disregards any external forces like viscous forces or turbulence. This equation is applicable along a single streamline, but it can be applied between two points on different streamlines if the flow is irrotational.
