Viscosity measures a fluid’s resistance to flow. There are two types of viscosity: dynamic viscosity and kinematic viscosity. In this article, we will discuss the differences between the two, the factors affecting viscosity, and various methods for measuring dynamic and kinematic viscosities.
Dynamic Viscosity vs Kinematic Viscosity
Viscosity is a fundamental property of fluids that measures their resistance to flow. It is categorized into two types: dynamic viscosity and kinematic viscosity.
Dynamic viscosity (μ), also known as absolute viscosity or coefficient of viscosity, is defined as the tangential force per unit area required to maintain a unit velocity gradient between two parallel layers of fluid. This is mathematically expressed as:

Where:
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
- μ = dynamic viscosity [Pa-s]
- τ = shear stress between the fluid layers [Pa]
- du/dy = fluid velocity gradient [s-1]
The SI unit for dynamic viscosity is Pascal seconds (Pa·s). However, it is also commonly represented in centipoise (cP) where 1 Pa·s = 1000 cP.
The dynamic viscosity of water at room temperature is approximately 1 cP. Hence, viscosity in centipoise is an indication of viscosity relative to that of water at room temperature.
On the other hand, kinematic viscosity (ν) is defined as the ratio of dynamic viscosity to fluid density, as shown by the following formula:
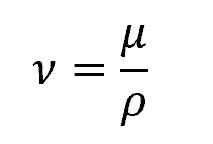
Where:
- ν = kinematic viscosity [m2/s]
- ρ = fluid density [kg/m3]
It is termed kinematic because the mass units cancel out, meaning that force is not a factor, leaving only the length and time dimensions. The SI unit for kinematic viscosity is square meters per second (m²/s), but it is also commonly expressed in Stokes where 1 St = 10-4 m2/s
Factors Affecting Viscosity
Temperature
Temperature has a significant effect on both the dynamic and kinematic viscosities of fluids. For liquids, as the temperature increases, the viscosity typically decreases. This can be explained by the fact that at higher temperatures, the molecules have more energy and move more rapidly, resulting in decreased intermolecular forces and lower viscosity.
In contrast, gases generally exhibit an increased viscosity with increasing temperature, since the intermolecular forces are weaker, and increased temperature leads to more frequent collisions between the molecules.
Pressure
The absolute viscosity of most fluids remains largely unaffected by pressure within the typical range of engineering applications. In contrast, kinematic viscosity exhibits significant variation in response to pressure, as it is influenced by fluid density. However, this relationship is not as straightforward as with temperature, and the effects of pressure may vary according to the specific fluid and its properties.
Fluid Composition
The composition of a fluid also has a significant impact on its viscosity. Mixtures of different fluids, such as oil and water, can exhibit a wide variety of viscosities depending on the proportions of each component.

Additionally, the presence of additives or contaminants in a fluid can alter its viscosity. For instance, some industrial processes and applications require the use of viscosity-enhancing additives to modify the fluid properties and achieve desired performance.
Measuring Dynamic and Kinematic Viscosities
There are various methods to measure fluid viscosity, depending on the type of fluid and the required accuracy. In general, dynamic viscosity is measured by observing the fluid’s resistance to flow under an external, controlled force, while kinematic viscosity is measured by observing the fluid’s resistance to flow under the force of gravity.
In order to understand the differences in measurement techniques, it is important to discuss various types of viscometers that can be employed for measuring dynamic and kinematic viscosities.
Capillary (Glass) Viscometer Test
The capillary viscometer test uses a glass tube, referred to as a U-tube, which is submerged in a temperature-controlled bath. The fluid is allowed to flow within the tube from one marked point to another through suction or the force of gravity, and the time it takes is measured. This measured time is then multiplied by a constant to calculate either absolute viscosity (suction) or kinematic viscosity (force of gravity).

ASTM D445 specifies a procedure for the determination of the kinematic viscosity of liquid petroleum products using a glass capillary viscometer.
Rotational Viscometer Test
Rotational viscometers involve a rotating apparatus, called a spindle, that is submerged within the fluid. The torque on the shaft is used to measure the fluid’s resistance to flow. Since this method accounts for the fluid’s internal shear stress, rotational viscometers calculate absolute viscosity.
A more advanced version of this apparatus is the Stabinger viscometer, which uses a modified standalone floating spindle controlled by electromagnetic forces, eliminating the need to factor in bearing friction.
Falling Ball and Falling Piston Viscometer Tests
In falling ball and falling piston viscometers, a ball or piston falls into the fluid, and the time is measured between the passing from one marked point to another. The terminal velocity, size, and density of the ball or piston are then used to calculate viscosity using Stokes’ law.
