In fluid mechanics, shear strain rate refers to the rate at which adjacent fluid layers deform relative to each other due to shear stress. It is a measure of the change in velocity gradient within the fluid, representing the fluid’s tendency to undergo shear deformation. In this article, we will discuss the definition and significance of shear strain rate in fluid mechanics, including its calculation, its relationship with shear stress for both Newtonian and non-Newtonian fluids, and the measurement of shear strain rate using rheometers.
What is Shear Strain Rate
Shear strain rate is a measure of the rate at which a substance deforms under shear stress. In fluid mechanics, it plays an important role in characterizing the flow behavior of fluids, particularly in the study of viscous flows. The concept of shear strain rate is essential in understanding the dynamics of fluid flows and their interaction with solid boundaries, such as in pipe flows and boundary layers.
Shear strain rate can be mathematically defined as the derivative of shear strain with respect to time, such that:
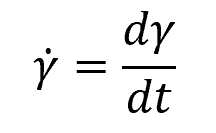
Where:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
- γ̇ = shear strain rate [s-1]
- γ = shear strain [unitless]
- t = time [s]
This is illustrated in the diagram below.
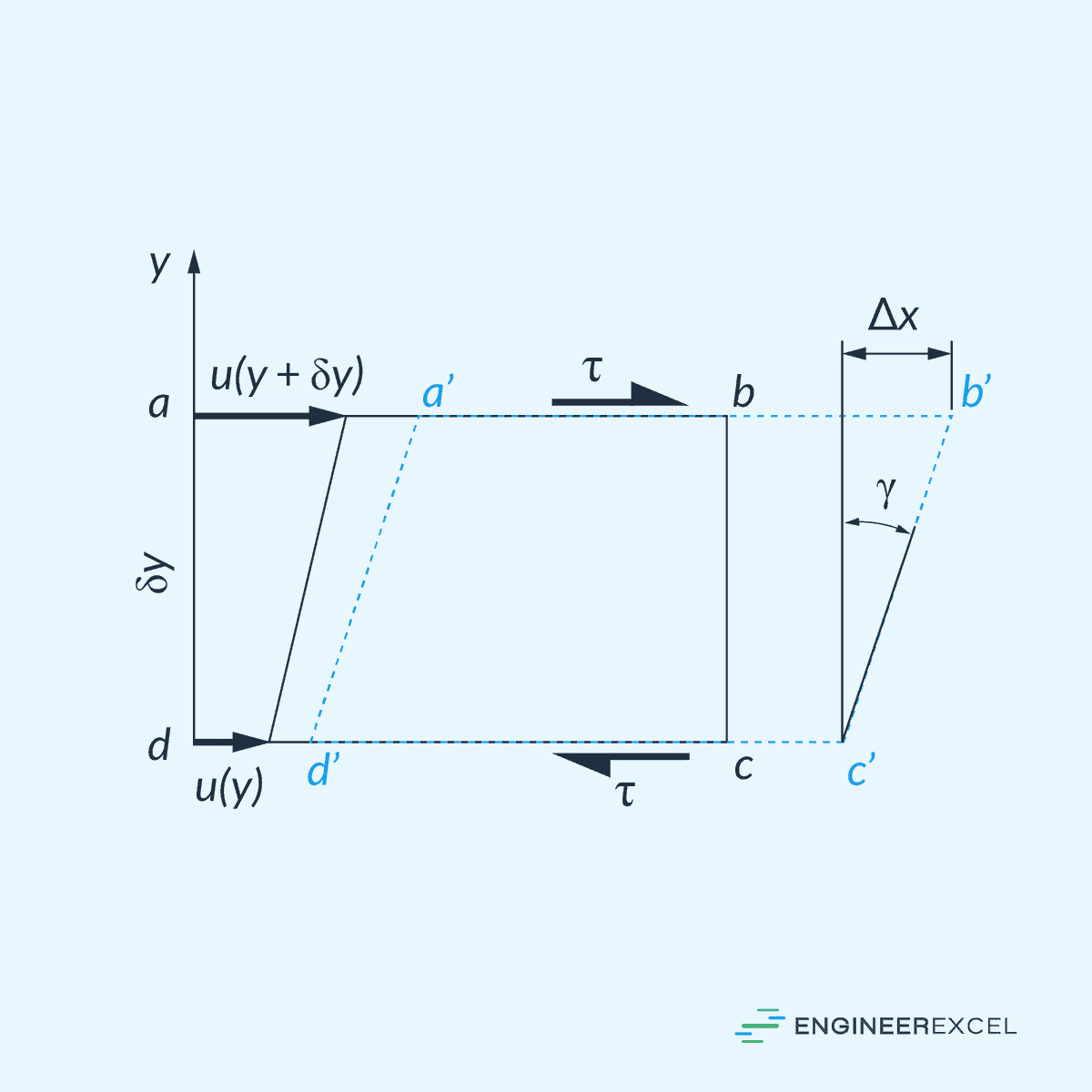
In Cartesian coordinates, it is given by the partial derivative of the velocity components along the principal axes:

Where:
- u = velocity component in the x directions [m/s]
- v = velocity component in the y directions [m/s]
The viscosity of a fluid plays a significant role in determining the shear strain rate. For Newtonian fluids, the viscosity is typically influenced by temperature. As temperature increases, the viscosity of most fluids decreases, leading to higher shear strain rates.
For non-Newtonian fluids, the behavior of the viscosity is more complex. The viscosity of non-Newtonian fluids depends on factors such as temperature, time, and shear stress. Different types of non-Newtonian fluids exhibit varying responses to shear, and their viscosity may change with the applied shear rate or stress.
Shear Stress vs Shear Strain Rate
Shear stress in fluids refers to the force applied parallel to the surface of the fluid, divided by the area over which it is applied. It represents the intensity of the internal forces within the fluid that resist the sliding of adjacent layers. Shear stress causes continuous shear deformation in a fluid.
Shear strain rate, on the other hand, is a measure of the rate at which adjacent fluid layers deform or move relative to each other under the influence of shear stress. It is the change in shear strain (the deformation) per unit of time.
For Newtonian fluids, the relationship between shear stress and shear strain rate comes from the Newton’s law of viscosity. This linear relationship can be expressed as:
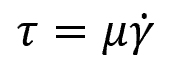
Where:
- τ = shear stress [Pa]
- μ = dynamic viscosity of the fluid [Pa-s]
According to Newton’s law of viscosity, the shear stress is directly proportional to the shear strain rate. So, as the shear strain rate increases, the shear stress also increases proportionally for a Newtonian fluid.
Non-Newtonian fluids, on the other hand, exhibit more complex behavior. The relationship between shear stress and shear strain rate in these fluids is nonlinear, and various rheological models are used to describe this behavior. Some of the commonly used rheological models include:
- Power-law model: Describes the relationship as a power-law function, where the shear stress is a power of the shear strain rate. The power-law model is also known as the Ostwald-de Waele model.
- Bingham plastic model: Assumes that the fluid has a yield stress, below which it behaves like a solid (no flow), and above which it behaves like a Newtonian fluid.
- Herschel-Bulkley model: An extension of the Bingham plastic model that includes a power-law behavior beyond the yield stress.
There are other rheological models as well, and the choice of model depends on the specific characteristics of the non-Newtonian fluid being studied. These models are important in industries such as food processing, pharmaceuticals, and oil and gas, where the flow behavior of materials is a critical factor in the manufacturing and processing processes.
The diagram below shows the behavior of shear stress with respect to shear strain rate of various types of non-Newtonian fluids as well as that of Newtonian fluids.
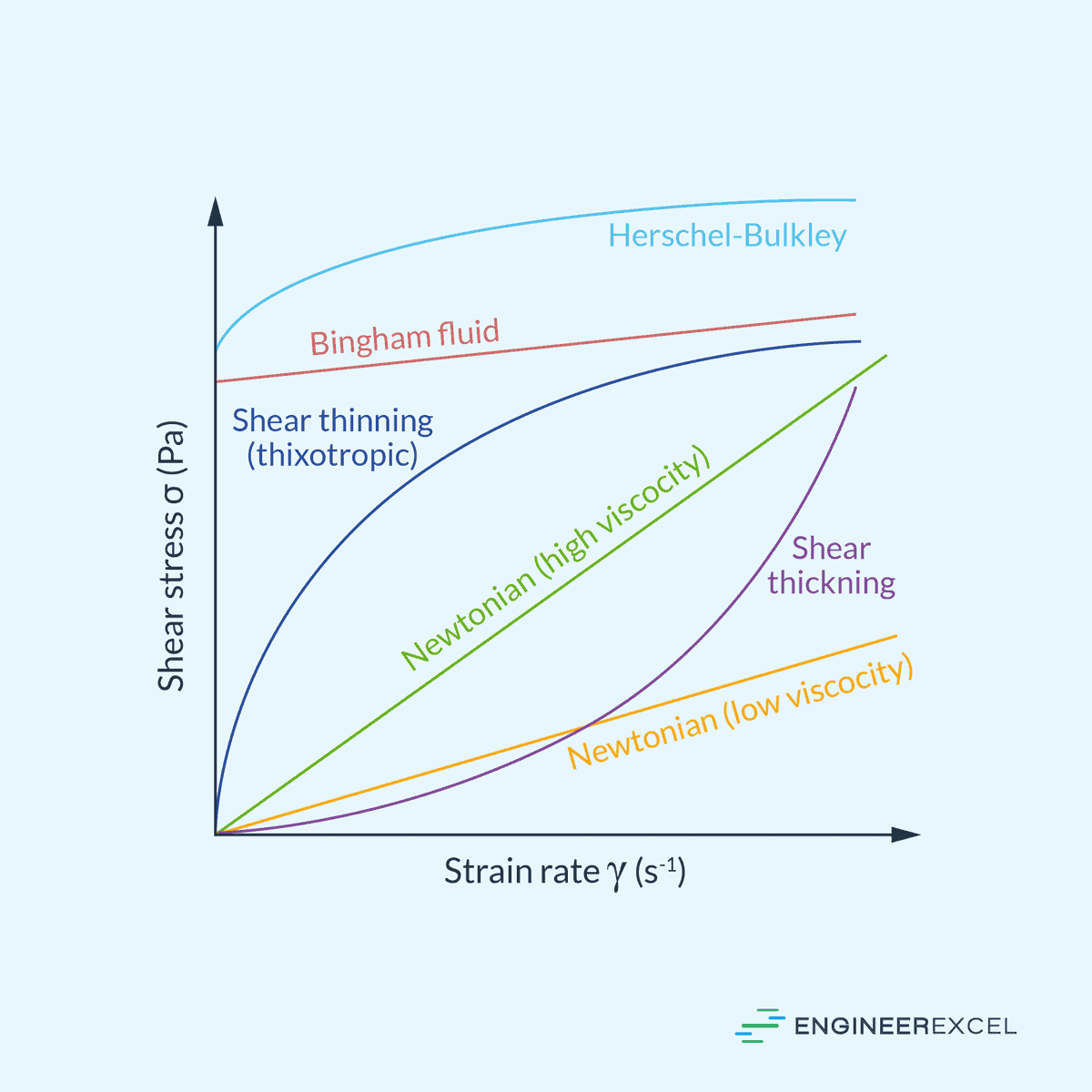
Measuring Shear Strain Rate
Fluid shear strain rate is typically measured using devices called rheometers. These are versatile instruments that can measure not only shear strain rate but also other rheological properties of fluids, including viscosity, shear stress, and viscoelastic behavior. They are often used for complex analyses of fluid behavior, especially in materials that exhibit non-Newtonian behavior where viscosity is not constant under different shear rates.
Rheometers consist of two main components: a stationary part and a movable part. The geometry of these parts can vary based on the type of rheometer and the specific properties being measured. The most common geometries include concentric cylinders, parallel plates, and cone-and-plate configurations.
The fluid or material being tested is loaded onto the rheometer between the stationary and movable components.
The rheometer then applies a controlled deformation to the material. This deformation could be in the form of shear stress, rotational or oscillatory motion, or other controlled modes depending on the rheometer design.

As the material deforms, the rheometer measures the resulting stress and strain in the material. The stress is typically applied by a motorized system, and the resulting deformation is monitored and recorded.
From this data, the shear strain rate can be calculated by taking the derivative of the shear strain with respect to time. The data collected during the rheological measurements are analyzed to characterize the material’s rheological behavior. This includes determining viscosity, elasticity, and other relevant properties.
Different types of rheometers may use different techniques and modes of operation, such as rotational rheometry, oscillatory rheometry, or capillary rheometry. The choice of rheometer and its configuration depends on the specific properties of the material being tested and the conditions of interest.
