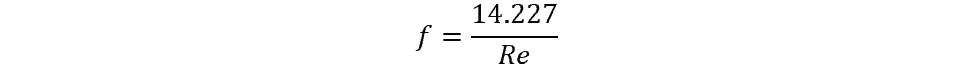In fluids engineering, it is often necessary to calculate the pressure change, or head loss, due to friction. As a fluid flows through a pipe, the interaction of the fluid particles with the wall of the pipe will cause friction, which slows the particles and decreases the pressure. In order to calculate this change in pressure, a friction factor, of which the Fanning friction factor is one example, is used.
While the Fanning friction factor is something that is well understood in modern engineering applications, how to calculate the factor and when to use Fanning friction factor may not be so well understood, depending on the experience of an engineer.
When to Use Fanning Friction Factor
Although any friction factor can be used to determine the head loss due to friction in a pipe, there are certain times when the Fanning friction factor is more often used. Generally, the Fanning friction factor is used by engineers in the field of chemical engineering, or by engineers using British units instead of SI units.
Applying the Fanning Friction Factor
When calculating the head loss, or pressure change, due to friction, the Fanning friction factor is applied as follows:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.

where Δh is the head loss, u is the velocity of the flow, L is the length of the pipe, and g is the gravitational acceleration.
With this equation, an engineer is able to determine how much pressure will be lost as the fluid flows through a pipe. Again, it is important to note which friction factor is being used because factors other than the Fanning friction factor will have a different equation for calculating the head loss.
Calculating the Fanning Friction Factor
Depending on the ultimate application, the Fanning friction factor can be calculated using a number of methods. In some situations, the calculation is as simple as a division problem. However, other situations may require a numerical solver. Regardless of the method, the calculation involves three key components: the Reynolds number and the relative roughness and diameter of the pipe.
The Reynolds number
The Reynolds number is a factor that is used to express how turbulent the flow of a fluid is. The higher the Reynolds number, the more turbulent the flow. Generally, a Reynolds number greater than 3000 is considered to be turbulent flow, while anything less may be considered laminar flow.
The difference between laminar and turbulent flow presents the first situation in which the calculation of the Fanning friction factor can be simplified. If the flow is laminar, the calculation can be reduced to:
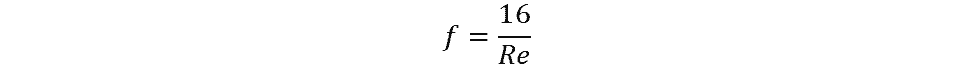
where f is the Fanning friction factor and Re is the Reynolds number. Note, that other friction factors, such as the Darcy friction factor, will be identified with a different symbol (fD in the case of the Darcy friction factor), and it is important to ensure the correct friction factor is being used.
The relative roughness
The relative roughness of a pipe is a measure of how rough the wall of the pipe is compared to a completely smooth surface. The calculation of the relative roughness is the ratio of the average height of the surface irregularities to the total diameter of the pipe, as follows:
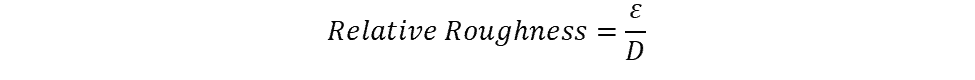
where ε is the average irregularity height, and D is the diameter of the pipe.
Again, if the flow through the pipe is laminar, the relative roughness is not considered in the calculation of the Fanning friction factor. Another time at which the relative roughness is not needed is if the flow is exceedingly turbulent, that is, the flow has a very large Reynolds number.
The pipe diameter
The diameter of the pipe plays a role in not only calculating the relative roughness, but is also a component of the equation for the Fanning friction factor. A pipe with a larger diameter will have a lower Fanning friction factor because more of the flow through the pipe is unaffected by the friction stemming from the interaction of the fluid with the wall of the pipe. In situations where the pipe is not circular, it may be possible to simplify the calculation depending on the shape.
The general equation for the Fanning friction factor
In scenarios where the Fanning friction factor cannot be simplified due to laminar flow or the shape of the pipe, the general form of the Fanning friction factor equation is:

Looking at the general form of the equation, it can be seen that it cannot be solved without iteration or a numerical solver. Through the years, simplifications have been introduced to make it easier to solve the equation based on some valid assumptions. These simplifications apply to different scenarios and use a variety of coefficients to replace factors in the equation.
Using a numerical solver or simply iterating on the formula has become trivial with the development of computers and advanced calculators. Therefore, oftentimes a simplification is no longer necessary. However, there are other methods for determining the Fanning friction factor, which can be just as accurate as performing an iterative calculation.
Other methods to find the Fanning friction factor
One of the easiest ways to find the Fanning friction factor is to use what is called a Moody chart. The Moody chart was originally developed to be used in finding the Darcy friction factor, but the principle has been extended to the Fanning friction factor.
A Moody chart provides an engineer with a set of lines that trace the relationship between the relative roughness of the pipe and the Reynolds number of the flow, with each of the lines representing a Fanning friction factor. Usually, the type of friction factor will be labeled on the chart, but if it is not, it is possible to determine if the Fanning friction factor is shown by looking at the friction factor for a Reynolds number of 1000 at the specified roughness; if the value is 0.016, it is the Fanning friction factor.
As mentioned, the Darcy friction factor is another factor that is common in evaluating friction loss in a flow. If the Darcy friction factor is known, a convenient way to calculate the Fanning friction factor is to simply divide the Darcy friction factor by 4:
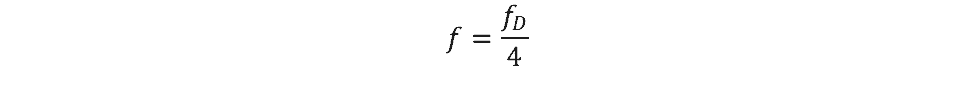
For situations other than a round pipe with turbulent flow, one of the many simplifying equations may be used in determining the Fanning friction factor. For example, in a square channel with laminar flow, the equation is: