Inherently, turbulent flow will always be unsteady. It has random fluctuations in speed, kinetic energy, temperature and more, that make perfectly tracking it an impossible task. However, with that said, turbulent flow may be considered statistically steady in practice, for certain flow situations.
Is Turbulent Flow Steady or Unsteady?
Turbulence in considered to be fundamentally unsteady. In definition, turbulence is transient, it changes over time. And that is the key to turbulence: it is unsteady because it changes over time.
Defining something as a “steady” is generally reserved for laminar flows, fluids maintain consistent properties. Laminar flows may be unsteady as well, but they are the only type of fluid flows that can technically considered to be steady. The difference with laminar flows is that they generally move at slower velocities, lower Reynolds numbers, and move slower relative to their viscosities.
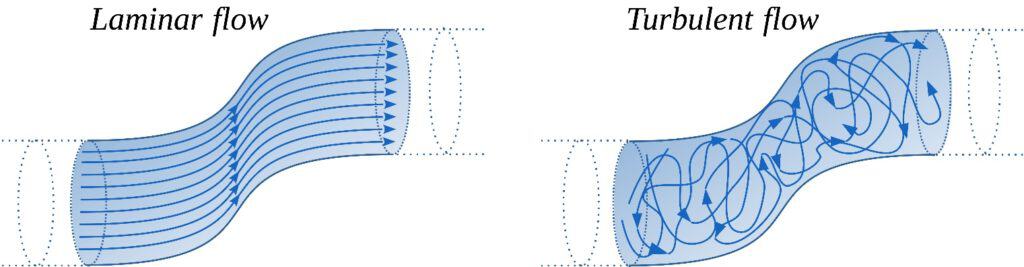
Unsteady derives from how a fluid will change over time (with all “input” conditions remaining the same). An unsteady fluid will generally have a high Reynolds number and be subject to a whole host of changing properties. This can range from the creation of vortices and flow eddies, separating boundary layers, and cross currents, all of which can arise, change, or disappear with the passage of time. Turbulent flows are said to be functions of time.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
With all that said, turbulent flows can be considered steady for experimental purposes in certain situations. A better way of putting it would be to say that certain turbulent flows can be considered ‘statistically stationary’. What this means is that while quantities like velocity, kinetic energy, and streamline direction will fluctuate over time, on average they will not change. Thus, they are statistically steady.
Is Turbulent Flow Stable?
Stability of a flow means that an isothermal (constant temperature) flow subjected to a small disturbance, a one-off event that happens in the flow, will not significantly change due to this disturbance. The flow system will return to its original state after a short period of time. This disturbance would relate to an internal characteristic of the flow itself, be it a change in velocity or pressure or density.
In a flow that is said to be unstable, on the other hand, some disturbance will cause a growing effect within a fluid that irreversibly changes it. While not every disturbance will cause this, if at least one does, the flow is said to be unstable. Often the new flow from this disturbance will also be steady, just with a different flow profile. This is not always the case, however.

Flow stability depends highly on the Reynolds number. There will be a critical Reynolds number value for some disturbance that changes the flow from stable to unstable. This critical Reynolds number will also cause the flow to transition from laminar to turbulent.
By definition, a turbulent flow cannot be stable because it is changing with time, and a flow that has been permanently changed via a disturbance is considered unstable. Flows also are said to transition from laminar to turbulent at a critical Reynolds number value, another way of thinking about the transition from stable to unstable.
It should be noted that not every laminar flow will transition to a turbulent flow with a critical Reynolds number if subjected to a disturbance. Occasionally it will shift to a flow with a different Reynolds number that is still below critical level. In other rare instances, flow can transition to unstable even below the critical Reynolds value – called subcritical instabilities. These cases are not common, but they can happen.
Reynolds Number Explained
There are several variables needed to consider when studying turbulent flows, especially if trying to determine whether a fluid has transitioned from laminar flowing to turbulent. Things like rotational energy, diffusivity (how well something mixes) and dissipation properties, the density and viscosity of a fluid, and the length of flow across an object all have great effects on turbulence. What ultimately determines whether a flow is laminar or turbulent is what is known as its Reynolds Number.
Reynolds Number is defined as:
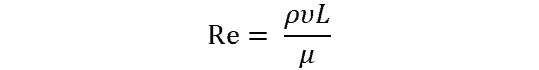
where
- ρ = fluid’s density (kg/m3)
- υ = flow speed (m/s)
- L = length of the linear dimension of flow (m)
- μ = the dynamic viscosity of the fluid (kg/m-s)
The Reynolds number is a dimensionless quality, as shown by the unit cancellations in the equation above. Lower Reynolds numbers indicate laminar flow, while higher define turbulent. The generally accepted scale is that a Reynolds number of less than 2300 means laminar flow, a Reynolds number above 4000 means turbulent, and anything in between is to be defined as transitional flow.
Just knowing whether a flow is turbulent is not enough to properly study it, however. Indeed, Reynolds numbers are often too large in flows of interest for today’s computers to run Direct Numerical Simulations (DNS) on. The computational power to run DNS of flows using the Navier-Stokes equations (widely believed to properly describe much turbulent flow) is still lacking in today’s world. Wild energy fluctuations cascade into more whorls and eddies, and more instability, complicating any study of turbulence. This is an important problem, because the biggest issue turbulent flows cause is resistance, a big drain on efficiency and fuel consumption.
Can Turbulent Flow Be Stationary?
Stationary flow means the same thing as steady-state flow. If a flow is not dependent on time, then it is said to be stationary. In other terms, the velocity of a fluid particle at a specific position (across the entire fluid field) that does not change is considered stationary.
As discussed above, turbulent flows are not steady or stationary, precisely because velocity and pressure change over time. However, if this average particle velocity over time basically does not change, it can be considered stable or stationary for practical purposes.
Turbulent Mixing Defined
Turbulent flows are said to mix more quickly than laminar flows. But what is mixing of a fluid flow?
There are endless examples of distinct fluids mixing in everyday life, from stirring creamer into coffee to diluting cleaning fluids with water. If one wants to mix these fluids together more quickly, adding in “disturbances” (like the rapid stirring of a spoon) that create turbulence would be a way to do so.

There’s a lot that goes on behind the scenes of mixing fluids, and there are several coefficients and equations that define how and why mixing occurs. But without delving too deep into the weeds on turbulent mixing, it’s important to note how turbulence affects it. Turbulent flows, with unstable changes in things like velocity, pressure, and temperature all encourage fluid mixing as they increase.
The Challenges of Turbulent Flow
Because of the random nature and irregularity of turbulent streams, they are notoriously difficult to understand and apply some level of order through equations. Unsteady flows, that change with time, add an even higher degree of difficulty when studying turbulence.
Even attempting to take measurements and interact with turbulent flow creates effects that make analysis difficult. The influential American physicist Richard Feynman described turbulence as “the most important unsolved problem in classical physics”, which is a pretty big problem if turbulent flow is found everywhere from cigarette smoke to cardiology to rocket exhaust!
