The Hagen-Poiseuille equation is a fundamental concept in fluid dynamics, describing the relationship between pressure drop and flow rate in a cylindrical pipe for laminar flow. Developed by Gotthilf Hagen and Jean Léonard Marie Poiseuille in the 19th century, this equation remains widely applicable in engineering and industrial processes. It is essential for understanding fluid behavior, solving real-world problems, and optimizing transport processes.

This article explores the derivation, application, assumptions, limitations, and contributions of the Hagen-Poiseuille equation, providing a comprehensive understanding of its role in modern fluid dynamics.
Hagen-Poiseuille Equation Fundamentals
Pressure Difference
The Hagen-Poiseuille equation deals with the relationship between pressure difference, flow rate, and resistance of a fluid flowing through a pipe. The pressure difference is a significant factor that drives the fluid flow inside a pipe. The higher the difference in pressure between the two ends of the pipe, the greater the flow rate will be.
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
The Hagen-Poiseuille equation, solved for flow is as follows:
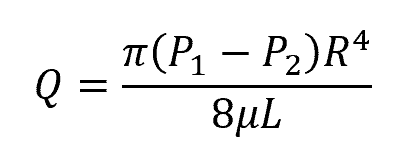
where
- Q is the flow rate
- P1 and P2 are the pressures at the two ends of the pipe
- R is the pipe radius
- µ is the fluid’s viscosity
- L is the pipe length
Laminar Flow
The Hagen-Poiseuille equation applies exclusively to laminar flow, a type of fluid flow characterized by the absence of turbulence. In laminar flow, fluid particles move along smooth, parallel paths with little to no interaction between layers. The velocity profile of laminar flow in a pipe is parabolic, with the fluid moving fastest along the centerline, as shown in the image below.

Incompressible Fluid
The equation assumes that the fluid flowing through the pipe is incompressible. Incompressible fluids maintain a constant density regardless of changes in pressure. This characteristic simplifies the complex relationships between pressure, flow rate, and resistance in the equation. Most liquids, including water, have this property and are considered incompressible fluids.
Newtonian Fluid
Another assumption made by the Hagen-Poiseuille equation is that the fluid is Newtonian. Newtonian fluids have a linear relationship between their viscosity and the applied shear stress, meaning their viscosity remains constant under different shear rates. This constant, predictable behavior allows the equation to accurately model fluid flow through a pipe.
Hagen-Poiseuille Equation vs. Darcy-Weisbach Equation
The Hagen-Poiseuille equation and the Darcy-Weisbach equation are both used to calculate pressure drop due to fluid friction in pipelines. However, they are used in different situations.

The Hagen-Poiseuille equation calculates pressure drop in laminar flow, where the fluid flows smoothly in parallel layers. It assumes the flow is steady and incompressible, and the pipe is straight and circular with a constant diameter. The equation uses the viscosity of the fluid, the pipe diameter, and the flow rate to calculate the pressure drop.
The Darcy-Weisbach equation, on the other hand, is used to calculate pressure drop in turbulent flow, where the fluid flows in a chaotic manner with eddies and swirls. It also assumes that the flow is steady and incompressible and the pipe is straight and circular with a constant diameter. However, the Darcy-Weisbach equation uses the friction factor, which depends on the roughness of the pipe surface and the Reynolds number, along with the fluid density, velocity, and pipe diameter, to calculate the drop in pressure along a pipe length.
Applying the Hagen-Poiseuille Equation
Flow Rate
The Hagen-Poiseuille equation relates the flow rate of a fluid through a cylindrical pipe to the pipe radius, pipe length, and viscosity of the fluid. The flow rate is directly proportional to the fourth power of the pipe’s radius, which means that even a small increase in the pipe’s radius will result in a significant increase in the flow rate.
Pressure Drop
The pressure drop is the difference in pressure between two points along the pipe. Using the Hagen-Poiseuille equation, we can also express pressure drop as:
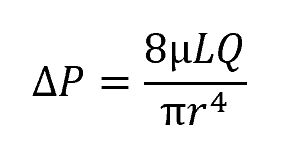
It becomes evident that higher viscosity fluids and longer pipes result in higher pressure drops.
Resistance
Fluid resistance opposes the flow of fluid through a pipe and is primarily influenced by factors like viscosity, length, and radius. From the Hagen-Poiseuille equation, the resistance can be defined as:

In this context, resistance is analogous to electrical resistance in Ohm’s Law, with pressure drop analogous to voltage, and flow rate analogous to current.
Volumetric Flow Rate
The volumetric flow rate (Q) is the rate at which fluid flows through a pipe in terms of volume per unit of time. The Hagen-Poiseuille equation gives a direct relationship between the volumetric flow rate, pressure drop, radius, viscosity, and the length of the pipe.
Advanced Applications and Topics
Reynolds Number
The Reynolds number, a dimensionless quantity, is crucial in determining whether the flow within a tube is turbulent or laminar and, therefore, whether the Hagen-Poiseuille equation applies. It is calculated as follows:
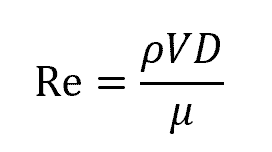
Where
- ρ is the fluid density
- V is the mean fluid velocity
- D is the pipe diameter
- µ is the dynamic viscosity
For a lower Reynolds number (< 2000), the flow is considered laminar, and the Hagen-Poiseuille equation is applicable.
Shear Rate
Shear rate is crucial in understanding the parabolic profile of fluid velocity distribution within a tube. It is the derivative of velocity with respect to radial distance (r) from the centerline of a capillary tube:
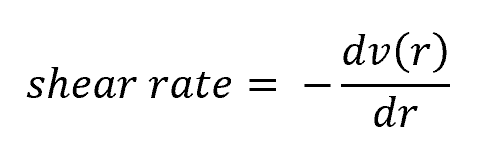
Where v(r) is the radial velocity profile. The Hagen-Poiseuille law establishes a relationship between shear rate, fluid viscosity, and pressure loss along the tube length that results in a parabolic velocity distribution.
Rheology
Rheology encompasses the study and characterization of fluid flow behavior, particularly for non-Newtonian fluids, where viscosity is not constant but rather, depends on factors like shear rate, temperature, and concentration. In microfluidics, the Hagen-Poiseuille equation serves as a basis for understanding how fluid viscosity affects the volume flow rate and pressure drop across the capillary tube.
Challenges and Limitations
No-Slip Condition
The no-slip condition is a key assumption in the Hagen-Poiseuille equation that states the fluid is in contact with the apparatus wall, creating a stationary layer. However, this condition may not always hold true in real-life scenarios. The presence of irregular surfaces, high shear rates, or unique rheological properties can potentially invalidate the no-slip assumption.
Constriction and Obstruction
Constrictions and obstructions can significantly affect the flow of fluid in a system. The Hagen-Poiseuille equation assumes a uniform cylindrical pipe, but in many cases, tubes or conduits may have non-uniform diameters or contain obstructions. This can lead to inaccurate predictions of flow rate and resistance. For example:
- In biological systems, valves control blood flow and can impact the predicted flow rate.
- Air often flows through ducts of rectangular cross section. The Hagen-Poiseuille equation cannot be used in these instances.
- Porosity and shape factor play a significant role in determining flow behavior in porous media, which can affect flow rate calculations.
