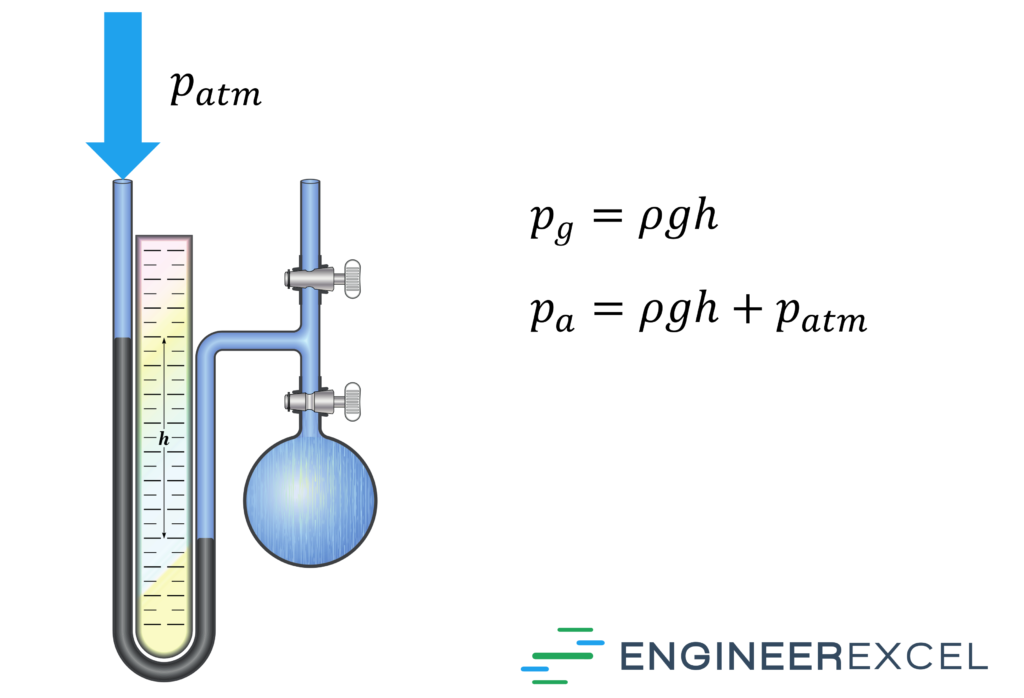
A manometer is a measuring instrument used to indicate the pressure of a fluid or gas. It indicates the pressure relative to the atmospheric pressure, in the case of an open manometer, or full vacuum, in the case of a closed manometer.
Manometers come in analog and digital form. The simplest and most well-known manometer is the U-Type, which consists of a glass tube shaped like a U with numbers listed and spaced on each side. A liquid is poured into the instrument until it sits between the legs of the U. When pressure is applied, the liquid moves, and the height is measured. If water is the liquid in the manometer, the height is expressed in inches of water column (inWC). If mercury is the liquid in the manometer, the pressure is expressed in inches of mercury (inHg) or millimeters of mercury (mmHg)
Different manometer equations are used to calculate the pressures of fluids and gases under various circumstances from manometer readings. Open, closed, inclined, and inverted equations are the most used.
Open Manometer Equation
This equation is commonly used to measure gauge pressures. The formula is
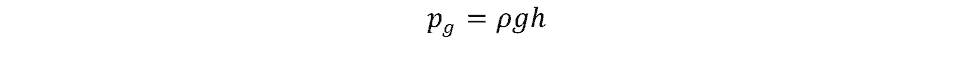

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
where:
- pg = gauge pressure relative to the atmosphere
- ρ = density of liquid in the manometer
- g = gravitational acceleration of 9.806 m/s² (or approximately 32.174 ft/s²)
- h = height difference between the legs of the manometer
An open manometer can also be used to measure absolute pressure. In this case, the formula is:
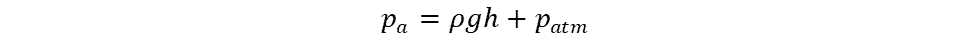
where:
- pa = absolute pressure
- patm = the atmospheric pressure.
Closed Manometer Equation
In a
The
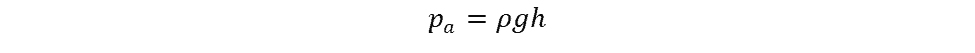
where:
- pa = absolute pressure
- ρ = density of the manometer liquid
- g = acceleration due to gravity
- h = height difference between the legs of the manometer
Inverted Manometer Equation
An inverted manometer is used to measure pressure differences in liquids. Air or another gas fills the space above the liquid in the device and can be bled or expelled through the top to adjust its level. The equation is:
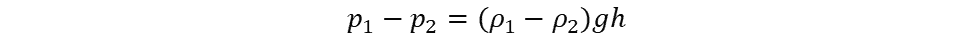
where:
- p1 = pressure in liquid 1
- p2 = pressure in liquid 2
- ρ1 = density of liquid 1
- ρ2 = density of liquid 2
Inclined Manometer Equation
Inclined manometers are useful for situations where the pressure to be measured is small. That’s because the incline of the tube allows for large spacing between the gradations in the cylinder.
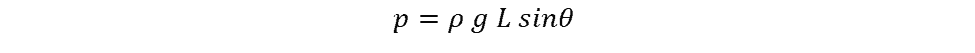
where:
- p = gauge pressure if the manometer tube is open, or absolute pressure if closed
- ρ = density of the manometer fluid
- L = length of the tube that is filled with manometer fluid above the baseline
- θ = angle of the manometer tube from horizontal
Manometer Flow Rate Equation
A manometer can be used to determine the flow rate across an orifice by measuring a pressure difference. One leg of the manometer is connected to the pipe upstream of the orifice and the other leg of the manometer is connected downstream of the orifice. The pressure differential across the orifice can be used to calculate the flow rate using the orifice equation:
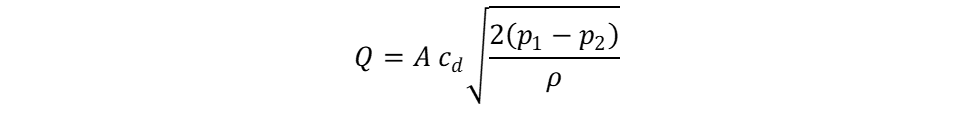
Substituting the manometer equation yields the following:
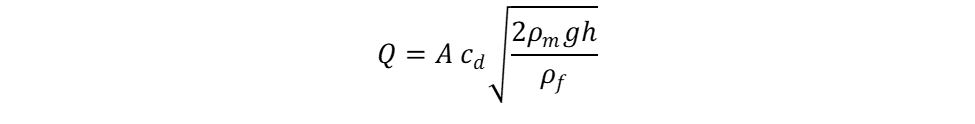
where:
- Q = volumetric flow rate of the fluid in the pipe
- A = cross sectional area of the orifice
- cd = discharge coefficient of the orifice
- ρm = density of the manometer liquid
- g = gravitational acceleration
- h = height difference in the manometer
- ρf = density of the fluid in the pipe
Manometer Equation Example
Question
A pressure is applied to one end of an
Solution
The density of mercury, ρ, is 13,500 kg/m3.
Calculate the pressure using the
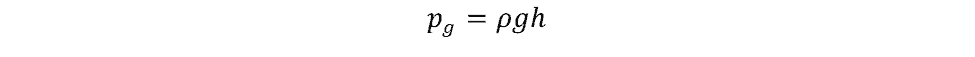
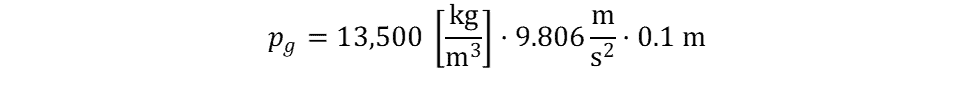
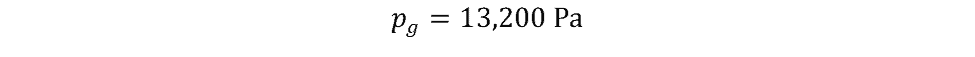
The applied pressure is 13,200 Pascals (gauge) or 1.92 psig.
Can a Manometer Measure Vacuum Pressure?
Vacuum is a pressure that is less than atmospheric pressure. When measuring vacuum with an
The result of a negative h value is that the pressure calculated from the manometer equation will also be negative. Keep in mind that this represents a pressure that is less than atmospheric. To convert this into a positive absolute pressure, just add the atmospheric pressure to it.
Measuring Vapor Pressure with a Manometer
This is the procedure for measuring the saturated vapor pressure of a pure liquid at a given temperature:
1. Measure the density of the liquid.
2. Fill the manometer with an oil.
3. Fill half round the bottomed flask with the distilled water that will be used to measure the vapor pressure. You must then put a stopper in the mouth of the flask.
4. Verify that the temperature of the water is the same as the ambient temperature of the air.
5. Wait. Allow the equipment to reach a state of equilibrium.
If the meniscuses of oil columns don’t change any more, measure the difference of heights of two oil columns.
How to Choose a Manometer
The type of manometer you choose depends on the type of fluid you want to measure. They are not all suitable for the same kinds of fluids and gases. If you want to measure the pressure of an exceptionally corrosive substance, then you should use a manometer that is made of rustproof steel.
Liquid and digital manometers are also available.
Liquid Manometer
This type of manometer measures differential pressure by balancing the weight of a liquid between two pressures. It uses indicating fluids such as colored water, oil, benzenes, bromides, and mercury. Water can measure small pressure differences, and mercury large pressure differences. The most important things to verify if you decide on a liquid manometer are the specific gravity, operating temperature range, vapor pressure, and flash point of the indicating liquid.
Digital Manometer
A liquid manometer is limited, and is not always suitable for work in the field. It can also be cumbersome to use such a kit if most of the rest of your work is done on a computer. All such challenges can be overcome with a
These microprocessor-based instruments are made as portable units or stand-alone mounting styles. It is easier to come to an accurate result with a digital manometer. You will not have to make the same kinds of manual compensations and corrections that are necessary with liquid manometers. These are all done automatically through software.
Advantages and Disadvantages of a U-Type Manometer
The manometer is an ideal instrument to measure dynamic and differential pressure. Although digital manometers are becoming more and more popular, the U-type device is still in service. Above, we listed some of the advantages of the
Advantages of U-Type Manometer
- Low cost
- Suitable for low-pressure applications
- Simple construction
- Highly sensitive
- No need for calibration against a standard
- Available for a large range of filling fluids at various specific gravities
Disadvantages of U-Type Manometer
- Large and bulky
- Must be levelled
- Possible introduction of error owing to condensation
- No over-range protection
- Poor dynamic response
- Fragile and less portable
- Fluid density dependent on temperature, which can lead to errors
- Slow response, which makes it unfit for measuring fluctuating pressures
Micromanometers
Micromanometers have also become quite popular. They are designed to measure pressure differences that are very small. These are the most sensitive manometers in production, and they are most appropriate for any project that requires accurate and precise readings of the smallest differences.
Micromanometers can be used to measure differential pressures, to calculate velocity or volumetric flow rate, and to test or bring into balance fluid systems.
