The Darcy-Weisbach equation is used to calculate the major pressure loss or head loss in a pipe, duct, or tube as a function of the pipe’s length and diameter, the fluid’s density and mean velocity, and an empirical value called the Darcy friction factor. The equation is valid for both laminar flow and turbulent flow.
What is the formula for the Darcy Weisbach Equation?
Pressure Loss Form
To calculate the pressure loss in pipe flow problems, use the pressure loss form of the Darcy-Weisbach equation:
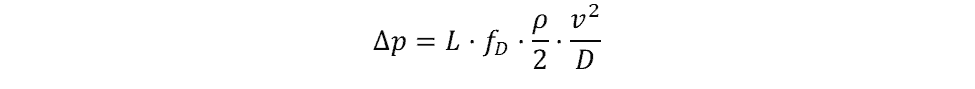
where:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
- Δp = pressure loss [Pa]
- L = the length of the pipe [m]
- fD = Darcy friction factor [unitless]
- ρ = fluid density [kg/m3]
- v = mean fluid velocity [m/s]
- D = pipe diameter (or hydraulic diameter for non-circular ducts) [m]
Sometimes it may be more convenient to express the pressure loss per length of pipe. In that case, both sides of the equation can be divided by L to obtain the following form of the equation:
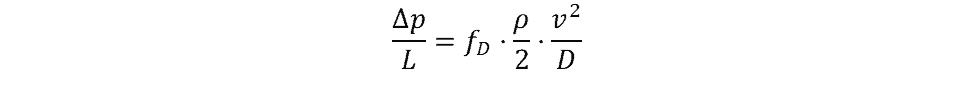
where Δp/L is the pressure loss per unit length.
Head Loss Form
Major losses in piping can also be calculated as head loss by recalling that the pressure beneath a column of a fluid is:
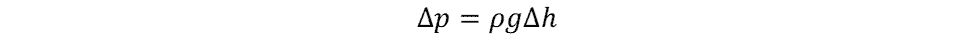
where:
- g = the acceleration due to gravity [m/s^2]
- Δh = the head loss or height of the fluid column [m]
By substituting this definition into the pressure loss form of the Darcy-Weisbach equation, the head loss due to friction in a pipe can be expressed by the following equation:
Darcy-Weisbach Friction Factor
The Darcy-Weisbach friction factor, also known as the Darcy friction factor or just friction factor, is an empirical coefficient required to calculate the pressure drop due to friction loss via the Darcy-Weisbach equation.
The friction factor is a function of Reynold’s number for the flow and pipe characteristics such as roughness height, ε, and diameter, D.
There are several alternative methods for determining the Darcy friction factor.
The Colebrook Equation (or Colebrook White Equation) is the most accurate method for calculating the friction factor. It was developed by fitting a function to experimental data.
The Colebrook equation can be difficult to work with because it cannot be solved directly for the friction factor, f. However, there are Colebrook equation calculators available online as well as methods that can be used to solve the equation using spreadsheets.
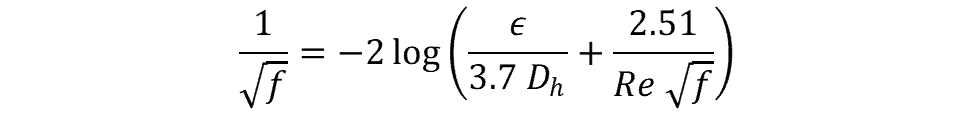
A Moody diagram contains multiple curves of constant relative roughness (ε/D) plotted over a range of Reynold’s numbers.
To find the friction factor on a Moody diagram, calculate the relative roughness and Reynolds number. Find the position on the chart where the relative roughness curve intersects the Reynolds number and find the friction factor corresponding to that point on the left side of the chart.
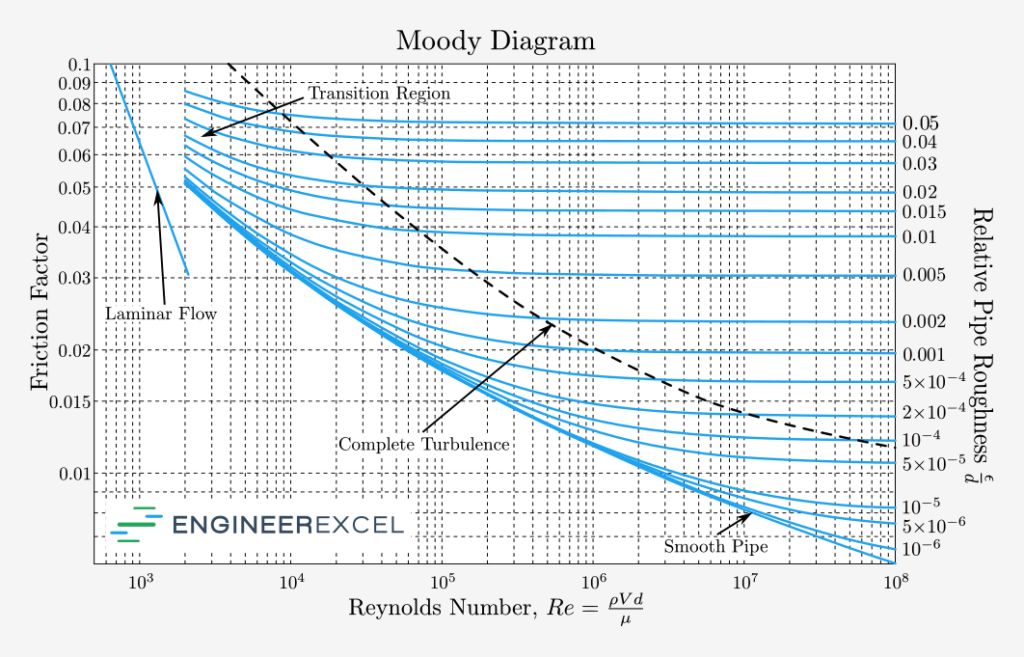
Finally, other equations have been proposed more recently to approximate the Darcy friction factor, that are easier to solve than the Colebrook equation only a minor reduction in accuracy. The Swamee-Jain equation and Haaland equation are two examples.
Darcy-Weisbach Equation Example
Consider the example problem below:
Problem
Room temperature water is flowing at steady state in a cast iron pipe with a diameter of 50 mm at a rate of 0.002 cubic meters per second. What is the pressure loss per meter of pipe?
Solution
Rearrange the equation to calculate the pressure drop per unit length:
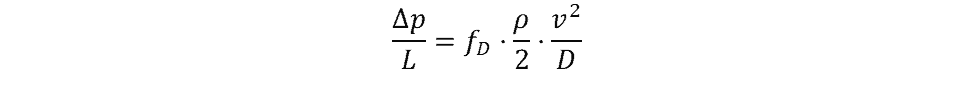
Calculate the cross-sectional area of the pipe:
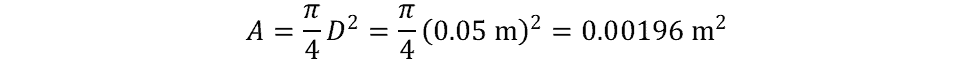
The average fluid velocity is:
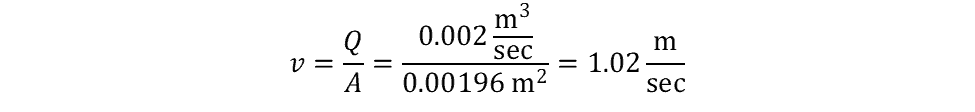
To find the friction factor, two things are necessary: the relative roughness of the pipe and the Reynolds number of the fluid flow.
Relative roughness is defined as the roughness height, ε, divided by the diameter D. For cast iron pipe, a typical roughness value is 0.26 mm, so the relative roughness is:
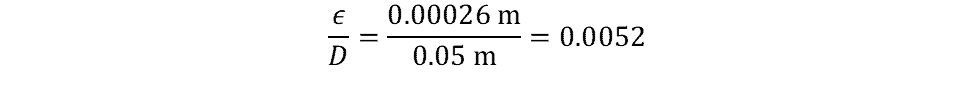
Reynold’s number is calculated from the following equation:
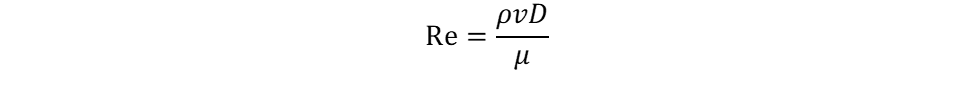
where µ is the dynamic viscosity of the fluid.
The dynamic viscosity of room temperature water is 0.0009737 Pa-s, so the Reynolds number for this flow is calculated as:
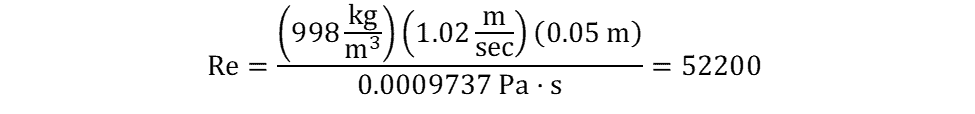
Using one of the methods described above, the unitless friction factor is approximately:
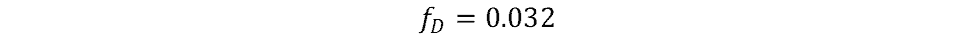
Finally, we can calculate the pressure loss per unit length of the pipe using the Darcy-Weisbach equation:
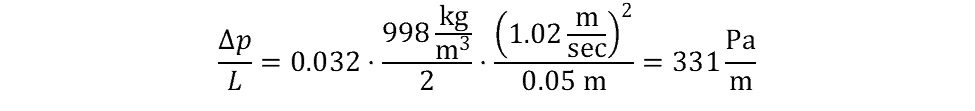
The pressure loss per length of pipe is 331 Pascals per meter.
Darcy-Weisbach Equivalent Length
When the pressure vs. flow characteristics of valves and fittings are expressed as an equivalent length of pipe, the Darcy-Weisbach equation can be used to determine the minor pressure or head loss through those components by substituting the valve or fitting equivalent length for the pipe length term in the equation.
To calculate the pressure loss due to a fitting with a given equivalent length, use the following equation:
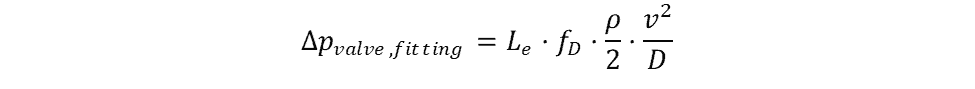
where Le is the equivalent length of the valve or fitting.
To calculate the head loss due to a fitting with a known equivalent length, use this equation:
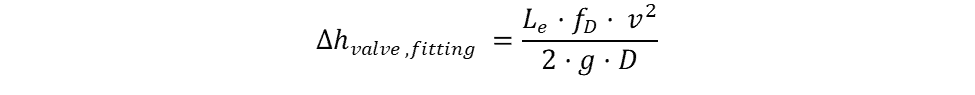
Darcy-Weisbach Equation in US Units
The Darcy-Weisbach equation can be used to solve for pressure drop or head loss in US customary units as well as metric units. To make the units work out, multiply the equation by the fraction gravity divided by the gravitational constant, which equals 1.
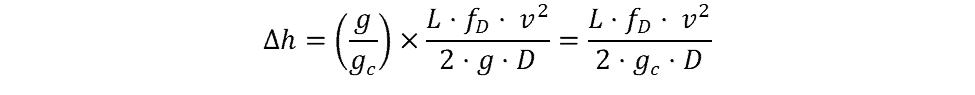
where
- g = acceleration due to gravity [ft/sec2]
- gc = gravitational constant [lbm-ft/lbf-sec2]
- L = the length of the pipe [ft]
fD = Darcy friction factor [unitless]
- ρ = fluid density [lbm/ft3]
- v = mean fluid velocity [ft/s]
- D = pipe diameter (or hydraulic diameter for non-circular ducts) [ft]
Darcy-Weisbach Equation vs. Hazen Williams
One common challenge encountered with the Darcy-Weisbach equation is that, to calculate the friction factor, the Reynolds number must be known. To calculate the Reynolds number, the pipe diameter must be known. This makes the equation difficult to use for pipe sizing calculations because it requires multiple iterations.
When sizing pipes for turbulent flow applications, it’s more efficient to use the empirical Hazen-Williams equation, which does not require prior knowledge of the pipe diameter to solve for the pressure loss.
It’s also important to note that the Hazen-Williams equation only applies to viscosities near that of room temperature water (approximately 1.1 x10-6 m2/s).
In US units, the unit-specific Hazen-Williams equation is:
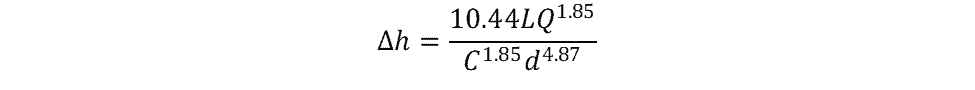
where
- L = pipe length [ft]
- Q = volumetric flow rate [gallons per minute]
- C = roughness coefficient [unitless]
- d = pipe diameter [inches]
The roughness coefficient is tabulated for many different types of pipe. For new, very smooth pipe, the value may be as high as 140-150. For pipes that have been in service for many decades, the coefficient may be as low as 60.
Darcy Weisbach Equation vs. Hagen Poiseuille
When flow is laminar, or has a Reynolds number less than 2000, the Hagen-Poiseuille equation can be used to calculate pressure loss:
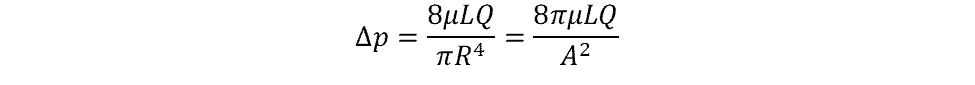
The Hagen-Poiseuille equation can be derived from the Darcy-Weisbach equation by making two substitutions:
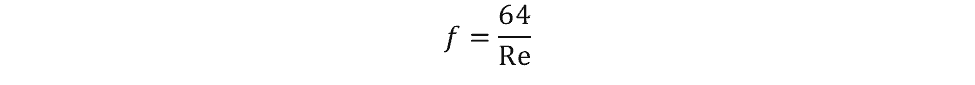
Darcy-Weisbach Equation for Open Channel Flow
The Darcy-Weisbach equation is not useful for open channel flows because it is primarily used for determining pumping requirements for pipes, ducts, and tubes.


