Steady state flow is the condition where fluid properties at any given point within the system don’t change as time passes. These properties include velocity, pressure, and temperature.
One of the most considerable constant properties within the steady state flow system is the mass flow rate, which refers to a lack of accumulation of mass or energy within any part of the system.
For example, steady state flow occurs in a bathtub when the drain is open, but water is concurrently being added. Therefore, if water is exiting the tub at the same rate that water is being entered, the volume will be consistent over time.
What is the Steady State Flow Equation?
In fluid dynamics, the steady state flow energy equation is the mathematical equation that states to ensure a steady flow of the mass flow rate into the control volume is equal to the mass flow rate exiting the control volume. The mass flow rate vector is expressed as a product of density, so the volume flow rate vector (V) and vector area (A) are perpendicular to the flow. The equation results in the product of these integrals over the control surface and is mathematically written as:
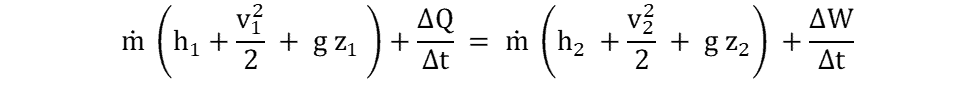
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
where:
- mdot = mass flow rate (kg/sec)
- h = enthalpy (J/kg)
- v = velocity (m/sec)
- g = acceleration due to gravity (m/sec2)
- z = height (m)
- Q = heat (W)
- W = work (W)
What Assumptions Exist for Steady State Flow
There are several assumptions when working with steady state flow. First, the mass flow throughout the systems is constant. Second, the fluid maintains a consistent composition. Third, the only interaction between the surroundings and the system is heat and work. Fourth, the fluid state at any given point is consistent with time. Fifth, flow, kinetic, and potential energies are considered.
What is Steady State Equilibrium?
The state of chemical equilibrium is achieved when the product and concentration of reactants are consistent over time. On the other hand, a steady state occurs when the state variables remain consistent over time while liquid flows throughout the system. The state factor parameters are dependent on the current system state and not the way the system entered that state.
Thermal equilibrium is reached when two contacting objects reach the same temperature, so they aren’t exchanging heat. For instance, if a milk gallon is removed from the refrigerator and placed on the counter at room temperature when the milk and counter reach the same temperature, they have acquired thermal equilibrium.
Why is Steady State Flow Necessary Before Observations?
It is required to wait for steady state flow in any thermodynamic system before taking measurements or making observations because you don’t need to perform heat balance. If the temperatures of cold and hot fluid are steady, then a steady state is indicated by the constant exit temperatures. When making observations, if you’re recording the temperatures and can see the temperature history then the fluid is maintaining consistency, so your observations won’t be skewed by a temperature factor.
This also indicates if there are serious disturbances that could cause the temperature to wildly fluctuate. At this point, it is critical to eliminate those disturbances to acquire accurate measurements or observations.
How Can Steady State Flow be Modeled?
Flow problems found in confined aquifers can be modeled to approximate a real system in three ways:
- The aquifer transmissivity T is constant and homogeneous.
- The flow is steady state.
- The vertical flow resistance is neglected, so only the horizontal flow is accounted for.
By modeling a steady state, you can acquire the results faster and more directly, and in several orders of magnitude, which simplifies post-processing the results. To do so, it’s critical to explicitly define the problem, as steady and solving the system. As the Pareto principle states, you achieve 80 percent of the objective with 20 percent of the effort. Through modeling, you can extrapolate information to gain time on a design exploration where you may run thousands of data points.
What is Pseudo Steady State Flow?
Pseudo steady state flow can be defined as a situation where the pressure at any reservoir point declines at a consistent rate over time. This condition overcomes others as the pressure funnel propagates to every no-flow boundary in the system. A no-flow boundary can be boundaries of drainage areas, the pinch-out of a pay section, or a sealing fault.
What is Steady State Laminar Flow
Laminar flow indicates that the flow of a liquid is smooth with multiple layers, known as lamina, whereby the fluid smoothly moves past each other without convective mixing. Therefore, steady state laminar flow is the maintenance of laminar flow through consistent properties, without outside variables impacting it.
Steady State Flow Applications
There are many forms of steady state in economics, electronics, electrical and mechanical engineering, physiology, fiber optics, and pharmacy, all of which means some type of equilibrium has been achieved. Steady state flow is specific to chemical engineering topics like thermodynamics and chemistry where all variables are consistent, regardless of ongoing processes.
Steady state flow is used in countless products and modern conveniences ranging from the flow of water in a pipe to oil pumping out of a vertical well, turbines on an airplane, and all types of hydraulic systems.
