The Manning equation is an empirical formula used to calculate the velocity of open channel flow, such as in rivers and streams. It relates the flow velocity, channel slope, and roughness coefficient to determine the discharge of water in a given channel.
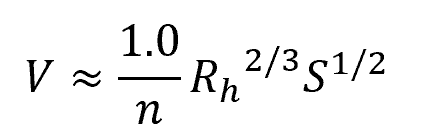
In this article, we will discuss the Manning equation, including its relation to the Chezy equation, the Manning roughness coefficient, and its applications in engineering.
Understanding the Manning Equation
The Manning equation is a widely used empirical formula for calculating the velocity and flow of open channel systems, such as rivers, stormwater drains, and irrigation canals. It is a useful formula especially at locations where it is impractical to construct a weir or flume to measure flow with greater accuracy.
Named after Irish engineer Philippe Manning, who developed the final form of the equation in 1889, the equation is widely used to determine the flow characteristics of open channels and help engineers in designing efficient water management systems, flood protection, and hydraulic control structures. The basic formula of the Manning equation is:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
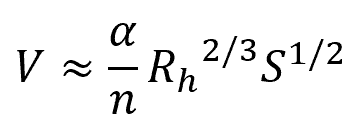
Where:
- V = flow velocity [m/s or ft/s]
- Rh = hydraulic radius [m or ft]
- S = slope of the channel [unitless]
- n = Manning’s roughness coefficient [unitless]
The variable α is a conversion parameter that is equal to 1.0 for SI units and 1.486 for English units.
To get the flow rate, we can simply multiply the above equation by the cross-sectional area of the flow so that it becomes:
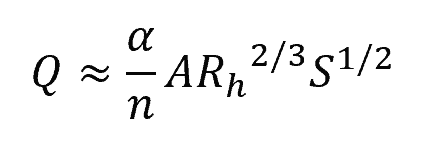
Where:
- Q = flow rate [m3/s or ft3/s]
- A = cross-sectional area of the flow [m2 or ft2]
Derivation from the Chezy Equation
The Manning equation is based on the Chezy equation, which calculates flow velocity using the formula:
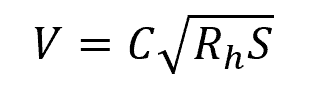
Where:
- C = Chézy coefficient [m1/2/s or ft1/2/s]
Introduced in 1768 by French engineer Antoine de Chézy, the Chezy equation was further developed by Manning to provide a more accurate representation of the connection between hydraulic radius and flow velocity. In tests with real channels, Manning found that the Chézy coefficient C increased approximately as the sixth root of the channel size, resulting in the following formula:
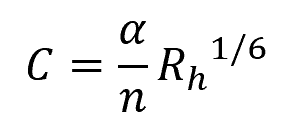
Where:
- n = Manning roughness coefficient [unitless]
Manning introduced the Manning roughness coefficient as a new parameter, which allowed for the creation of a standardized table of values to estimate flow velocity, unlike the Chézy coefficient, which required field measurements for determination.
Manning Roughness Coefficient
The Manning Roughness Coefficient (n) represents the roughness of the channel’s surface, which impacts the flow resistance and, consequently, the velocity of the fluid flow. Its value varies depending on the type and condition of the channel surface.
For instance, for smooth surfaces like concrete, the roughness coefficients tend to be on the lower end, while natural channels with vegetation and irregularities present higher coefficients. Materials such as asphalt or plastic also exhibit specific roughness coefficients, as their texture directly influences flow resistance.
The following table shows some representative Manning’s n values for various channel types and surfaces:
Care should be taken when selecting the appropriate roughness coefficients as incorrect values may lead to significant errors in flow velocity calculations. Comprehensive tables and guidelines for choosing Manning’s n values can be found in various engineering references, which cover a wide range of channel types, materials, and conditions.
Applicability Conditions
The Manning equation is applicable to a variety of flow scenarios in open channel systems. However, there are certain conditions that must be met for the equation to yield accurate results:
- The flow must be steady and uniform, meaning that the velocity and flow rate do not vary over time or along the channel.
- The channel bed slope should be consistent throughout the reach being analyzed.
- The flow should be fully developed, i.e., not affected by upstream or downstream flow obstructions.
- The hydraulic radius and Manning’s roughness coefficient should be representative of the channel geometry and surface roughness.
It is essential for engineers to understand the limitations of the Manning equation and use it within the appropriate conditions to ensure accurate and reliable flow calculations in open channel systems.
Practical Applications of the Manning Equation
The Manning equation is extensively applied in various engineering fields, including hydrology, civil engineering, and environmental engineering.
Stormwater Management
One of the most common applications of the Manning equation is for stormwater management, including sewer system design, sizing detention ponds, and estimating runoff discharge. Engineers use the equation to accurately predict flow capacity, ensuring that the infrastructure is adequately designed to handle stormwater runoff and minimize the risk of flooding.
Irrigation Systems
Efficient water conveyance is vital for agricultural irrigation systems. The Manning equation can be used to design open channels and pipelines, optimizing water distribution to various agricultural fields. This ensures that crops receive adequate amounts of water while minimizing water loss due to excessive velocity, channel roughness, and hydraulic inefficiency.
River Engineering
River engineering involves management and manipulation of river systems to achieve various objectives such as flood control, sediment management, habitat preservation, and navigation. The Manning equation is important in understanding river hydraulics and is used to estimate river discharge under different circumstances. This assists in the design of appropriate river interventions, such as bank stabilization, channel widening, or sediment dredging.
Example Problem
Problem: A rectangular channel has a width (w) of 3 meters and a slope of 0.001. If the channel has a Manning’s roughness coefficient of 0.025, calculate the flow rate through the channel when the water depth (y) is 1.5 meters.
Solution: First, calculate the cross-sectional area:
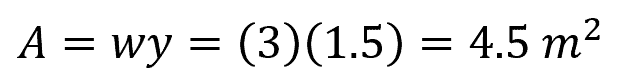
Next, calculate the hydraulic radius, which is equal to the area divided by the wetted perimeter:
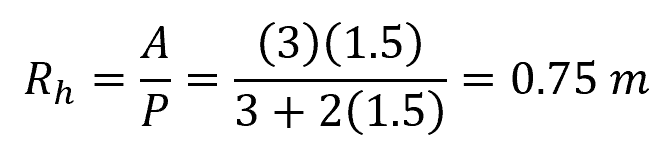
Now we can use the Manning equation to calculate for the flow rate:

Therefore, the flow rate through the channel is 4.7 cubic meters per second.
