Hydraulic radius is a fundamental parameter used in fluid mechanics to characterize the efficiency of an open channel or pipe in conveying fluid. It is calculated by dividing the cross-sectional flow area by the wetted perimeter.
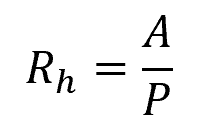
In this article, we will explore the calculation and applications of hydraulic radius in fluid dynamics, including its calculation for different channel shapes as well as its relation to hydraulic diameter.
Hydraulic Radius Definition
Hydraulic radius (RH) is an essential parameter in fluid mechanics and hydraulics that represents the geometric efficiency of a channel or pipe in conveying a fluid. It is generally defined as the ratio of the cross-sectional area (A) of flow to the wetted perimeter (P) of the channel or pipe.
The formula for calculating the hydraulic radius is given by:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
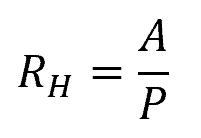
Where:
- RH = hydraulic radius [m]
- A = area of flow [m2]
- P = wetted perimeter [m]
The hydraulic radius plays a significant role in determining the behavior of fluid flow. In open channels and pipes, it influences the efficiency of flow by providing a measure of the space available for the fluid to pass through. A larger hydraulic radius generally indicates a more efficient flow with lower frictional losses, making it a key factor in designing and analyzing hydraulic systems.
Hydraulic Radius of Different Shapes
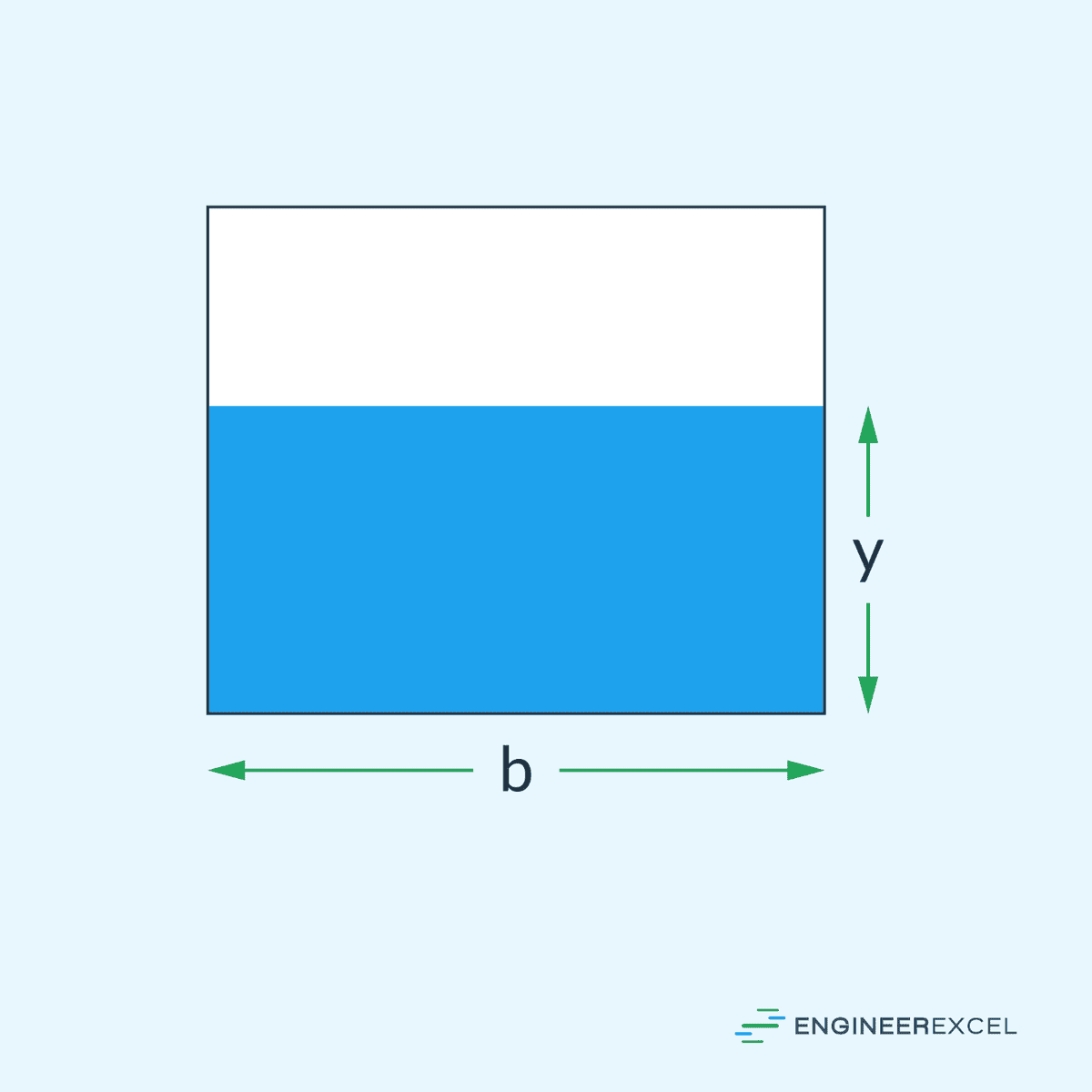
Hydraulic Radius of a Rectangular Channel
For a rectangular channel, the hydraulic radius can be calculated using the formula:
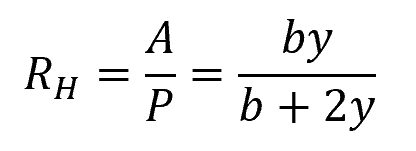
Where:
- b = width of the channel [m]
- y = depth of flow [m]
Hydraulic Radius of a Trapezoidal Channel
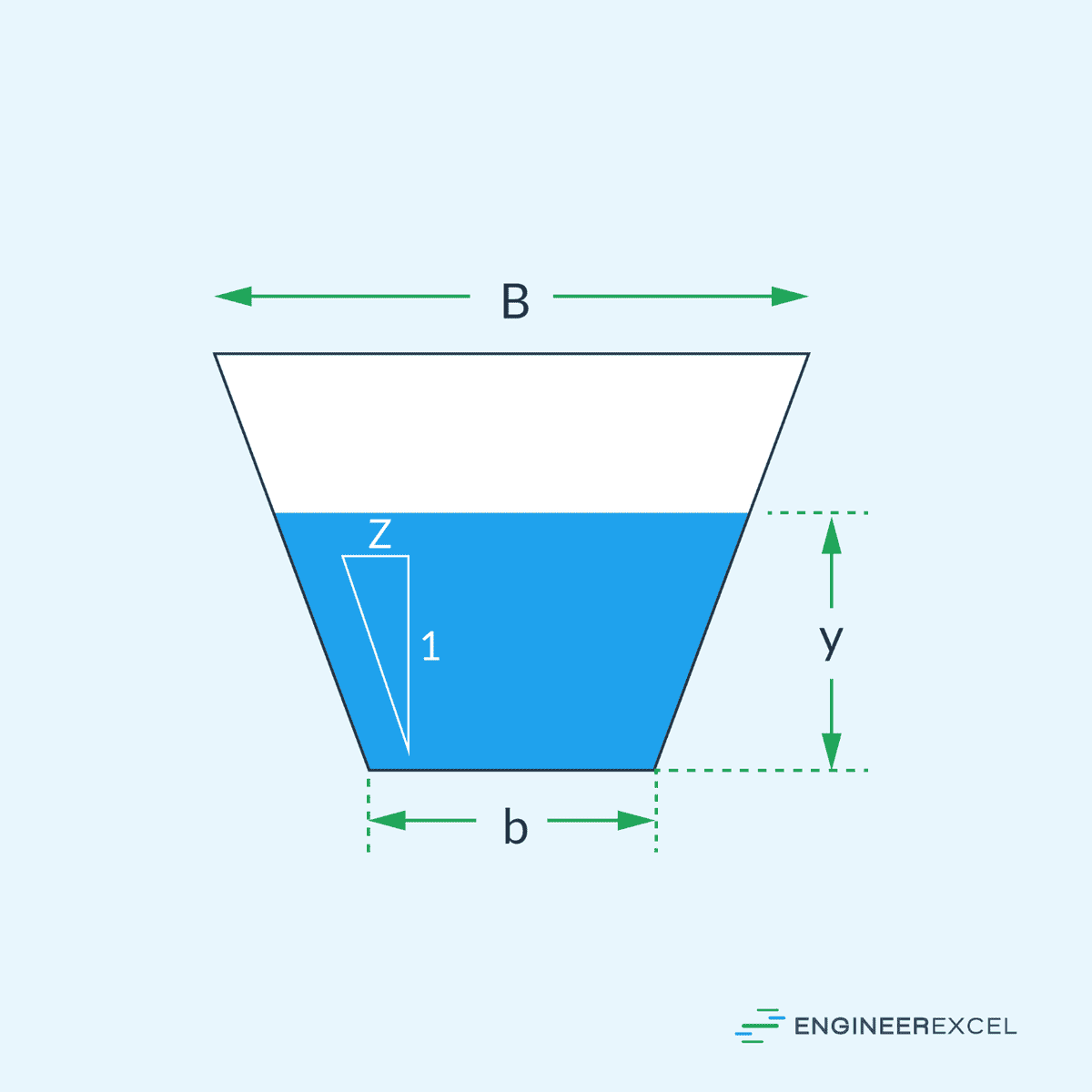
For a trapezoidal channel, the hydraulic radius can be calculated using the following formula:
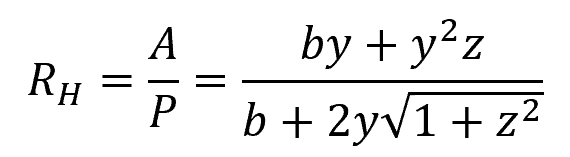
Where:
- b = bottom width of the channel [m]
- y = depth of flow [m]
- z = slope of the trapezoidal sides [unitless]
Hydraulic Radius of a Triangular Channel
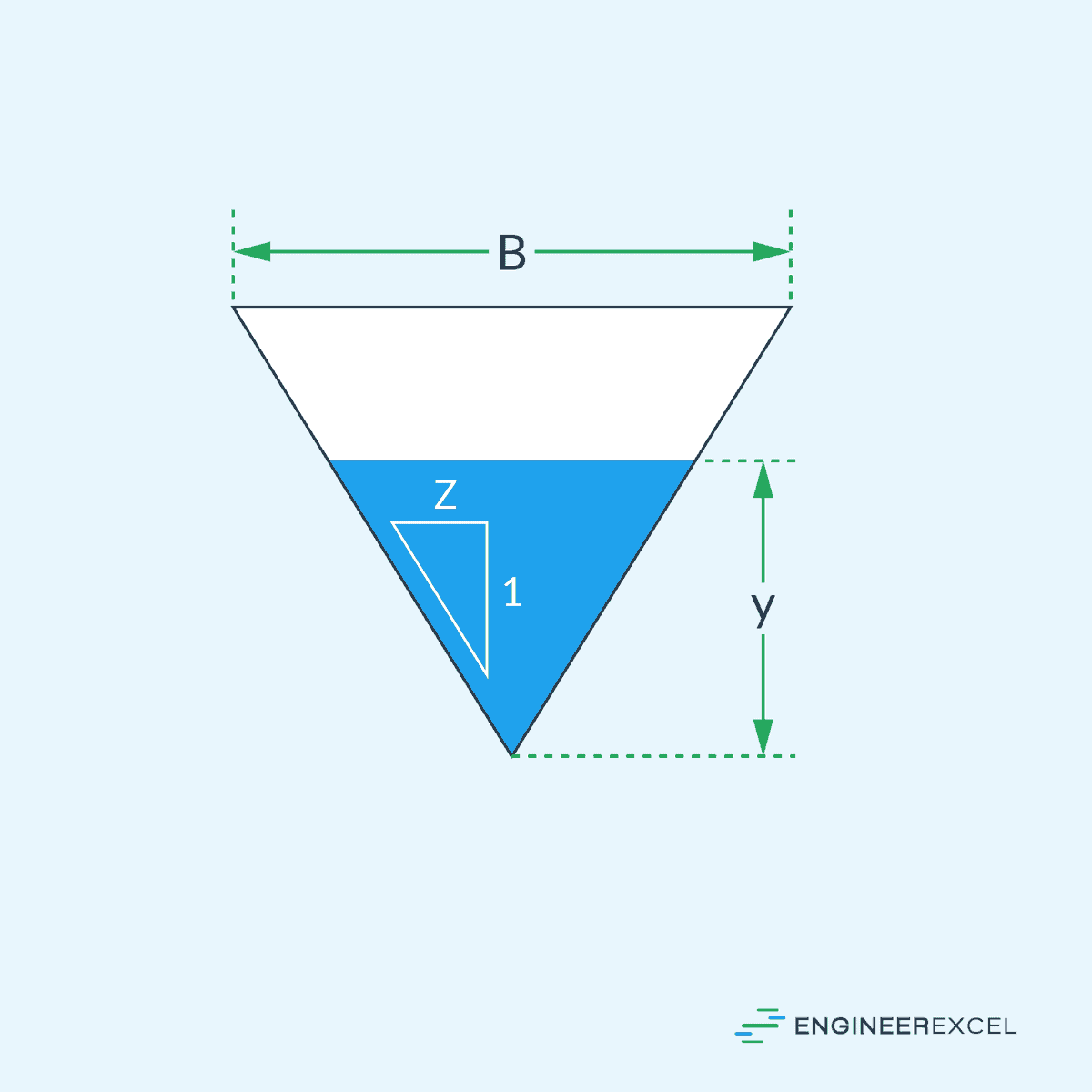
For a triangular channel, the hydraulic radius can be calculated using the following formula:
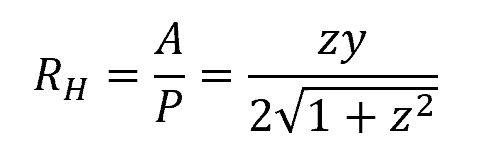
Where:
- z = slope of the triangular sides [unitless]
- y = depth of flow [m]
Hydraulic Radius of a Circular Channel
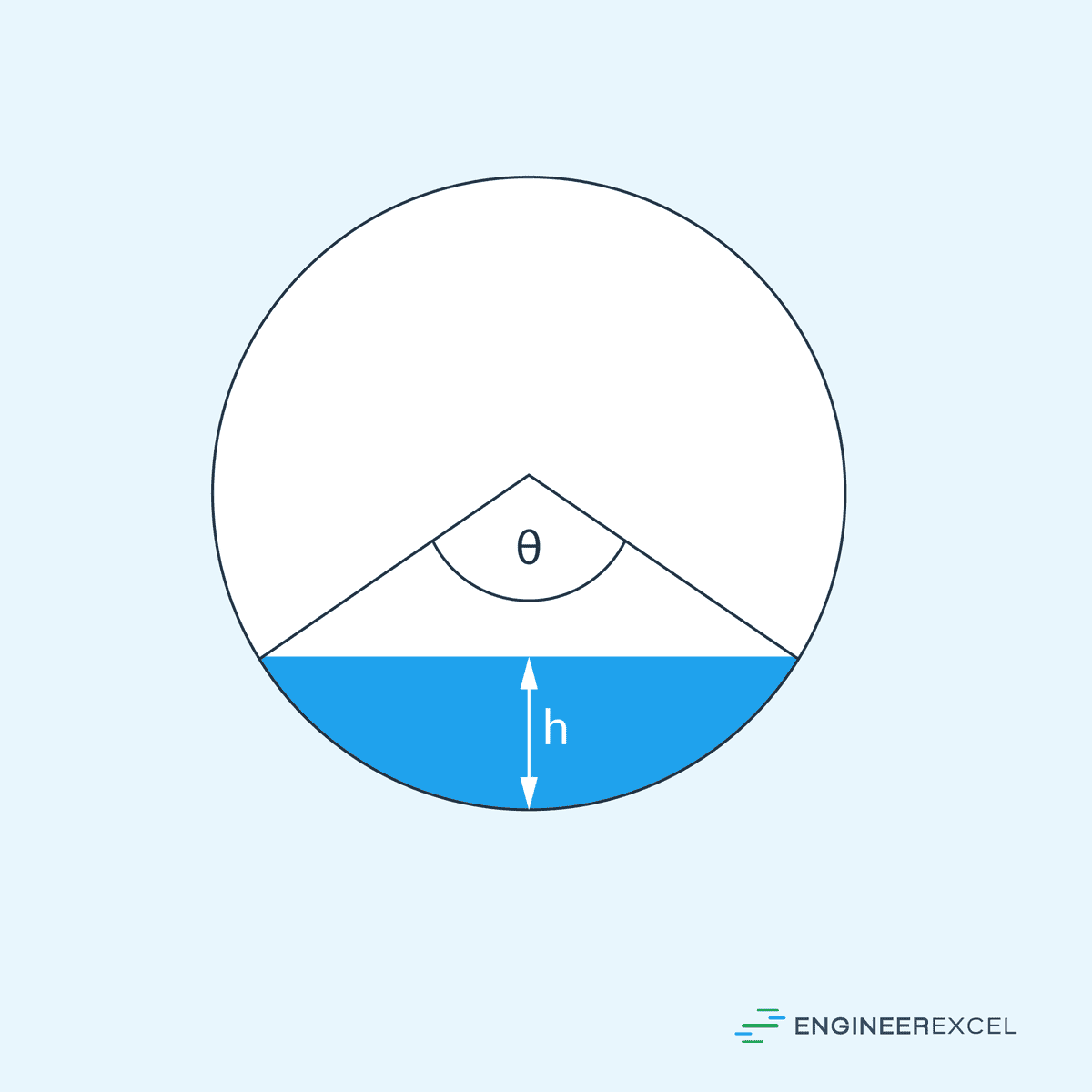
For a partially full circular channel, the hydraulic radius can be calculated using the following equation:

Where:
- r = radius of the circular channel [m]
- θ = central angle of the intercepted arc between the depth of flow and the channel [rad]
For a circular pipe running full, the hydraulic radius is simply equal to the pipe radius.
Hydraulic Radius of Irregular Sections
For irregular cross-sectional channels, one common method to compute the Hydraulic Radius is by using the concept of equivalent rectangular channels. The formula for the Hydraulic Radius remains the same; however, determination of the flow area and wetted perimeter involves creating an equivalent rectangular channel with the same hydraulic properties as the irregular channel. This process usually requires detailed survey data of the channel cross-section.
Another approach is to divide the irregular cross-section into smaller regular sections (e.g., triangles or trapezoids) and use numerical integration techniques to calculate the flow area and wetted perimeter. Once these values are obtained, the Hydraulic Radius can be calculated using the general formula.
Hydraulic Diameter
Hydraulic diameter is a closely related parameter to hydraulic radius. It is defined as the ratio of four times the cross-sectional area to the wetted perimeter, as shown in the following equation:
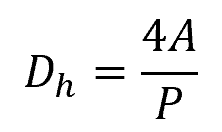
Where:
- Dh = hydraulic diameter [m]
Contrary to what the name implies, the hydraulic diameter is not just double the hydraulic radius, but rather four times larger:
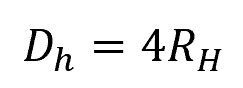
The concept of hydraulic diameter is particularly useful when dealing with complex geometries, such as rectangular or triangular channels, where a simple diameter may not be readily defined. It is commonly used in various engineering applications, including the calculation of Reynolds number, friction factor, and other dimensionless parameters that govern fluid flow and heat transfer. It allows engineers to apply relationships developed for circular pipes to non-circular geometries, facilitating the analysis and design of systems involving fluid flow.
Applications of Hydraulic Radius
Open Channel Flow
In open channel flow, the hydraulic radius plays an essential role in various hydraulic calculations. For instance, in the Chezy equation, it is utilized to determine the flow velocity along an open channel, as depicted by the following equation:
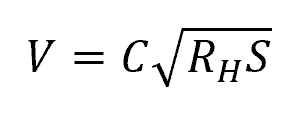
Where:
- V = flow velocity [m/s]
- C = Chézy coefficient [m1/2/s]
- S = slope of the energy grade line [unitless]
Similarly, it is employed in the Manning equation in a similar manner:

Where:
- n = Manning’s roughness coefficient [unitless]
Viscous Flow in Ducts
The hydraulic radius is also relevant in the analysis of viscous flow through ducts, such as pipes, conduits, and airways. By characterizing the flow conditions, the hydraulic radius helps in predicting the pressure drop, energy dissipation, and flow resistance in ducts.
For example, the Darcy-Weisbach equation that is used to calculate for the head loss due to friction in a pipe can be expressed as:
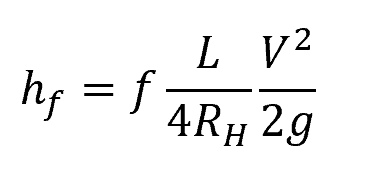
Where:
- hf = major head loss [m]
- f = friction factor [unitless]
- L = pipe length [m]
- g = acceleration due to gravity [9.81 m/s2]
Example Problem
Problem: A rectangular channel has a width (b) of 2 meters and a depth (y) of 1.5 meters. Calculate the hydraulic radius of the channel.
Solution: The hydraulic radius of a rectangular channel can be calculated using the following formula:
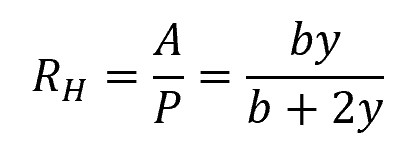
Plugging in the values:
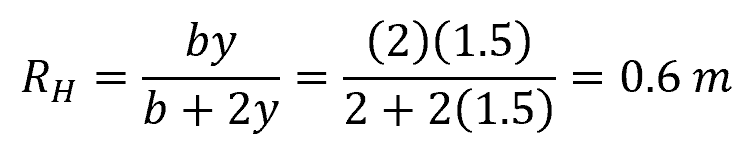
Therefore, the hydraulic radius of the rectangular channel is 0.6 meters.
