Subcritical flow occurs when the flow velocity of a fluid is less than the speed of a small surface wave. In this condition, the flow is relatively tranquil, and water particles move in a manner similar to the propagation of surface ripples.

In this article, we will discuss the classification of subcritical flow based on the Froude number, the distinction between subcritical and supercritical flow, and examples of subcritical flow in natural and man-made channels.
Understanding Subcritical Flow
Subcritical flow refers to a hydraulic condition in an open channel where the flow velocity is below the critical velocity, and the flow depth is above the critical depth. In this state, the water movement is dominated by gravitational forces and characterized by a gradual and stable flow pattern.
The general equation for determining critical depth for a given flow rate and channel geometry is:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
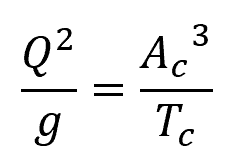
Where:
- Q = flow rate [m3]
- g = gravitational acceleration [9.81 m/s2]
- Ac = cross-sectional flow area [m2]
- Tc = width of the channel section at the free surface [m]
For irregular shapes, this equation can be solved by trial and error. However, for common shapes, the flow depth (yc) can be derived from Ac and Tc using geometric relations.
Once the critical depth is found, the critical velocity can be found by simply dividing the flow rate by the flow area:
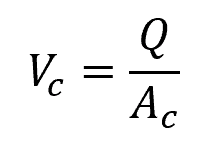
Where:
- Vc = critical flow velocity [m/s]
The critical velocity and critical depth mark the threshold where the flow transitions between subcritical and supercritical states.
In subcritical flow, the water surface slope is typically mild. The water moves slowly over a relatively flat channel bed, allowing for better sediment transport and facilitating the growth of river ecosystems. In contrast, the slope in supercritical flow is steep, leading to increased erosion and the formation of hydraulic jumps, where energy is rapidly dissipated through turbulence.
This is illustrated in the diagram below.

Froude Number for Subcritical Flow
The Froude number is a dimensionless number that represents the ratio of inertial forces to gravitational forces in fluid flow.
In the context of open channel flow, it is particularly useful for differentiating between subcritical and supercritical flow conditions. When the Froude number is less than 1, the flow is considered to be subcritical. This means that energy forces dominate the flow, and disturbances in the water surface travel faster than the flow velocity.
To calculate the Froude number (Fr), the following equation can be employed:

Where:
- V = flow velocity [m/s]
- Y = flow depth [m]
In subcritical flow, the celerity (c) or wave velocity relative to the medium) is greater than the flow velocity. This characteristic allows disturbances in the flow to propagate in both upstream and downstream directions, with the upstream disturbance traveling at a velocity of (V-c) and the downstream disturbance traveling at a velocity of (V+c), as shown in the diagram below.
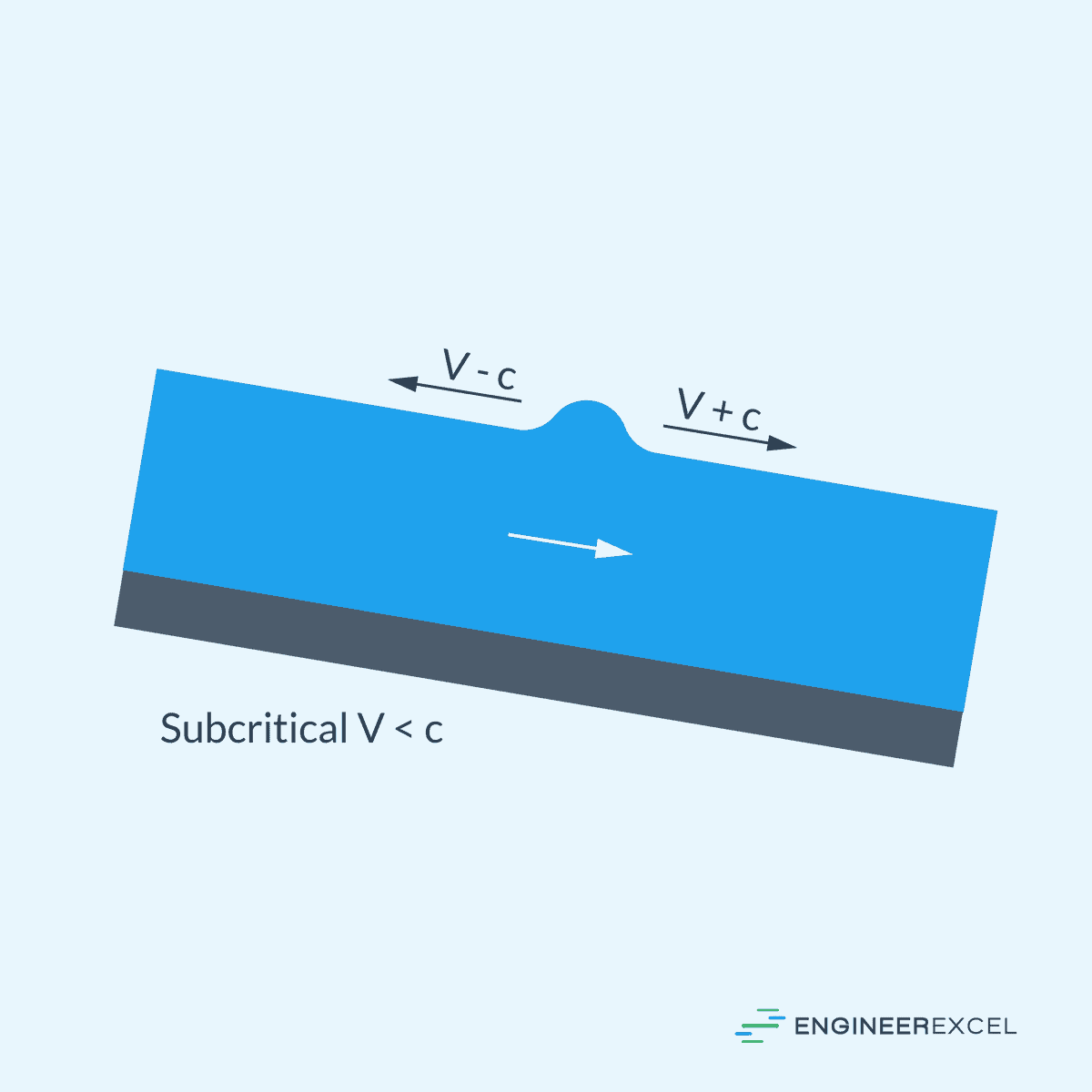
In this condition, the flow is subject to downstream control, meaning that the flow is controlled from a downstream point and information is transmitted upstream. This allows for the management and regulation of the flow from the downstream end, such as through the use of control structures like gates or weirs. This downstream control is essential for managing subcritical flow and mitigating any potential backwater effects.
Specific Energy of Subcritical Flow
Specific energy in open channel flow is the total energy per unit weight of fluid, comprising both kinetic and potential energy, as shown in the following equation:
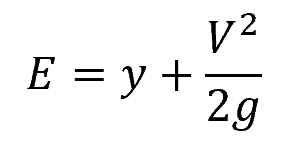
Where:
- E = specific energy [m]
The diagram below illustrates how the specific energy can be plotted against flow depth for a given discharge.
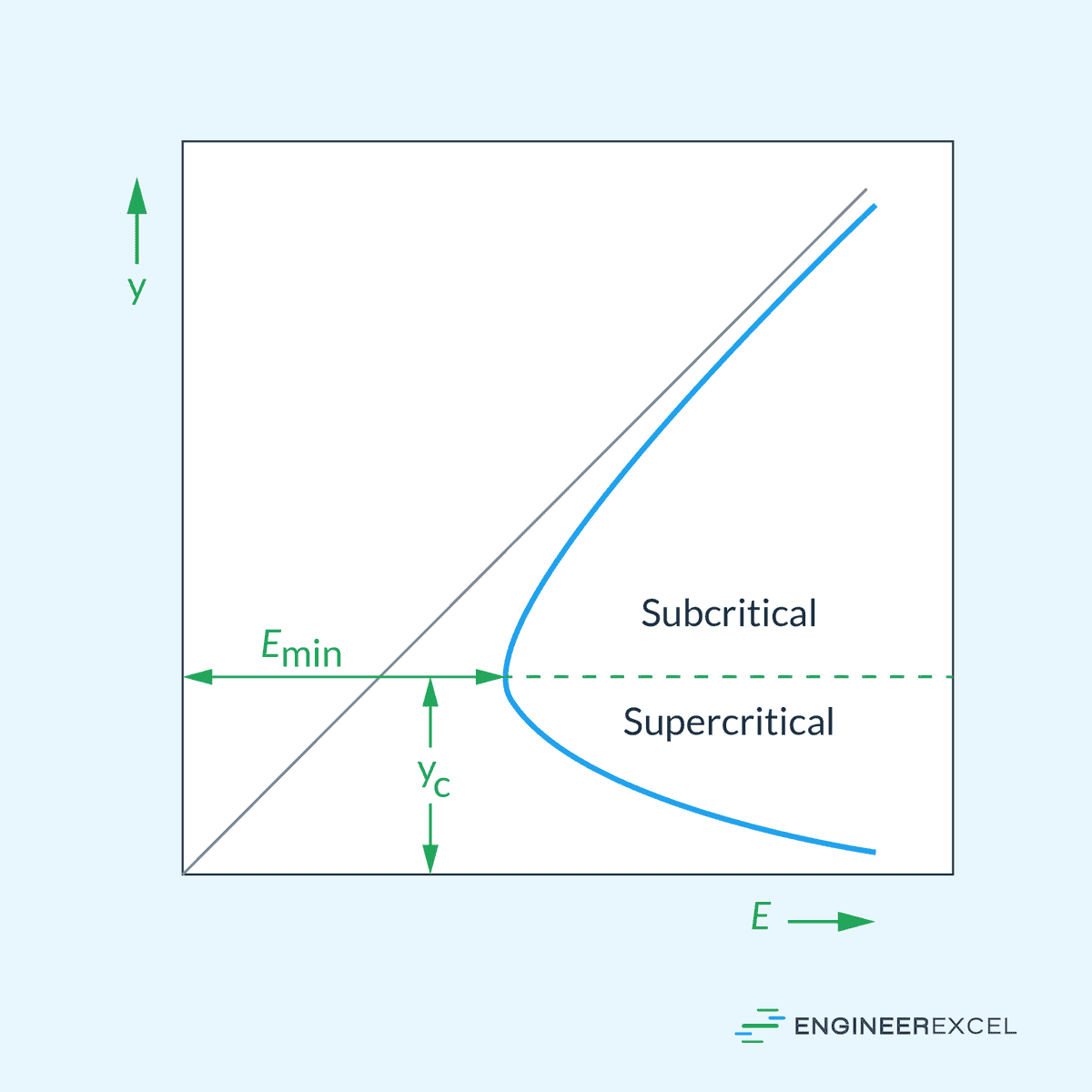
The subcritical region in this diagram is located above the critical point, marked by the point (Emin, yc), where the specific energy reaches its minimum value.
Examples of Subcritical Flow
Rivers and Streams
These natural watercourses typically exhibit subcritical flow. Due to their geometry, being wide and shallow relative to their length, rivers and streams tend to have a flow velocity that is less than the critical velocity.
Irrigation Canals
Another example is irrigation canals, which are designed to carry water with a gentle slope. Here, the engineers ensure that the flow remains subcritical to avoid structural damage from high-velocity flow and to provide a uniform distribution of water to farmlands.
Tidal Flows
While the sea surface may experience supercritical conditions, in areas where the tidal movement propagates into estuaries or coastal environments, the flow typically transitions to subcritical. This is due to the increasing breadth and decreasing depth, which dramatically reduces the flow velocity. For instance, in estuarine environments, tidal currents can be represented as follows:
Tranquil Flow in Man-made Channels
Engineers often seek to establish subcritical flow conditions in man-made channels for stability and to minimize erosion. Water treatment facilities also leverage subcritical flow states for controlled sedimentation processes.
Example Problem
Problem: A rectangular channel has a width (b) of 4 meters and a depth (y) of 2 meters. The flow rate through the channel is 10 cubic meters per second. Is the flow subcritical?
Solution:
The Froude number (Fr) in an open channel is given by the formula:

First, we need to calculate the flow velocity (V) using the flow rate and channel dimensions:
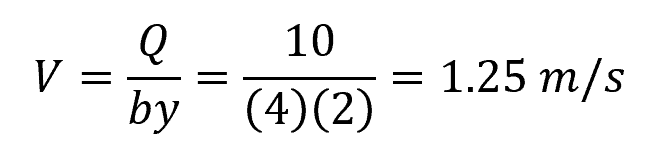
Now, we can calculate the Froude number using the flow velocity and flow depth:
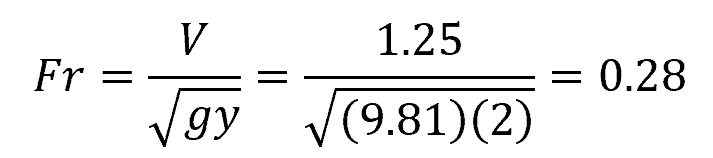
Since the Froude number is less than 1, therefore, the flow is subcritical.
