Uniform flow in open channels refers to a steady and constant flow condition where the water velocity, depth, and channel slope remain constant along a particular reach. In uniform flow, the gravitational and frictional forces acting on the water are balanced, resulting in a consistent and predictable flow pattern.

In this article, we will discuss the characteristics and analysis of uniform flow in open channels, including the flow resistance equations, normal depth calculation, and real-world applications of uniform flow.
Uniform Flow Explained
Uniform flow in open channels describes a condition where the depth and velocity of the water remain constant along the length of the channel, as shown in the diagram below. This steady state occurs when the forces propelling the water downstream, primarily gravity, are in equilibrium with forces resisting the flow, such as channel friction.


Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
When an open channel has a consistent cross-sectional shape and bottom slope, it facilitates a scenario where the water’s velocity no longer accelerates or decelerates. This state results from the balance between gravitational forces driving the flow and the resistance exerted by the channel boundaries due to shear stress.
In steady, uniform flow, both the local and convective accelerations are zero. Hence, the equation of motion becomes:
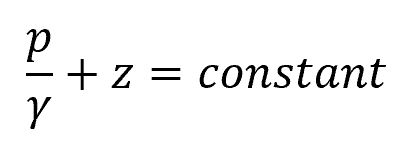
Where:
- p/γ = pressure head [m]
- z = elevation head [m]
It is important to note that uniform flow is an ideal state and natural channels may only approximate this condition in certain stretches. In real-world applications, engineers often make simplifications for one-dimensional analysis of such flows, disregarding the complex behaviors like secondary currents and variable shear resistance. In practice, open channels can have varying geometries and roughness, so achieving uniform flow may necessitate channel design that approximates these ideal conditions.
Flow Resistance Equations in Uniform Flow
Flow resistance equations provide the basis for calculating the flow rate given channel geometry and roughness characteristics of a uniform flow. The most widely used equations in uniform flow analysis are Manning’s Equation, Chezy’s Formula, and the Strickler Equation.
Manning’s Equation
Manning’s equation is a widely accepted empirical formula that relates the flow rate, cross-sectional area, hydraulic radius, and channel slope to the roughness coefficient of the channel. The equation in its most common form in SI units is:

Where:
- Q = flow rate [m3/s]
- n = Manning roughness coefficient [unitless]
- A = cross-sectional area [m2]
- Rh = hydraulic radius [m]
- So = slope of the channel [unitless]
Note that the hydraulic radius is the cross-sectional area of the flow divided by the wetted perimeter.
The Manning roughness coefficient is dependent on the surface characteristics of the channel, including the roughness of the channel bed and the presence of vegetation or other obstructions. It is influenced by factors such as the type of material in the channel, the presence of sediment, and the overall condition of the channel’s lining. The table below lists the typical Manning roughness coefficient for different channel linings.
Chezy’s Formula
Chezy’s formula is an earlier form of the Manning’s equation. It states that flow velocity is proportional to the square root of the product of the hydraulic radius and the channel slope, and inversely proportional to the Chezy coefficient. The formula can be represented as:

Where:
- V = flow velocity [m/s]
- C = Chézy coefficient [m1/2/s]
The Chezy coefficient remains constant for a given channel shape and bottom roughness, and it is linked to the friction factor through the following equation:
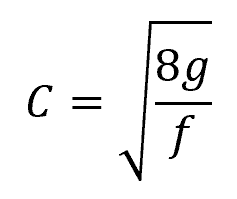
Where:
- g = gravitational acceleration [9.81 m/s2]
- f = friction factor [unitless]
Strickler Equation
The Strickler Equation is another empirical relation, popular in Europe, that is used to estimate uniform flow velocity. The flow velocity according to Strickler is given by:
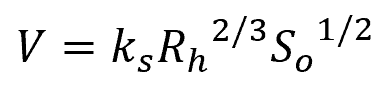
Where:
- ks = Strickler constant
The Strickler constant can be computed using the following equation:

Where:
- k = mean size of the wall roughness [mm]
The roughness sizes (k) for different materials are listed in the table below.
It is interesting to note that the Manning and Strickler equations are actually similar and that their coefficients are simply the inverse of each other.
Normal Depth Calculation for Uniform Flow
Uniform flow in an open channel occurs when the depth and velocity of the water remain constant along the length of the channel. The normal depth is the depth at which this uniform flow occurs and is denoted as (yn).
To calculate the normal depth, for a specified discharge (Q), Manning’s n, and the bottom slope (So), the Manning’s Equation can be rearranged as follows:
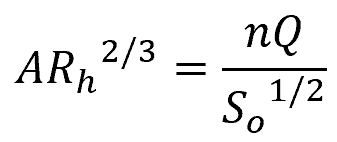
The left-hand side of the above equation is called the section factor. Using this equation, the normal depth is found iteratively, either graphically or numerically, until the discharge calculated from the assumed depth matches the specified discharge,
Real-World Applications of Uniform Flow
Uniform flow in open channels underpins several key engineering and environmental processes, facilitating the design and analysis of hydraulic structures and natural water bodies. One of the primary applications is in the design of irrigation canals, where it is important to ensure a steady, uniform flow for efficient water delivery to agricultural lands. The concept of uniform flow allows for the prediction and control of water depth and velocity, thus optimizing irrigation and minimizing water waste.
Another critical application is found within the urban environment, specifically in the design of stormwater drainage systems. These systems rely on the principles of uniform flow to ensure that runoff is conveyed away from urban areas efficiently to reduce the risk of flooding.
Lastly, water treatment facilities utilize uniform flow conditions in sedimentation basins where suspended particles are allowed to settle out by gravity. A uniform flow regime ensures that flow velocities are sufficiently low to prevent resuspension, which is critical for effective purification of the water.
