The wetted perimeter is the length of the interface between a flowing fluid (such as water in a river or stream) and the channel or bed it is flowing through. It plays an important role in hydraulic and fluid dynamics calculations, influencing factors like friction and resistance to flow in open channels.

In this article, we will discuss the calculation of wetted perimeter for different channel cross-sections, its significance in calculating hydraulic radius and equivalent Manning constant, and the various techniques for measuring wetted perimeter in hydraulic engineering.
Wetted Perimeter Explained
The wetted perimeter is the length of the interface between a fluid (e.g., water) and the channel, pipe, or structure through which the fluid flows. In the context of rivers, streams, and open channels, it encompasses the portion of the channel bed and banks in contact with the flowing water. This parameter is significant in hydraulic and hydrological calculations as it impacts flow resistance and factors like frictional losses.
The formula for calculating the wetted perimeter depends on the shape of the channel’s cross-section.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
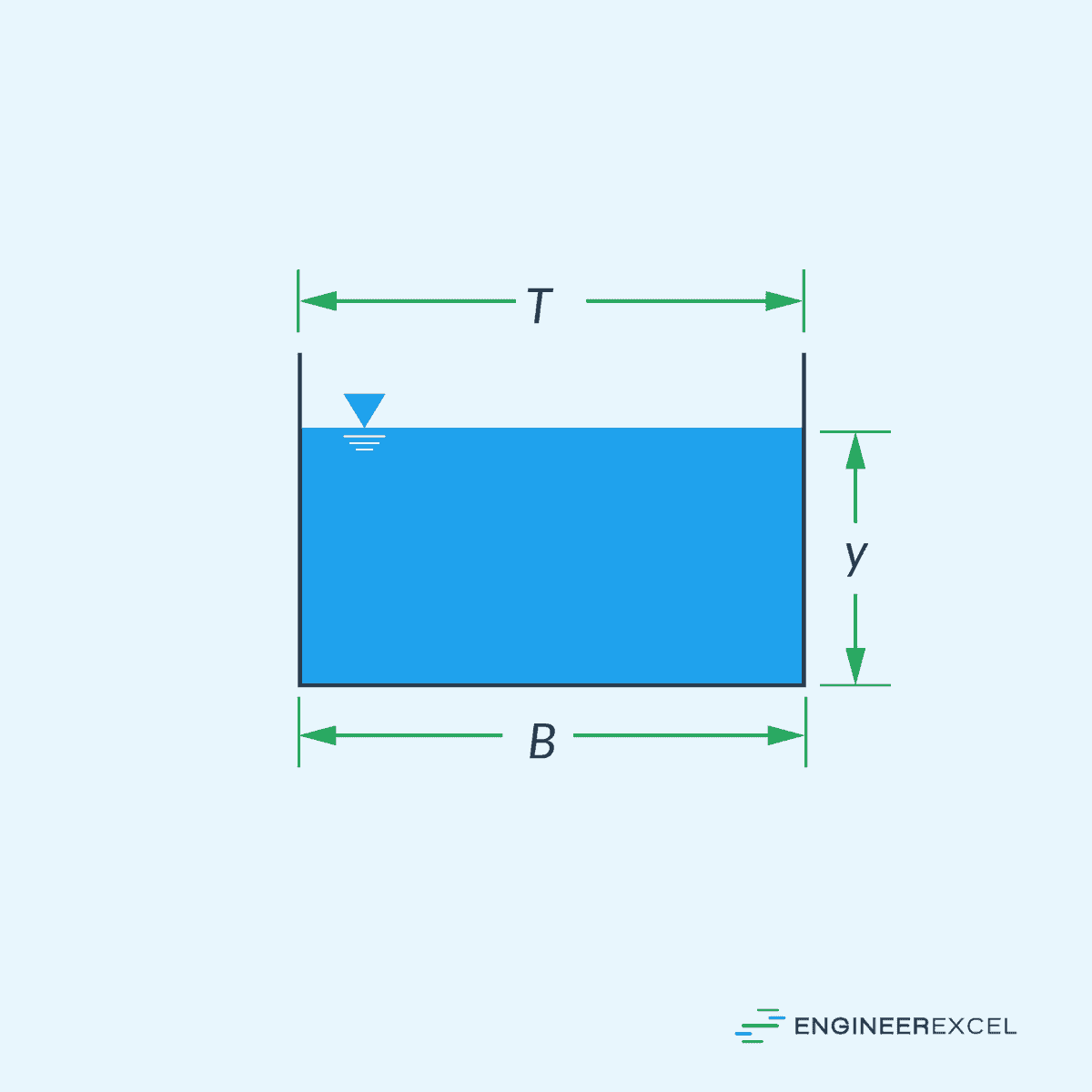
For example, for a rectangular channel, the wetted perimeter can be calculated using the following formula:
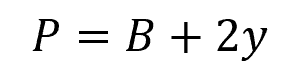
Where:
- P = wetted perimeter [m]
- B = width of channel bottom [m]
- y = depth of fluid [m]
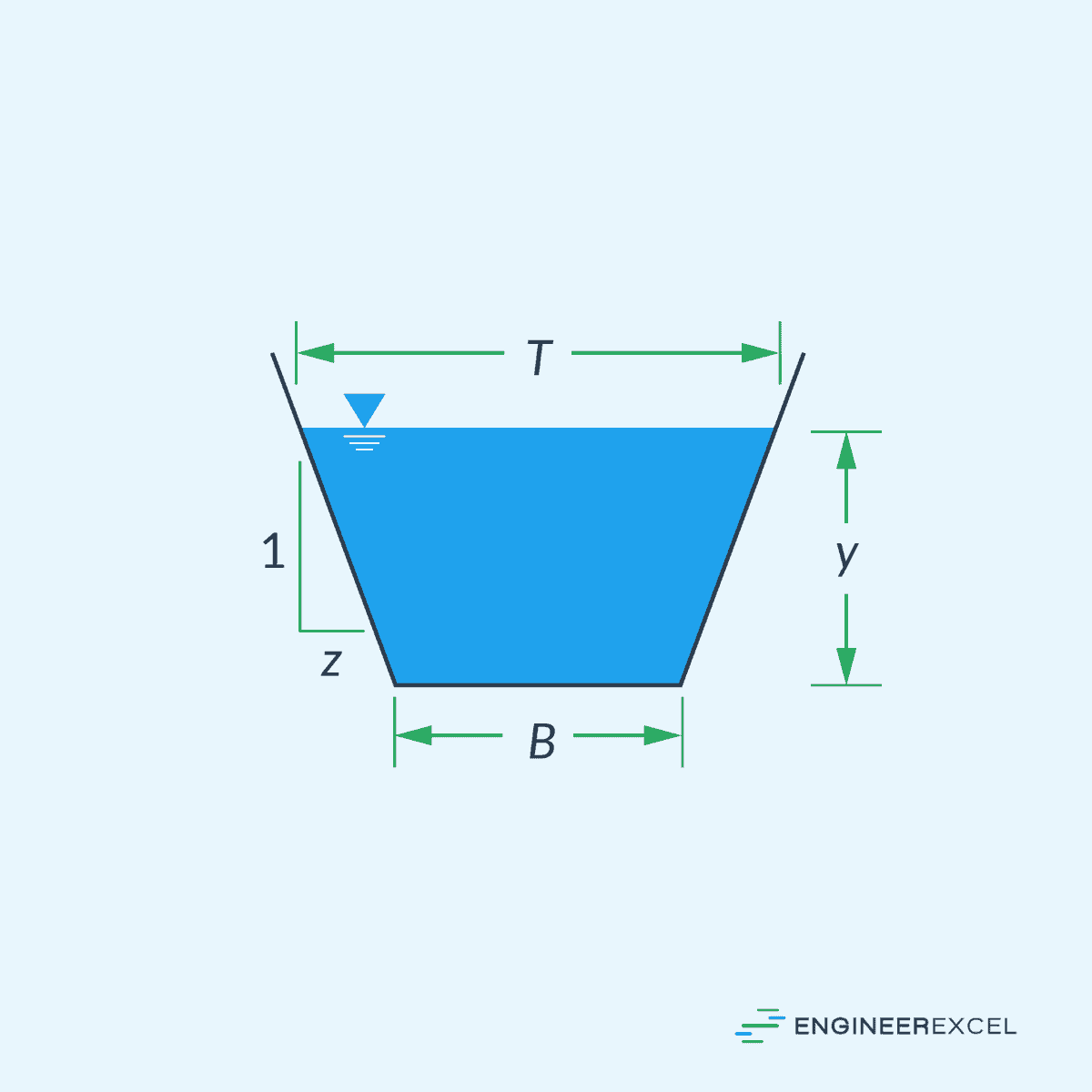
For a trapezoidal channel:
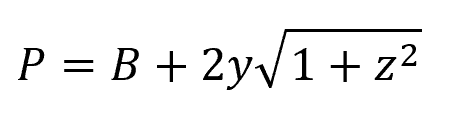
Where:
- z = slope of the sides of the channel [unitless]
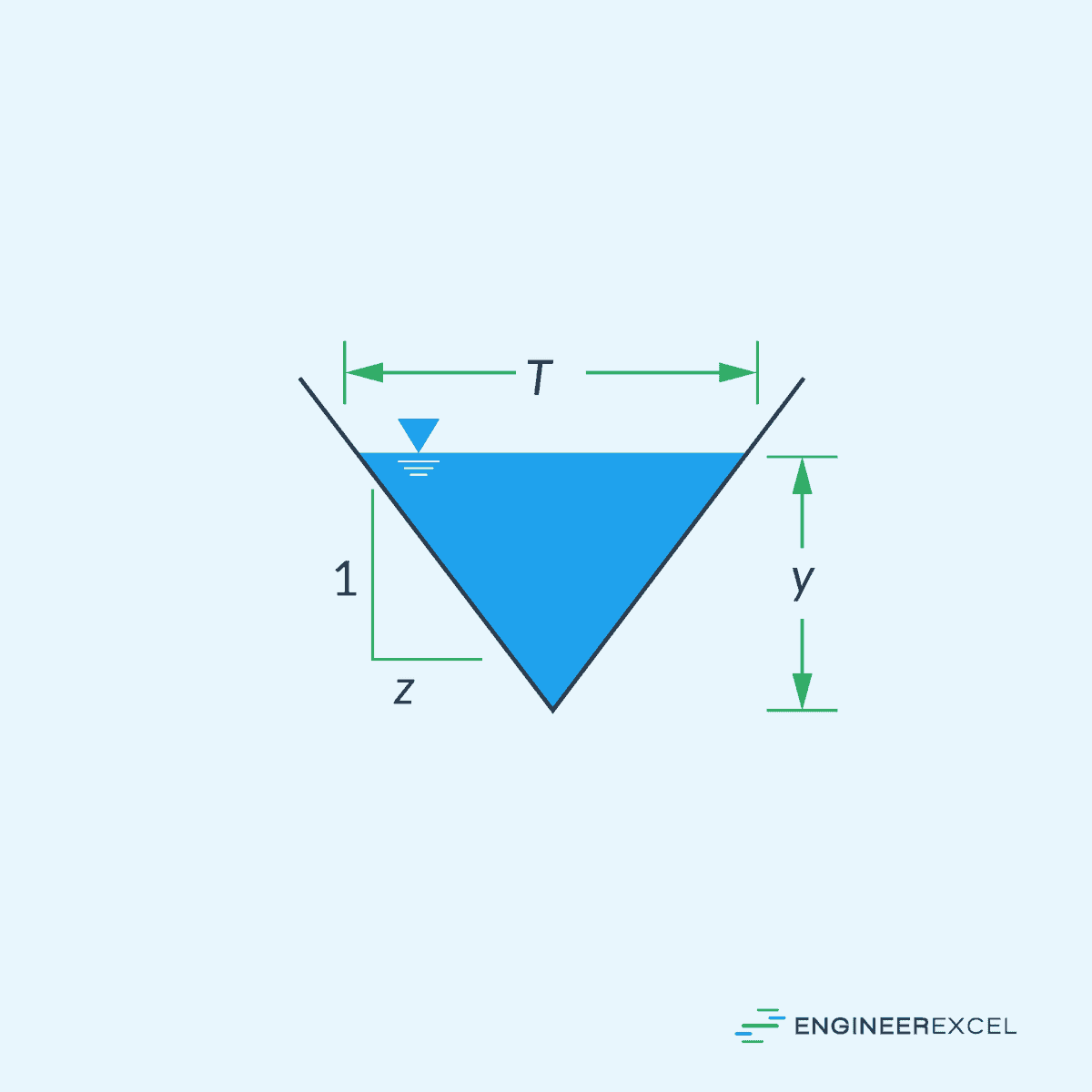
For a triangular channel:
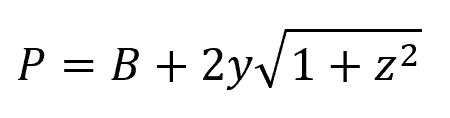
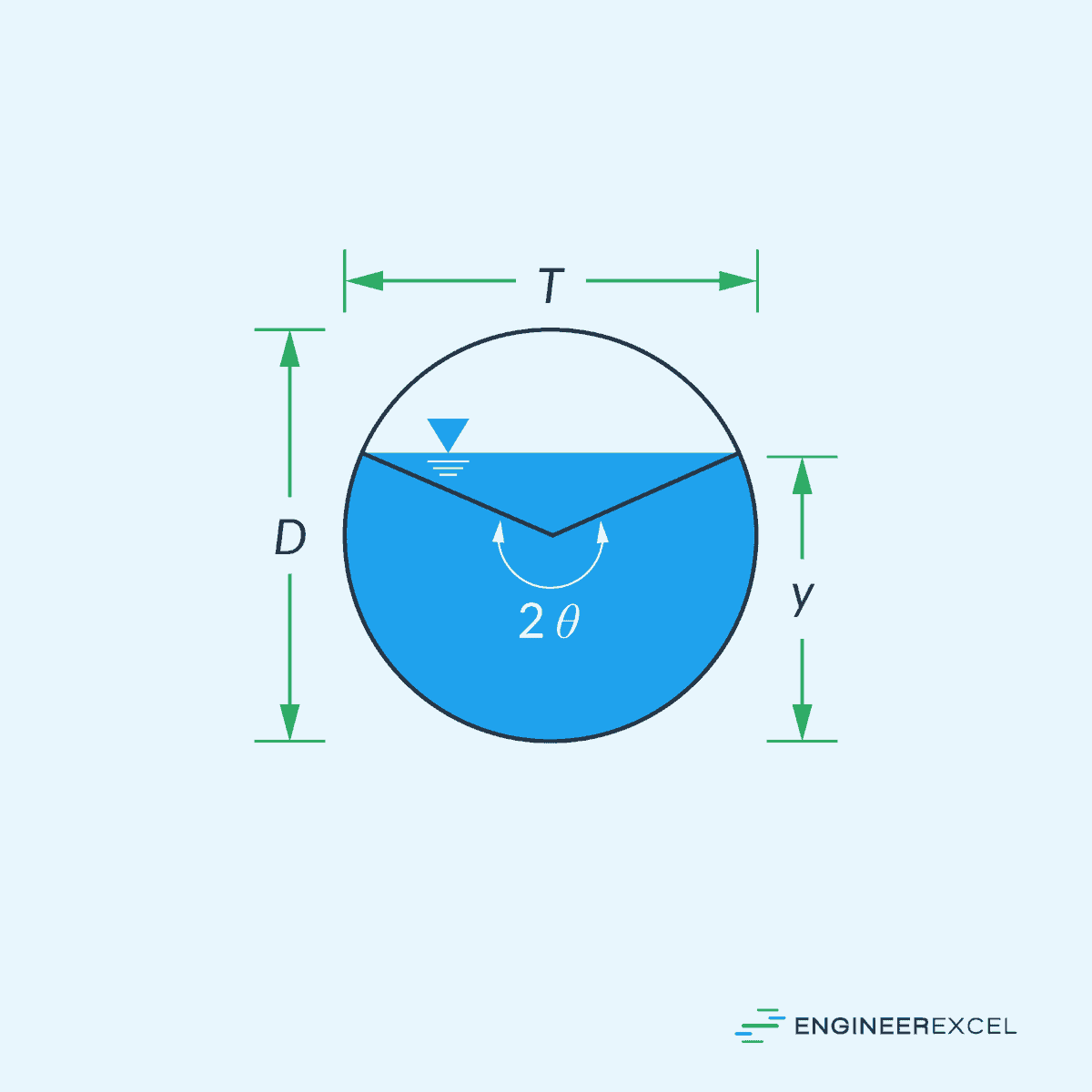
And for a circular channel, such as a pipe:
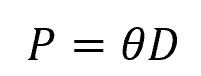
Where:
- θ = half angle of the intercepted arc between the depth of flow and the channel [rad]
- D = diameter of the circular channel [m]
For irregular shapes, calculating the wetted perimeter typically requires integrating the length of the channel’s boundary that is in contact with the fluid. This can involve more complex mathematical methods such as using planimeter measurements or applying numerical integration techniques when dealing with a natural river course or streambed.
Hydraulic Radius
One of the key uses of wetted perimeter is calculating the hydraulic radius.
The hydraulic radius is a parameter used in fluid mechanics to characterize the efficiency of an open channel in conveying flow. It is defined as the cross-sectional area of flow divided by the wetted perimeter, expressed by the formula:
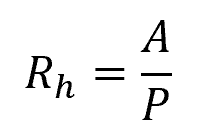
Where:
- Rh = hydraulic radius [m]
- A = cross-sectional area of flow [m2]
In terms of hydraulic efficiency, a larger hydraulic radius suggests a more efficient flow with less resistance from friction. Hence, channels are often designed to maximize the hydraulic radius, making the flow more efficient for a given cross-sectional area.
Engineers use the hydraulic radius in calculations like the Manning equation and the Reynolds number, which are essential for the design and analysis of open channels and pipes. For example, in the Manning equation, the hydraulic radius is used to calculate the flow rate by considering channel slope and roughness coefficient.
It is important to note that the hydraulic radius does not have a physical presence; rather, it is an indicative measure that influences and describes flow characteristics in engineering applications.
Equivalent Manning Constant
The wetted perimeter also has an important role in determining flow resistance parameters, such as the equivalent Manning constant.
The Manning constant (n) is a coefficient derived from empirical data and varies based on the roughness of the channel’s surface material. It is generally assumed that the Manning constant is uniform along the channel, allowing the Manning equation to be directly used for calculating flow velocity and rate. However, this assumption may not always hold true.
For instance, if the channel bottom and sides are made from different materials, their Manning constants may differ. In such cases, it’s essential to determine an equivalent Manning constant for the entire cross section.
For a channel section divided into N subareas with different roughness levels, the equivalent Manning constant can be calculated using the following equation:
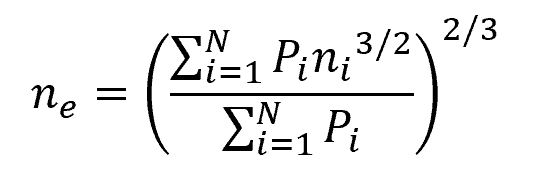
Where:
- ne = equivalent Manning constant [unitless]
- N = number of subareas with different roughness levels [unitless]
- Pi = wetted perimeter for each subarea [m]
- ni = corresponding Manning constant for each subarea [unitless]
The above equation assumes that the mean flow velocity in each subarea equals that of the entire section.
Measuring Wetted Perimeter
Accurate wetted perimeter measurement is critical in hydraulic engineering for determining flow characteristics in open channels. The techniques vary in complexity and precision, depending on the environment and resources available.
Direct Measurement
Direct measurement involves physically touching the boundary that the fluid is in contact with using tools such as measuring tapes or graduated staffs to determine the length. For irregular surfaces, such as natural streams, a surveyor might use a chain or rope that conforms to the contours of the channel bed and banks. The chain is then straightened, and the length corresponding to the wetted perimeter is measured.
Cautions are necessary to ensure accuracy. It’s imperative to keep the measuring device taut to avoid sagging and inaccurate readings. Moreover, direct measurement can be time-consuming and may not be feasible for larger or inaccessible channels.
Indirect Assessment
Indirect assessment techniques estimate the wetted perimeter using mathematical models or by measuring other parameters that can be used to infer the perimeter. Hydrologists might use flow velocity and channel dimensions to calculate the wetted perimeter through empirical formulas where direct measurement is unachievable.
An example is using a velocity-area method where flow velocity measurements across the cross-section are used alongside the cross-sectional area to deduce the wetted perimeter. Another approach involves photogrammetry or remote sensing technology to capture data and subsequently utilize geometrical calculations to estimate the perimeter.
Care must be taken when selecting the appropriate model or approach as errors in estimation can significantly impact the results of fluid dynamics calculations. The use of reliable data and validation against direct measurements ensures a higher degree of confidence in the indirect assessment results.
