Bending stress concentration occurs when a structure with sudden changes in cross-section undergoes bending, leading to localized areas of increased stress. Engineers must consider and mitigate these stress concentrations to ensure the structural integrity of a component under bending loads.

In this article, we will explore how bending stress concentration affects the structural integrity of materials, and how to calculate the maximum bending stress for various geometrical discontinuities.
Bending Stress Concentrations Explained
When a force or bending moment is applied to a structural component, such as a beam, it can cause the material to flex. This leads to stresses within the material, with one side in compression and the other in tension.
For simple beams under bending, the distribution of bending stress is typically linear, as shown in the diagram below. The maximum tensile and compressive stresses occur at the outermost fibers of the beam, farthest from the neutral axis. As you move towards the neutral axis, the stress decreases until it reaches zero.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
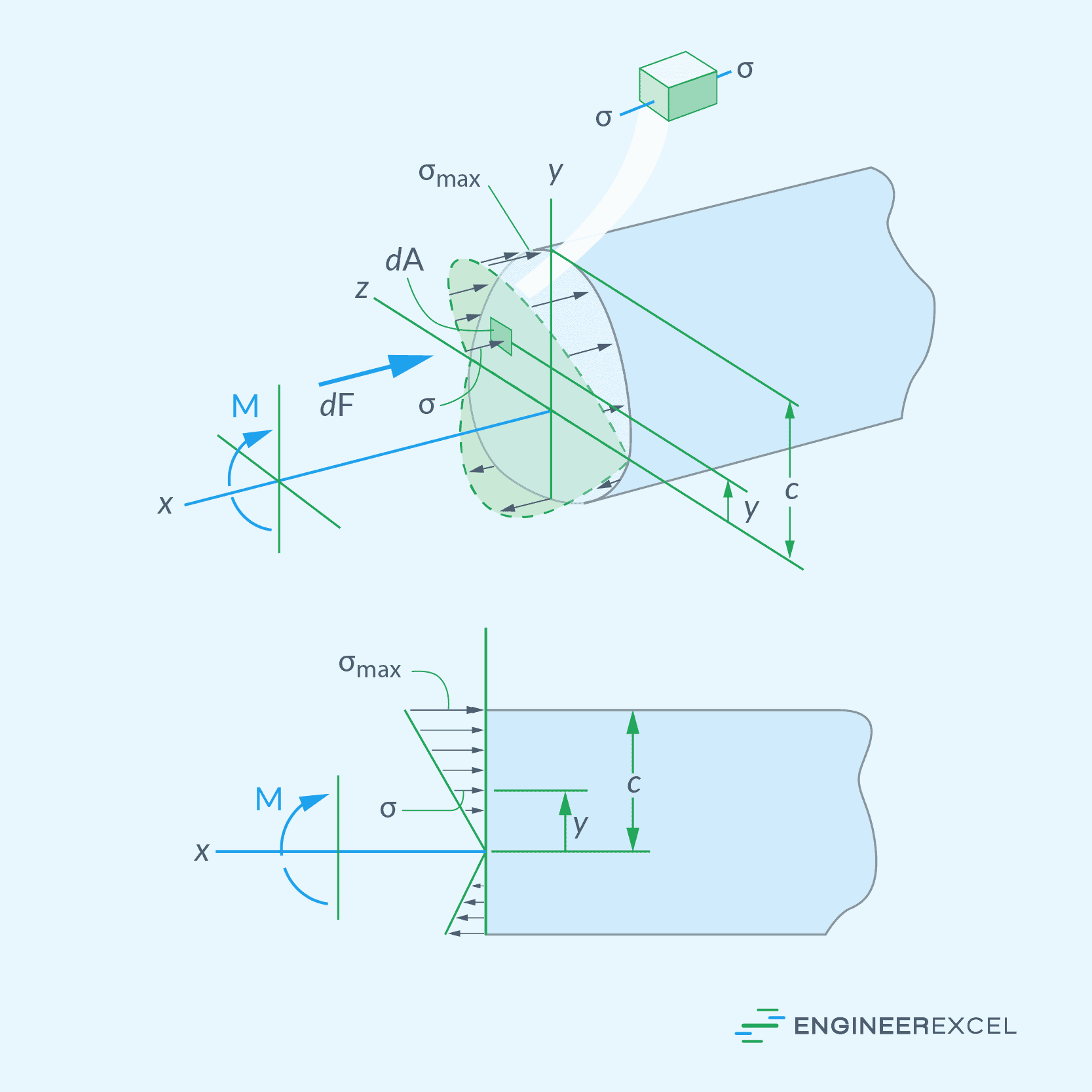
The bending stress formula is used to describe this distribution as follows:
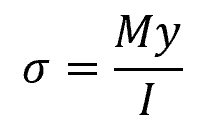
Where:
- σ = normal stress due to bending [Pa]
- M = applied bending moment [N-m]
- y = distance from the neutral axis to the point at which the stress is being calculated [m]
- I = moment of inertia [m4]
However, if the beam contains regions where the cross-sectional area suddenly changes, the stress at these sections is heightened and the stress distribution becomes more complex. This is what we refer to as bending stress concentration. The more severe the change, the larger the stress concentration.
Bending stress concentration occurs in common geometrical discontinuities, such as notches on a beam’s surface, holes for passage of fasteners, and abrupt changes in the outer dimensions of a beam. The increased levels of bending stress at these sections can negatively affect the structural integrity of the material. Hence, understanding stress concentrations is essential for optimizing the performance and longevity of various engineering applications.
Calculating Maximum Bending Stress Concentration
For design, it is generally important to only know the maximum normal bending stress developed at a discontinuity, not the actual stress distribution. This occurs at the section taken through the smallest cross-sectional area, which can be obtained using the following formula:

Where:
- K = bending stress concentration factor [unitless]
The bending stress concentration factor is a dimensionless parameter used to quantify the ratio of the maximum stress in the region of discontinuity to the average or nominal stress. Its value is generally determined through experiment and is only a function of the geometry of the discontinuity.
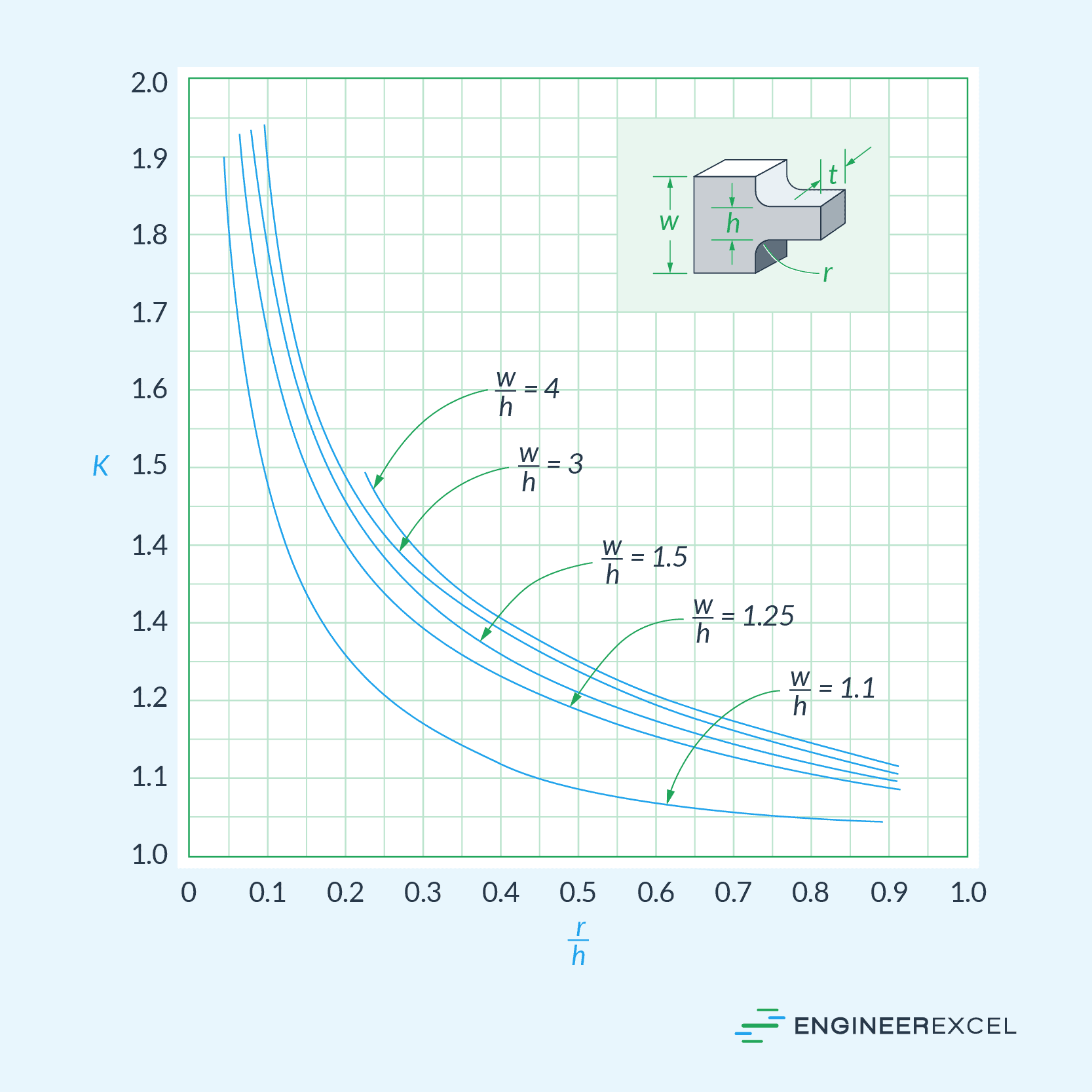
Bending Stress Concentration Factors
As an example, the graph below shows the stress concentration factor for flat bars with a change in cross section using shoulder fillets. Notice that its value depends on geometric ratios, specifically the ratio between the dimensions of the larger and smaller sections, as well as the ratio between the fillet radius and width of the smaller section.
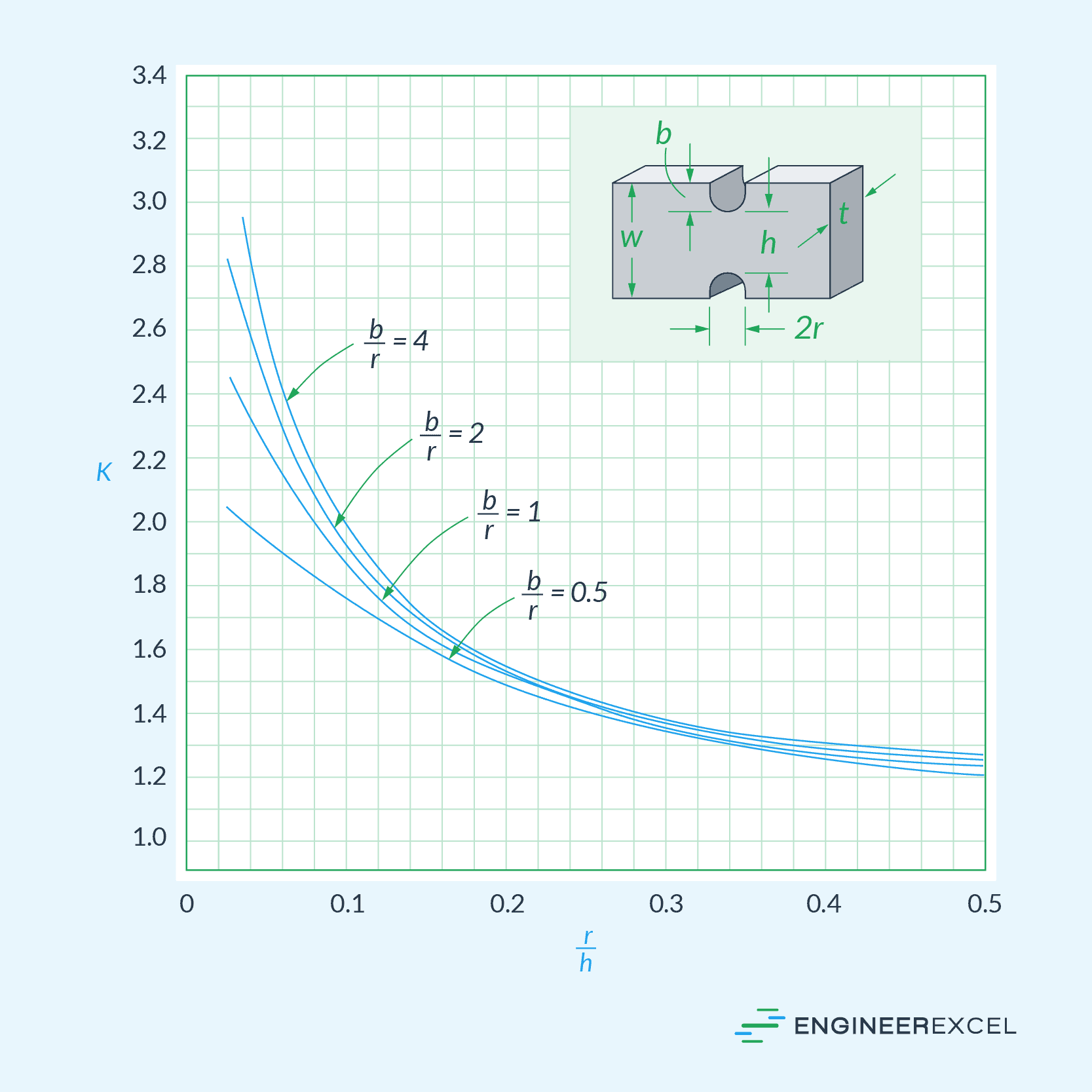
For circular grooves or notches, the stress concentration factor is given by the graph below. In this case, the value of the stress concentration factor depends on the ratio between the notch depth and notch radius, as well as the ratio between the notch radius and height of the smallest cross-section.
Applications of Bending Stress Concentration
Stress concentration in ductile materials under static moment typically does not need to be considered in design. However, when designing structures made of brittle materials or those under fatigue loading, it is important to consider the effects of stress concentration, as they are more susceptible to failure at these discontinuities.
The bending stress concentration factor is a key parameter used to quantify the degree of stress concentration in a material. However, it is important to note that the stress concentration factor only applies when the material is under elastic behavior. If the applied moment causes yielding of the material, the stress is redistributed throughout the member, resulting in a lower maximum stress than what would be determined using stress concentration factors.
