In solid mechanics, theories of failure are mathematical models used to predict the point at which a material or structure will fail under applied loads. For ductile materials, one of the most commonly used theories is the von Mises yield criterion, which states that failure occurs when the distortion energy per unit volume of a material equals or exceeds the distortion energy per unit volume of the same material when it is subjected to yielding in a simple tension test.

In this article, we will discuss the von Mises yield criterion in detail and how it can be used to predict material failure.
Understanding the von Mises Yield Criterion
In engineering design, it is important to set a limit on the state of stress that defines a material’s failure. For example, if the material is ductile, yielding usually indicates failure.
This is easy to determine in a uniaxial state of stress, like simple tension. However, if the member is under biaxial or triaxial stress, it is harder to establish the failure criterion. Hence, the theories of failure have been developed.
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
To use a specific theory of failure, you need to calculate the normal and shear stress at points where they are highest in the member. Then, determine the principal stresses at these critical points since each theory is based on this information. For ductile materials, one of the most often used failure theory for members under multiaxial stress is the von Mises yield criterion.
The Von Mises yield criterion, also known as the maximum distortion energy criterion, octahedral shear stress theory, or Maxwell-Huber-Hencky-Von Mises theory, states that failure occurs when the energy of distortion reaches the energy for yield in uniaxial tension tests.
Strain Energy Density
To better understand the von Mises yield criterion, it is important to know the concept of strain energy density.
When a material is subjected to external loading, it deforms and stores energy internally throughout its volume. The energy per unit volume of material is referred to as the strain energy density. If the material is under triaxial stress, each principal stress contributes to the total strain energy density, which can be calculated using the following formula:
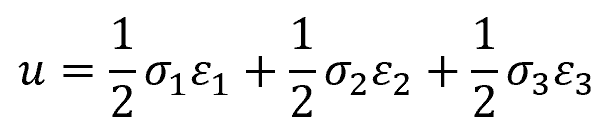
Where:
- u = strain energy density [Pa]
- σ1, σ2, σ3 = principal stresses [Pa]
- ε1, ε 2, ε 3 = principal strains [unitless]
This strain energy density can be divided into two parts. One part represents the energy from the average principal stress that causes a change in volume of the element (with no change in shape). The second part represents the energy that arises from the difference in magnitude between the principal stresses and the average stress, which causes distortion in the shape of the element.
This distortion energy can be calculated per unit volume using the following formula:
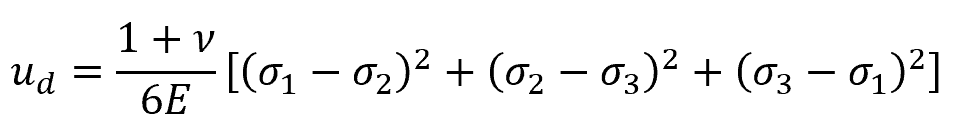
Where:
- ud = distortion energy per unit volume [Pa]
- ν = Poisson’s ratio [unitless]
- E = Young’s modulus [Pa]
Experimental evidence has shown that materials do not yield when subjected to a uniform hydrostatic stress, such as the average principal stress. Hence, yielding in a ductile material is caused by the distortion energy alone. This is the basis of the von Mises criterion.
Equation for von Mises Yield Criterion
The von Mises yield criterion predicts failure when the distortion energy per unit volume is equal to the distortion energy per unit volume in the tensile test specimen at failure, such that:

Where:
- σy = yield strength of the material [Pa]
In terms of principal stresses, this can be written as:
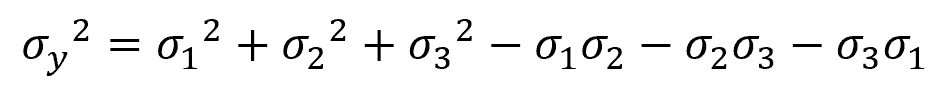
In general, the von Mises criterion has a better correlation with experimental results than other theories like the Tresca criterion, especially in pure shear conditions.
Von Mises Yield Criterion for Plane Stress
For plane stress, such that σ3 = 0, the von Mises criterion can be simplified into the following equation:
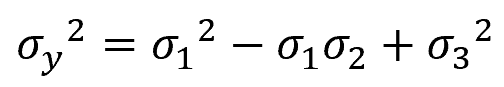
This can be graphically represented as an ellipse, as shown in the diagram below.
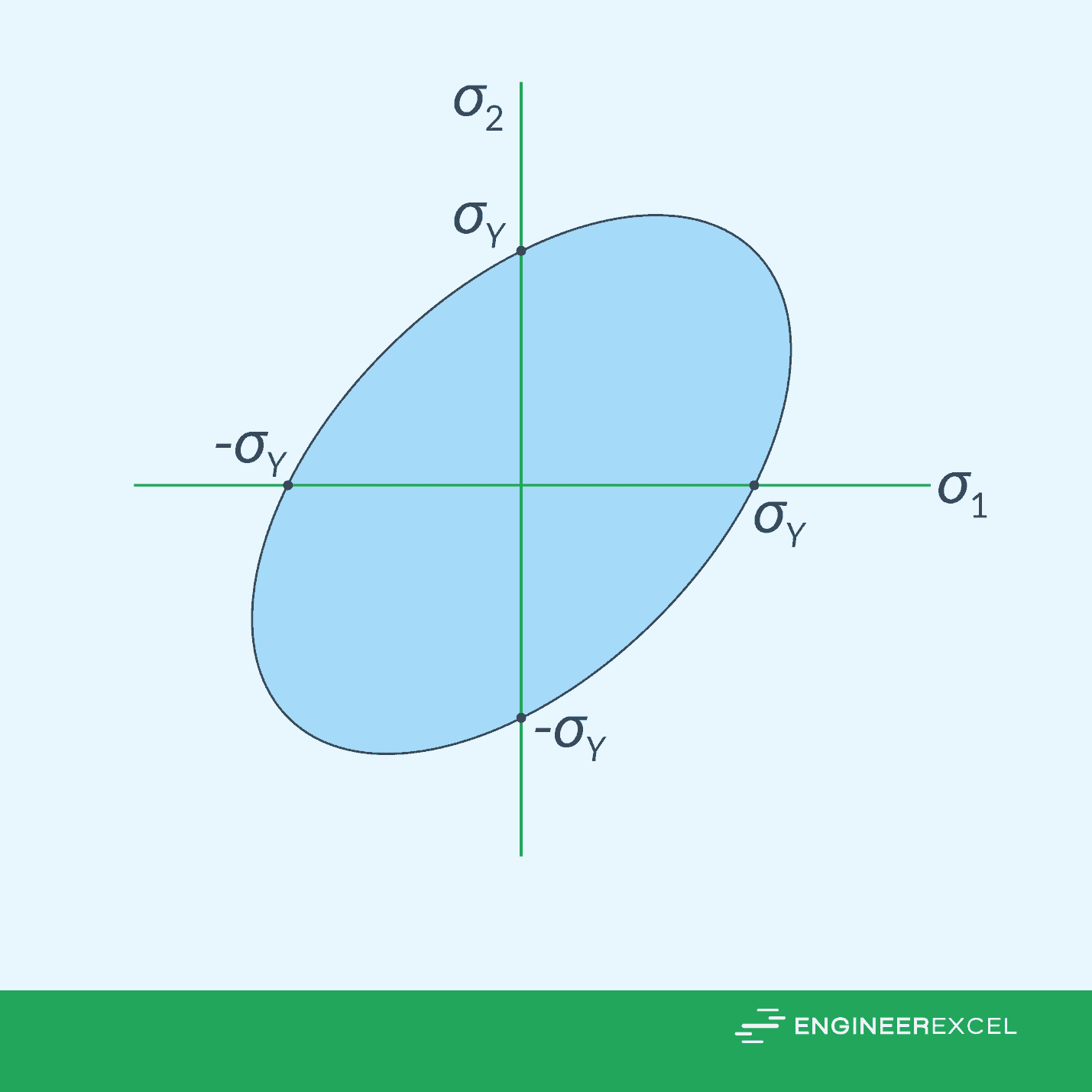
If a point in the material is stressed such that its principal stresses (σ1, σ2) fall on the boundary or outside the shaded area of the ellipse, the material is considered to have failed.
