The modulus of elasticity of concrete is a crucial property that measures the relationship between stress and strain in concrete when an external force is applied. It’s also known as the elastic modulus and plays a significant role in structural design as it helps predict the behavior of concrete under different loading conditions.

Read on to learn about the factors that affect the modulus of elasticity and its impact on structural design.
Concrete Modulus of Elasticity
Concrete is a composite material comprising cement, fine aggregates (sand), coarse aggregates, and water. Cement acts as a binder, while aggregates provide strength and durability to the concrete structure. You can find concrete in a variety of applications, including buildings, bridges, highways, and dams, due to its versatile nature.
Different types of concrete have varying compositions, which result in different strengths and mechanical properties. One of the key parameters used to describe the mechanical behavior of concrete is the modulus of elasticity.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
In general, the modulus of elasticity is a material property that describes the stiffness or how resistant a material is to deformation when subjected to an applied load. Mathematically, it represents the ratio between the stress and strain in a material, as shown in the following equation:
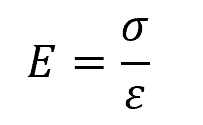
Where:
- E = modulus of elasticity [Pa or psi]
- σ = applied stress [Pa or psi]
- ε = corresponding strain [unitless]
Stress is the force applied per unit area, while strain is a dimensionless quantity that refers to the change in length divided by the original length of the material.
The modulus of elasticity is often associated with tensile properties of materials. However, when it comes to concrete, the situation is a bit more complex. Concrete is a composite material that exhibits different elastic properties depending on whether it is subjected to tensile or compressive loads.
Concrete is relatively weak in tension, and its tensile strength is much lower than its compressive strength. When concrete is subjected to tensile forces, it tends to crack and deform. On the other hand, when subjected to compressive forces, concrete has a higher resistance to deformation.
For structural design and analysis, its modulus of elasticity in compression is generally used because concrete members, such as columns and beams, primarily experience compressive forces in most building and infrastructure applications.
Below is a sample stress-strain curve of concrete loaded in compression.
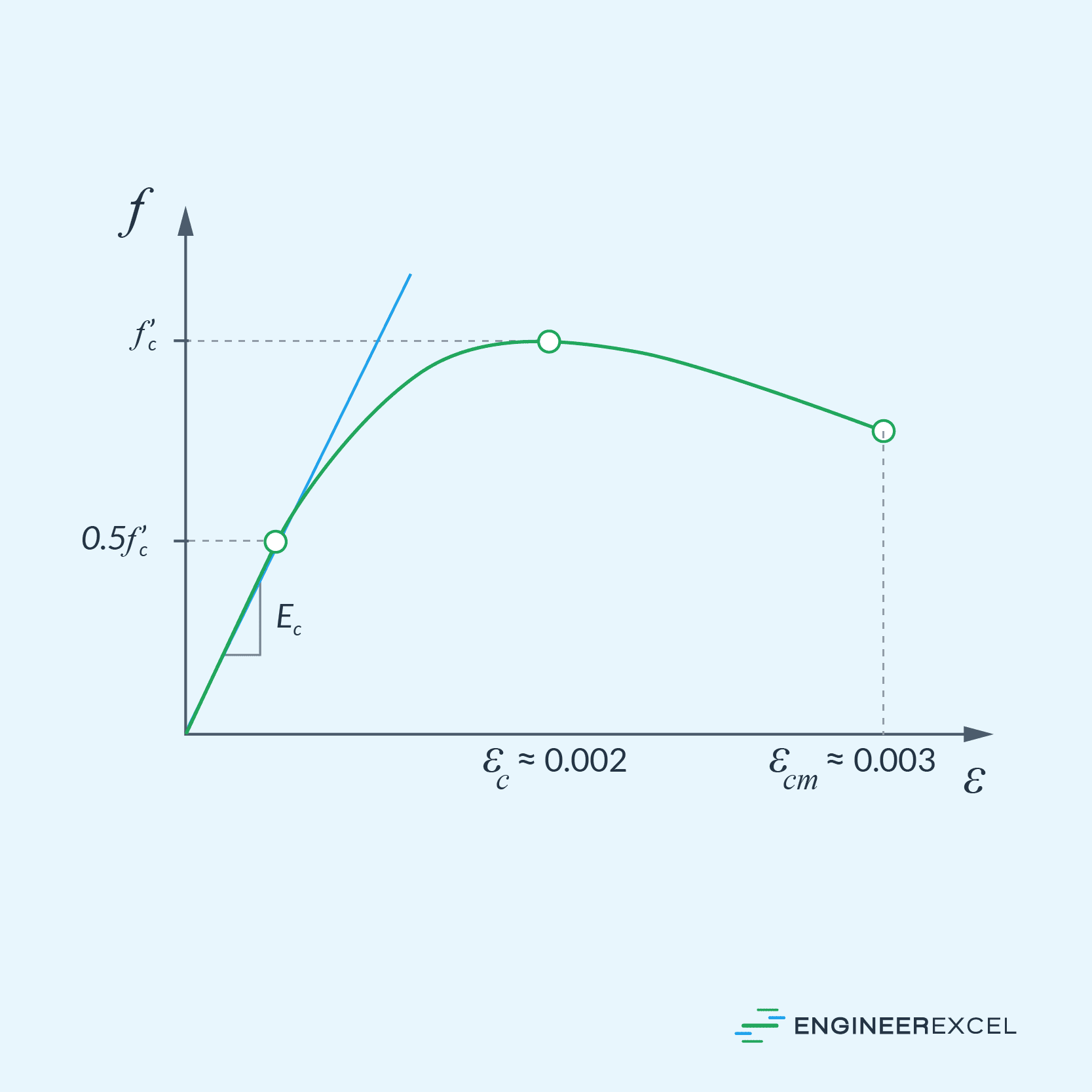
In the diagram above, Ec is the compressive modulus of elasticity and fc’ is the compressive strength of the concrete.
Factors Influencing Modulus of Elasticity of Concrete
The modulus of elasticity of concrete depends on various factors, such as composition, strength, and aggregate properties.
Concrete Composition
The components used in making the concrete, such as cement, sand, water, and aggregates, have a significant effect on its elasticity. For instance, increasing the cement content results in a higher modulus of elasticity, while the use of fly ash or slag cement may reduce it.
Concrete Strength
One of the most influential factors is the compressive strength of the concrete. As the strength increases, so does the modulus of elasticity. High-strength concrete typically has a higher modulus of elasticity compared to low-strength concrete.
Aggregate Properties
The type, size, and proportions of the aggregates you use in your concrete mix also impact the modulus of elasticity. For example, the use of lightweight aggregates leads to a lower modulus of elasticity, while the use of denser aggregates, like crushed stones, results in a higher modulus.
Age of the Concrete
The modulus of elasticity of concrete evolves over time. As the concrete hardens and gains strength, its modulus of elasticity increases. Be aware that the rate of increase will slow down once the majority of the hydration process has occurred, usually after 28 days.
Curing Conditions
The conditions under which the concrete cures play a role in determining its modulus of elasticity. Proper curing, such as maintaining adequate temperature and humidity levels, allows the concrete to develop its optimal elastic properties.
Calculating Modulus of Elasticity of Concrete
The modulus of elasticity of concrete can be calculated using empirical equations derived from experimental data. Alternatively, it can be determined through laboratory testing.
The most commonly used empirical equation is the one proposed by the American Concrete Institute (ACI). According to ACI’s Structural Concrete Building Code, the modulus of elasticity for concretes with densities ranging from 1440 to 2560 kg/m3 shall be permitted to be taken as:
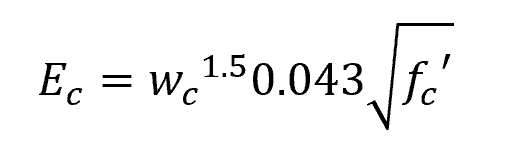
Where:
- Ec = compressive modulus of elasticity of concrete [MPa]
- wc = density of concrete [kg/m3]
- fc’ = compressive strength [Mpa]
For normal weight concrete, it shall be permitted to be taken as:
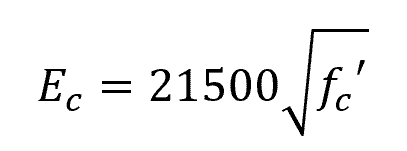
Note that these empirical equations are dimensionally non-uniform, hence, it is important to always use the correct units of measurement when using them. In English units, the formula becomes:
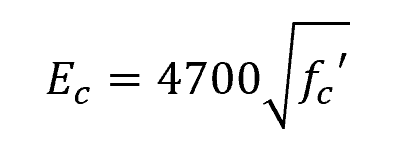
Where:
- Ec = compressive modulus of elasticity of concrete [psi]
- fc’ = compressive strength [psi]
While ACI’s empirical equation offers a quick estimate, it’s essential to consider other factors that influence the modulus of elasticity, such as the aggregate type, curing process, and loading rate. Laboratory testing, including the Static Modulus of Elasticity Test (ASTM C469) or the Dynamic Modulus of Elasticity Test (ASTM C215), can provide more accurate results for your specific concrete mix.
Measuring Modulus of Elasticity of Concrete
To determine the compressive strength and modulus of elasticity of concrete, standard cylinder tests are typically conducted in accordance with ASTM C 39. These tests involve testing concrete cylinder samples with standard dimensions of 150 mm in diameter and 300 mm in height, which are cured for at least 28 days in a controlled environment to ensure consistency.

A compression test is conducted on these samples using a universal testing machine, typically loaded at a constant rate. Throughout the test, the applied load and axial deformation are recorded and graphed. The initial linear portion of the resulting curve represents the elastic behavior of the concrete, from which the modulus of elasticity is obtained by dividing the stress by the corresponding strain within this linear region.
It’s important to note that variations in concrete mix design, curing conditions, and testing methods can lead to differences in measured modulus values. Therefore, it’s crucial to control these factors as much as possible and compare results with established empirical relationships and guidelines to validate findings.
Applications of Modulus of Elasticity of Concrete
The modulus of elasticity of concrete is a crucial property used to calculate the deformation of structures under load, predict stress distribution, and determine load capacity. It plays a vital role in designing reinforced concrete structures and understanding the response of concrete to various loads.
In structural design, engineers use the modulus of elasticity of concrete to analyze structural elements such as beams, columns, and slabs to ensure adequate load-bearing capacity and stability. It is used to calculate deflections of concrete elements subjected to applied loads, accounting for serviceability limit states that maintain the functionality and durability of structures.
In prestressed concrete design, the modulus of elasticity is needed to evaluate the stress in the prestressing tendons. Moreover, it plays a crucial role in seismic design, where maintaining sufficient stiffness is essential in preventing excessive deformations under seismic loads.
Lastly, evaluating thermal effects on concrete structures requires the modulus of elasticity. You use it to estimate the stress induced due to temperature variations, which can significantly impact long-term structural performance. Addressing these effects is crucial for the longevity and serviceability of your concrete structures.
