The Mohr-Coulomb criterion is one of many theories used to predict failure of brittle materials. It is a mathematical model describing the conditions under which a brittle material will fail under stress, incorporating cohesion and internal friction angle as key parameters.
Understanding the Mohr-Coulomb Failure Criterion
Brittle materials, like gray cast iron, fail abruptly through fracture without any noticeable yielding. In brittle materials with similar behavior under tension and compression, failure happens when the maximum tensile stress in the material reaches the ultimate normal stress it can withstand under simple tension.

However, for some brittle materials, the properties under tension and compression are not the same. In these cases, the Mohr-Coulomb failure criterion, based on the use of Mohr’s circle, can be used to predict failure.
The Mohr-Coulomb failure criterion is a widely used method to determine the failure of brittle materials such as rocks, soils, and concrete under varying stress conditions. Named after Charles-Augustin de Coulomb, who introduced the concept, and Christian Otto Mohr, who developed a generalized form of the theory, this failure criterion is based on the concept of shear strength, which relates the shear stress and normal stress acting on a material.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
The Mohr Coulomb failure criterion is represented by the equation:
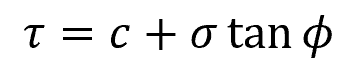
Where:
- τ = shear stress on failure plane [Pa]
- c = cohesion of the material [Pa]
- σ = normal stress on plane [Pa]
- φ = angle of internal friction [rad]
The cohesion (c) refers to the inherent strength of the material that holds it together, while the angle of internal friction (φ) represents the material’s resistance to sliding or shearing.
Note that this formula assumes compression to be positive. This is because this theory applies to materials that are typically subjected to compression, for which the compressive strength far exceeds the tensile strength.
In a Mohr diagram, the above formula is represented by a straight line inclined to the σ-axis by the angle φ, as shown in the diagram below. Failure occurs when the diamater of Mohr’s circle, represented by the circle of diameter (σI – σIII), becomes tangent to or goes outside of the failure envelope.
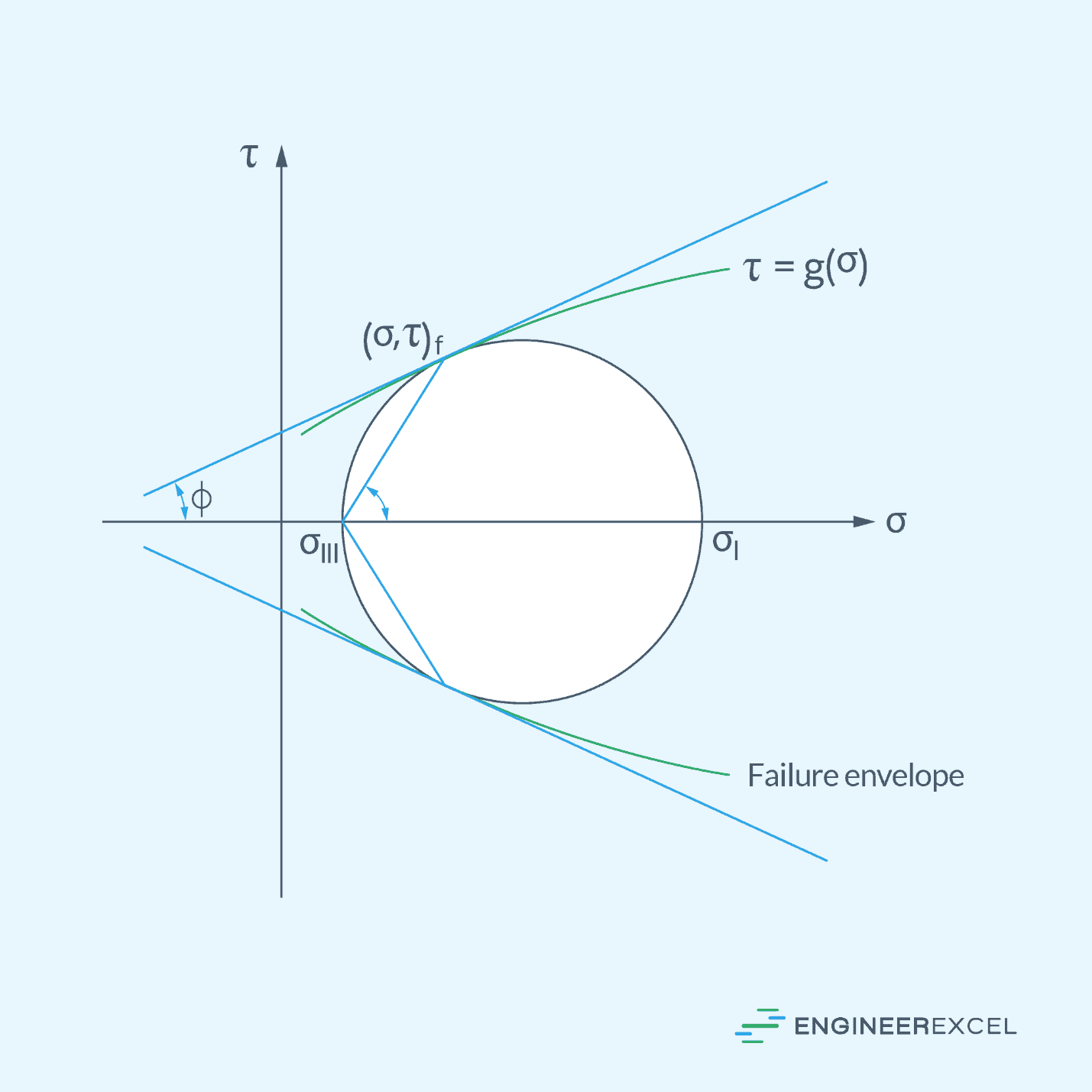
Mohr-Coulomb Failure Criterion in Terms of Principal Stresses
By constructing a Mohr circle tangent to the lines and using trigonometric relations, the alternative form of the Mohr Coulomb failure criterion, in terms of principal stresses, can be expressed as follows:

Where:
- σI = minor principal stress [Pa]
- σIII = major principal stress [Pa]
The Mohr-Coulomb criterion, as depicted in the equation above, assumes that failure is not affected by the value of the intermediate principal stress. However, in reality, the failure of brittle materials usually has some slight dependence on the intermediate principal stress. Nevertheless, the Mohr-Coulomb model is widely accepted as sufficiently accurate for most practical purposes.
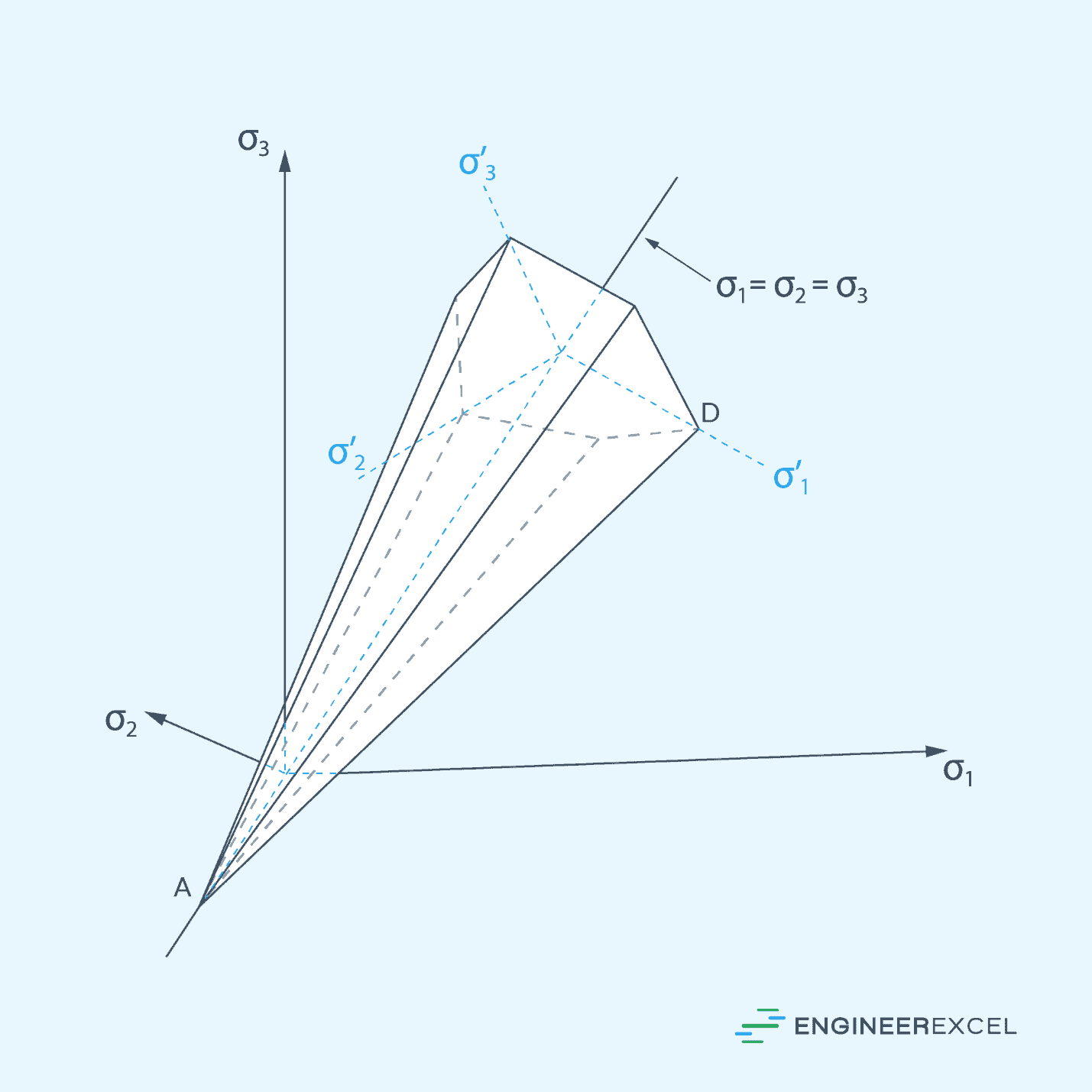
Mohr-Coulomb Criterion in Three Dimensions
In three dimensions, the Mohr-Coulomb criterion can be expressed as follows:
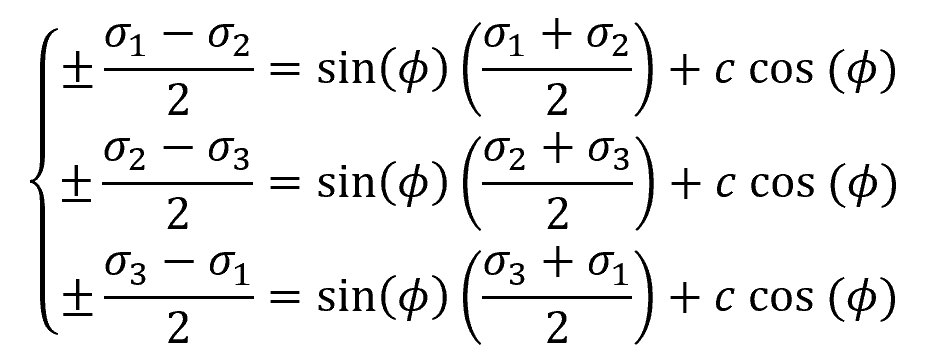
Where:
- σ1, σ2, σ3 = principal stresses [Pa]
These equations form a failure surface composed of six planes that intersect one another along six edges, defining a hexagonal pyramid. This is shown in the diagram below.
Applications of Mohr-Coulomb Failure Criterion
The Mohr-Coulomb criterion is used to explain how brittle materials like concrete and rubble piles respond to shear stress and normal stress. It has several advantages, including its mathematical simplicity, clear physical meaning of material parameters, and widespread acceptance.
This criterion generally applies to classical engineering materials where the compressive strength is much higher than the tensile strength, and is relevant to at least part of their shear failure envelope. In the field of soil mechanics and geotechnical engineering, it is used to predict the failure of soils and rocks under various stress conditions. It is particularly applicable in situations where soils experience both normal and shear stresses, such as in slopes, foundations, and retaining walls.
Experiments have shown that the criterion applies well to rock when all principal stresses are compressive, with the uniaxial compressive strength being much greater than the uniaxial tensile strength. However, some modification is necessary when tensile stresses are present, as the theoretical uniaxial tensile strength predicted from Mohr-Coulomb does not align with experimental measurements.
