The section modulus of a structural member is a specific geometric property that is calculated based on the shape of the member and its cross-section. The section modulus is used to directly calculate the strength of a structural member under a compressive or tensile force. The larger the section modulus, the stronger the member is, meaning it will be able to support larger forces without permanent damage or failure.
When calculating the section modulus, the formulas determine the bending work that is being done by the material fibers at the extremes, i.e., the top and bottom, of the member. A common shape used in structural engineering is a square tube, which is a specialized case of a hollow rectangular cross-section. There are two types of section modulus, elastic and plastic.
Elastic Section Modulus of Square Tube
The elastic section modulus is used for engineering applications that are within the elastic limit, and is applicable up to the yield point of most metals and other common materials used in structural design. The general form of the calculation for the elastic section modulus S is:
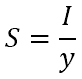
where I is the area moment of inertia of the tube and y is the distance from the neutral axis of the tube to any point in the material.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.

Specifically, for a square tube, the elastic section modulus is calculated as follows:
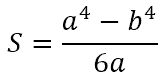
where a is the external dimension and b is the internal dimension, both with SI units of m. The following figure provides an example of these, with the neutral axis marked by the dashed line:
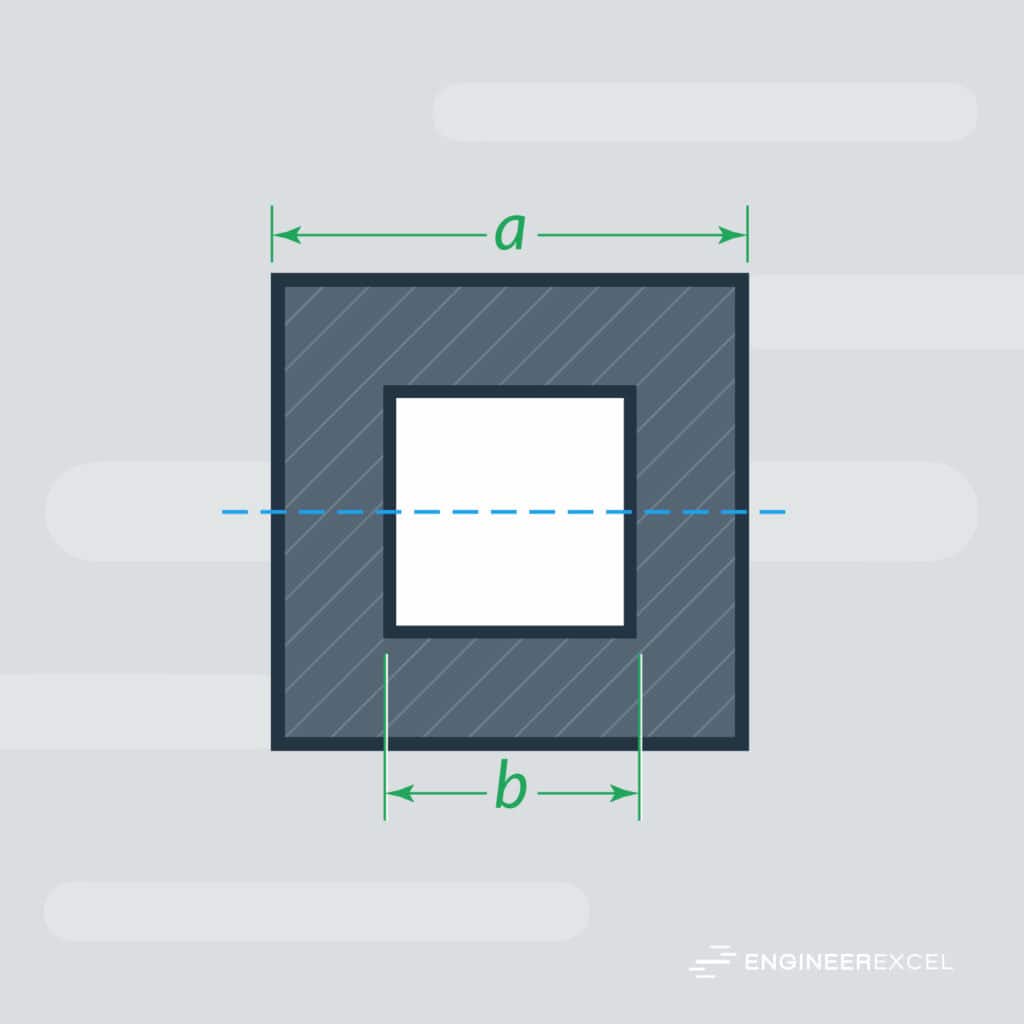
Square Tube Section Modulus Calculator
Section Modulus of Common Square Tube Profiles
Plastic Section Modulus of Square Tube
For materials where elastic yielding can be accepted and plastic deformation is within an acceptable limit, the plastic section modulus is used. In these engineering situations, the objective is to stay below the plastic limit to prevent any permanent plastic deformation.

When calculating the plastic section modulus, it is necessary to know where the plastic neutral axis (PNA) is located. The PNA defines the separation between the portion in compression and the portion in tension. In the case of a square tube, the PNA is the same as the neutral axis because the section is constant about both.

The general form of the plastic section modulus Z is:
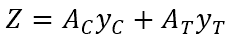
where AC and AT are the cross-sectional areas on either side of the PNA and yC and yT are the distances from the PNA to each cross-sectional centroid.

In the specific case of a square tube, the plastic section modulus is calculated as follows:
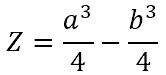
The plastic section modulus can be used to calculate the plastic moment Mp, which may be referred to as the full capacity of the cross-section. The yield strength of the material Fy relates the two as follows:
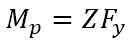
Application Of the Section Modulus
The elastic section modulus is related to the plastic section modulus by a shape factor k as follows:

The shape factor is useful in determining the structural capacity of the member beyond the material elastic limit.

Because the compression of a structural member is generally the more critical case, the calculation of the section modulus with regard to compression is often used as the limiting case of a structural design. Therefore, when calculating a conservative design, the highest compressive load and lowest elastic section modulus of a section are used together. Alternatively, the highest load, either compressive or tensile, may be used for a more detailed design.
