Fluid flow can be categorized into different flow regimes based on how the fluid particles behave under various conditions. In fluid dynamics, there are three flow regimes: laminar flow, turbulent flow, and transitional flow, each characterized by distinct patterns of fluid motion and behavior.

In this article, we present an in-depth analysis of the characteristics of laminar flow.
What is Laminar Flow
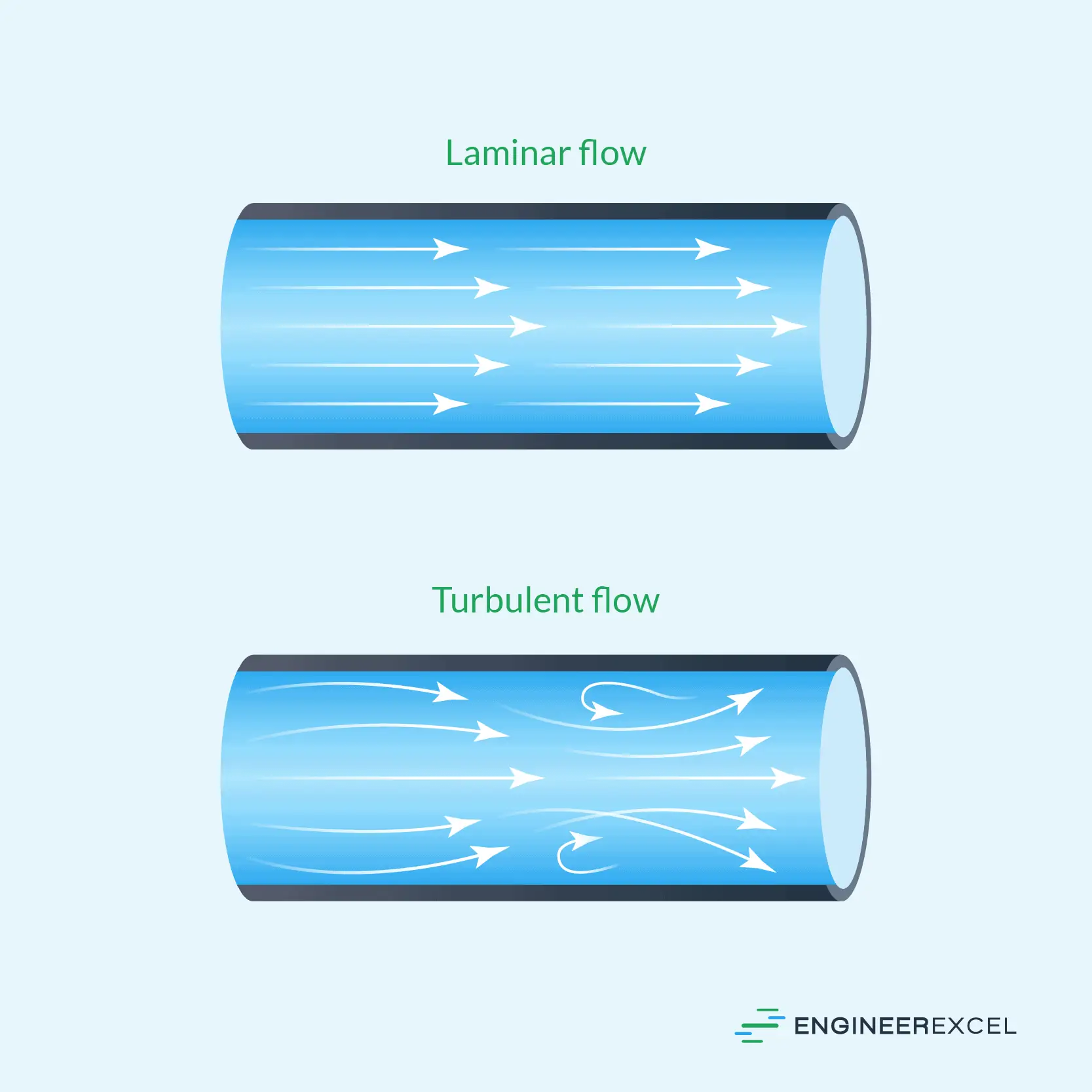
Laminar flow is a type of fluid flow where fluid particles move in smooth, parallel layers, sliding past one another with minimal interaction. In this flow regime, the fluid travels in a highly ordered manner, with minimal mixing or disruption. It typically occurs at lower velocities and in situations with a low degree of roughness or turbulence.
The primary difference between laminar flow and turbulent flow is the nature of the fluid motion. In turbulent flow, fluid particles move in a highly disordered and chaotic manner, with rapid fluctuations in pressure and velocity. This creates unpredictable and erratic flow patterns, in contrast to the smooth, ordered motion of laminar flow.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
One critical parameter for determining the flow type is the Reynolds number, which relates the inertial forces to the viscous forces in a fluid, as shown in the following equation:
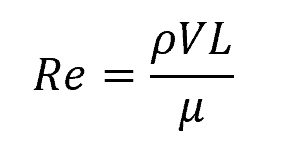
Where:
- Re = Reynolds number [unitless]
- ρ = density of the fluid [kg/m3]
- V = velocity of the fluid [m/s]
- L = characteristic length of the flow [m]
- μ = dynamic viscosity of the fluid [Pa-s]
Reynolds number provides a way to predict and analyze the transition between laminar and turbulent regimes in various fluid systems. In general, a low Reynolds number is indicative of laminar flow, while higher values point to turbulent flow. However, the critical value at which the transition starts depends on various factors, such as the geometry of the conduit, fluid properties, and surface roughness.
In smooth circular pipe flow, for example, the flow is generally considered laminar at Reynolds numbers below 2300. Beyond this critical value, the flow starts to transition into the turbulent flow regime.
The table below summarizes the critical Reynolds numbers for laminar flow in different geometries.
Characteristics of Laminar Flow
Low Velocity
In laminar flow, the fluid moves at a relatively low velocity, which helps maintain a smooth, orderly motion. As a result, you won’t find turbulence or chaotic movement in this type of flow. It’s crucial for applications where stability is needed, such as in lab experiments and precision fluid management.
Layered and Streamlined Flow
In laminar flow, the fluid moves in coordinated layers, with each layer sliding smoothly over the one below it. This creates a clear distinction between the layers, reducing the opportunity for turbulent mixing between them.

The flow pattern in laminar flow is defined by streamlines, which are elongated, parallel, and evenly spaced lines that represent the fluid’s path. As you observe these streamlines, you’ll find they don’t intersect or overlap, indicating a highly organized flow pattern.
Well-Defined Velocity Distribution
Because adjacent fluid layers tend to slide smoothly past one another, with no rapid fluctuations, you’ll notice a well-defined velocity distribution across the flow profile of a laminar flow. This characteristic allows for predictable and controllable fluid behavior. However, the shape of the velocity profile generally depends on the specific geometry of the flow.
In circular pipe flow, for example, the velocity profile tends to be parabolic. According to Poiseuille’s Law, the velocity of fluid in a laminar pipe flow can be mathematically expressed as a function of radius as follows:
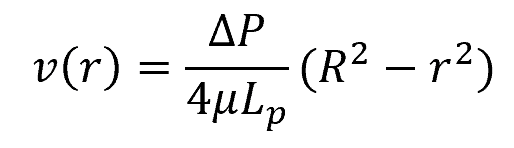
Where:
- v(r) = velocity of the fluid at a radial distance r from the center of the pipe [m/s]
- ΔP = pressure difference between the two ends of the pipe [Pa]
- μ = dynamic viscosity of the fluid [Pa-s]
- Lp = length of the pipe [m]
- R = radius of the pipe [m]
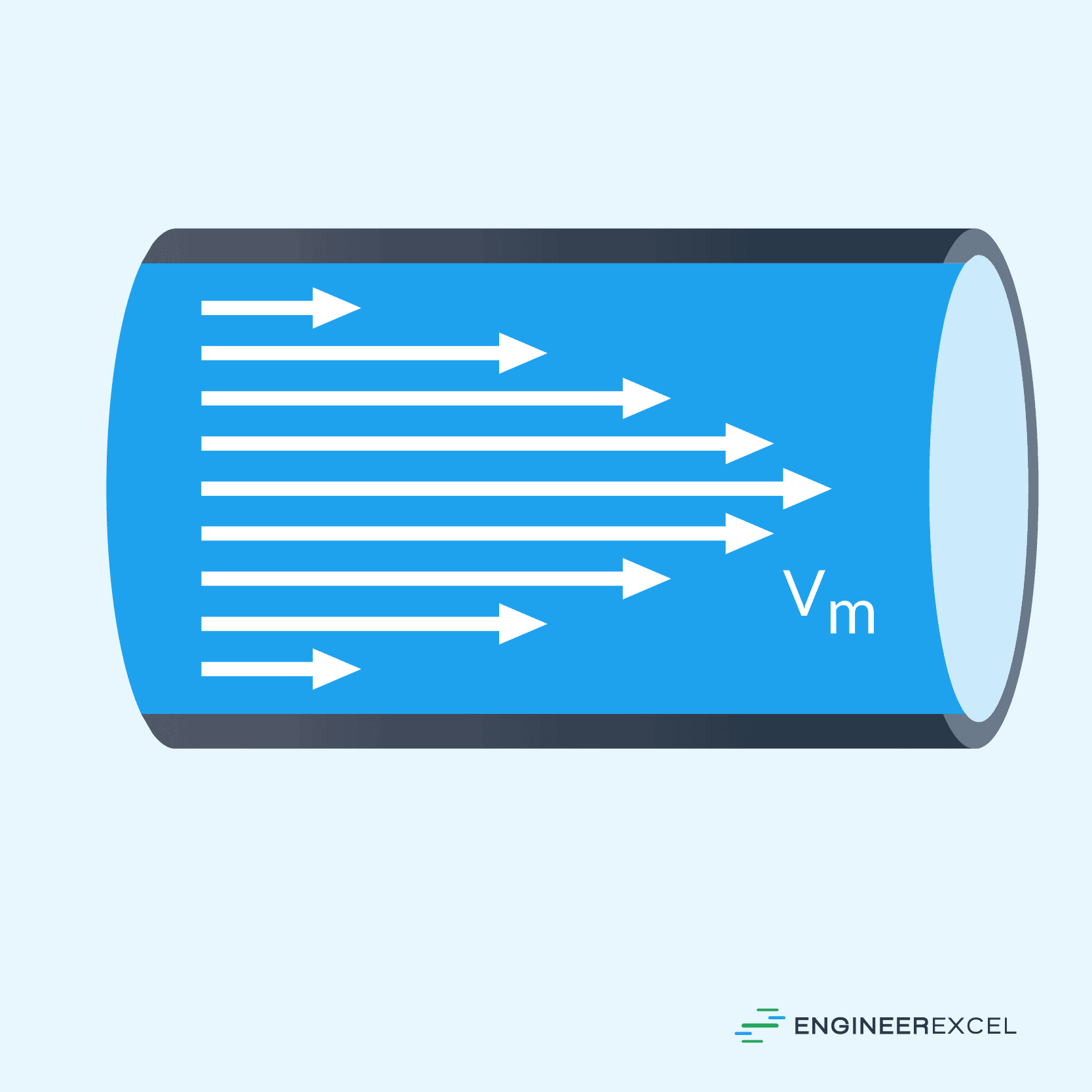
In this equation, the velocity is highest at the center of the pipe and decreases linearly with increasing radial distance from the center. This results in a parabolic velocity distribution, as shown in the diagram below. This velocity profile is valid for incompressible, Newtonian fluids in steady-state laminar flow.
Minimal Friction Loss
Another key characteristic of laminar flow is its minimal friction loss. Since the layers slide smoothly over each other and the flow is well-organized, there is less resistance and energy lost to friction. This allows you to conserve energy and resources, making laminar flow an efficient system in various applications.
Factors Influencing Laminar Flow
There are several factors that affect the behavior of laminar flow. These include factors such as fluid viscosity, flow velocity, surface roughness, and pipe diameter.
Viscosity
The viscosity of a fluid plays a crucial role in determining the flow behavior. A higher viscosity leads to a more laminar flow, as the fluid layers resist rapid motion and remain orderly. On the other hand, low-viscosity fluids tend to have a higher chance of developing turbulence due to their ability to move quickly and mix easily.
Flow Velocity
The flow velocity has a direct impact on laminar flow conditions. When you increase the velocity of a fluid in a pipe, the fluid particles move faster, increasing the chance of encountering disturbances. Conversely, a slower velocity makes it easier for the fluid to maintain a laminar flow pattern, as there is less energy available to disturb the flowing layers.
Surface Roughness
Surface roughness affects laminar flow by increasing friction and disrupting the smooth flow of a fluid, leading to a higher pressure drop, early flow separation, and the potential for a transition to turbulent flow at lower Reynolds numbers. These effects can reduce the efficiency of fluid systems, increase energy losses, and impact heat transfer characteristics due to changes in the boundary layer’s behavior.

