Laminar flow is a smooth, orderly flow of a fluid in which it moves in parallel layers with minimal mixing or turbulence. In laminar flow, the fluid velocity at any given point remains relatively constant over time, and the flow pattern is characterized by well-defined streamlines. In this article, we discuss the fundamentals of laminar flow, including the importance of Reynolds number, factors affecting laminar flow, applications of laminar flow, and laminar flow control techniques.
Defining Laminar Flow
Laminar flow refers to fluid flow in which fluid particles move in smooth, parallel layers along the flow direction. This type of flow occurs when fluid motion is coordinated and ordered, as shown in the illustration below.
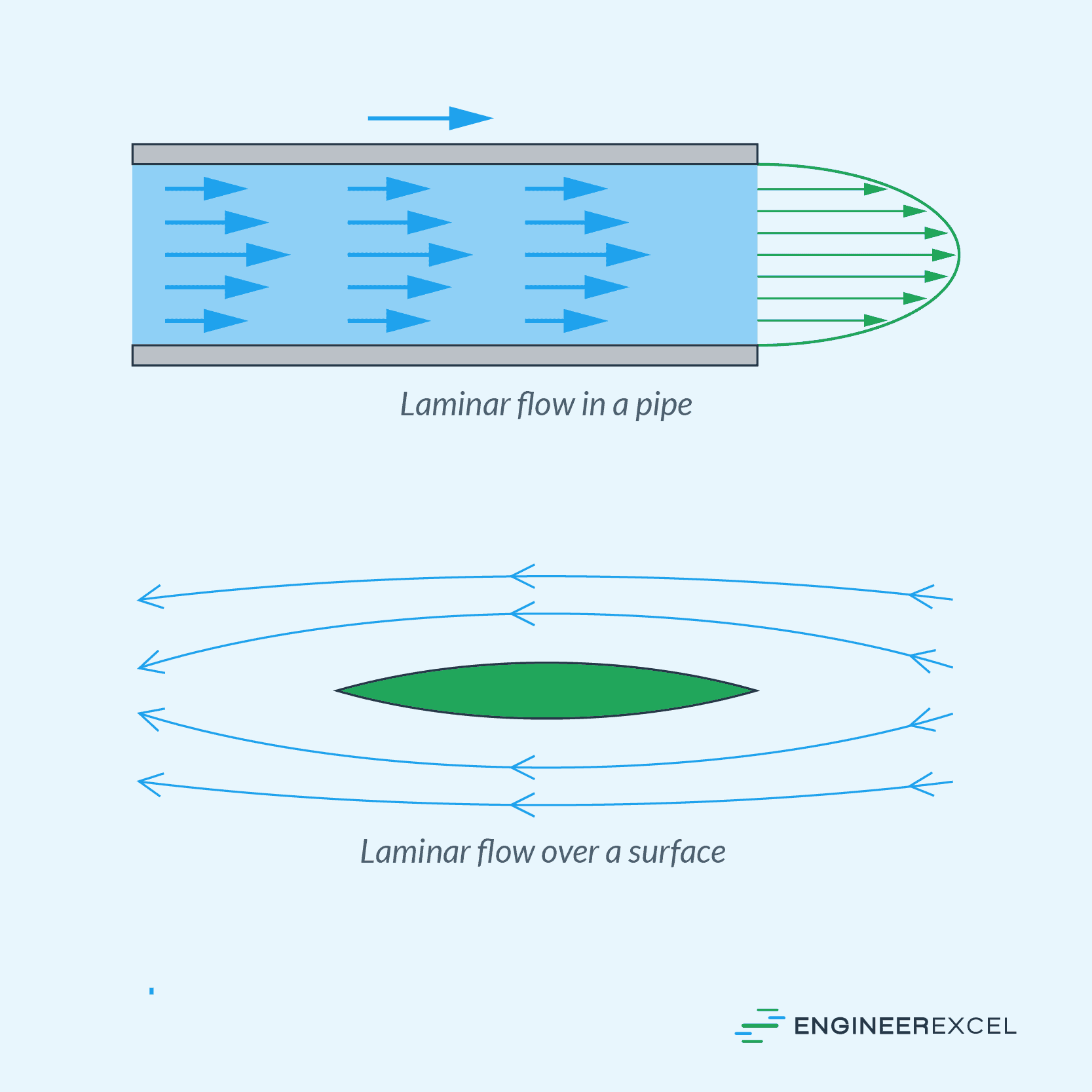
In laminar flow, fluid particles follow a steady, continuous path, and there’s little to no mixing between the layers. This is a result of the dominant role of fluid viscosity and the balance of forces. Viscous forces, which resist the relative motion between fluid layers, dominate inertial forces that are induced by the acceleration of fluid particles.
In general, laminar flow requires less energy to maintain than turbulent flow, as it experiences lower fluid friction losses. Due to its ordered nature, laminar flow is also easier to model and predict than turbulent flow, which has a chaotic and complex nature.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.

However, it’s important to note that laminar flow is not always the preferred state in practical applications. In some cases, such as heat exchangers, turbulent flow can have desirable properties like enhanced mixing or increased heat transfer rates. However, understanding and controlling laminar flow is crucial in various engineering fields, including microfluidics, lubrication, and drag reduction.
Reynolds Number for Laminar Flow
The tendency of a fluid flow to be laminar or turbulent can be quantified using the Reynolds number (Re). This dimensionless number is the ratio of inertial forces to viscous forces in a fluid flow and can be calculated as:
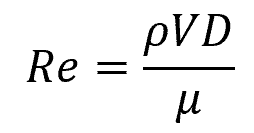
Where:
- ρ = fluid density [kg/m3]
- V = flow velocity [m/s]
- D = characteristic length scale [m]
- μ = fluid dynamic viscosity [Pa-s]
The characteristic length depends on the geometry of the flow. In a pipe, for example, this can be the hydraulic diameter.
When the Reynolds number is below a critical value, the flow is predominantly laminar. As the Reynolds number increases, the flow can transition to turbulent if disturbances in the flow overwhelm the stabilizing effects of viscosity.
The critical Reynolds number at which a flow remains laminar is not a universal constant. It varies depending on the shape of the object or conduit through which the fluid is flowing, the surface roughness of that object, and other environmental conditions.

For example, in a smooth, straight pipe, the critical Reynolds number is typically around 2,300. However, in a pipe with irregularities or obstacles, the transition to turbulence might occur at a lower Reynolds number. Conversely, in very smooth and streamlined geometries, the flow might remain laminar at higher Reynolds numbers.
Factors Affecting Laminar Flow
Fluid Properties
The properties of the fluid play a significant role in determining the laminar flow behavior, particularly viscosity and density.
Viscosity refers to the resistance of a fluid to deformation. A higher viscosity fluid is more likely to maintain a laminar flow, as it resists the formation of turbulence. For example, a highly viscous fluid, like honey, will exhibit a more laminar flow than a less viscous fluid, like water.
Density, which is the mass per unit volume of a fluid, also influences the laminar behavior of the flow. In general, fluids with higher densities result to higher momentum, which makes it easier to overcome the effect of viscosity.
Velocity of Flow
Another critical factor affecting laminar flow is the velocity of the fluid. As the flow velocity increases, the value of the Reynolds number increases, thereby increasing the potential for turbulence.
The velocity profile of laminar flow in a pipe is parabolic in nature, with zero velocity at the pipe walls and maximum velocity at the center.
Surface Roughness
The surface roughness of the conduit or pipe through which the fluid is flowing can also impact the laminar flow. Rough surfaces can induce turbulence by disrupting the smooth flow of fluid layers close to the wall. In general, smoother surfaces promote laminar flow, whereas rougher surfaces can lead to turbulent flow.
Flow Geometry
The shape and complexity of the flow geometry have a substantial impact on the Reynolds number. In a simple, streamlined flow geometry, such as a straight pipe or a smooth channel, the flow tends to be more predictable and is often laminar at lower Reynolds numbers. However, as the flow geometry becomes more complex with irregularities, obstacles, or abrupt changes in shape, the Reynolds number tends to increase, favoring turbulent flow. For example, flow separation, sharp corners, and obstructions can disrupt the flow, causing it to transition to turbulence at lower Reynolds numbers.

The characteristic length plays a fundamental role in determining the Reynolds number. It is a reference length associated with the geometry of interest. For different flow scenarios, the choice of characteristic length can vary. In a pipe, the characteristic length is typically the pipe diameter, whereas in a flow past a cylinder, it might be the cylinder’s diameter or radius. Increasing the characteristic length directly contributes to higher Reynolds numbers, as the scale of the flow field increases. This higher Reynolds number indicates a greater influence of inertial forces compared to viscous forces, favoring the onset of turbulence. Conversely, reducing the characteristic length decreases the Reynolds number, promoting the prevalence of laminar flow by emphasizing viscous effects.
Applications of Laminar Flow
Understanding laminar flow is essential in various engineering applications.
In aerospace engineering, for example, laminar flow over the surfaces of aircraft wings is desirable because it reduces drag and enhances the overall aerodynamic efficiency of the aircraft. In fluid distribution systems, maintaining laminar flow inside conduits can be advantageous for applications that require a more precise control of flow rate and lower pressure losses.
In biomedical engineering, laminar flow is utilized in areas like microfluidics and flow cytometry. In microfluidics, precise control of laminar flow enables researchers to develop devices for drug delivery, diagnostics, and tissue engineering. In flow cytometry, laminar flow behavior allows for accurate analysis of individual cells suspended in a fluid stream.
Laminar Flow Control Techniques
Laminar flow control is essential in reducing drag and improving the efficiency of fluid flow systems. There are two primary techniques for controlling laminar flow: active control and passive control.
Active Control
Active control techniques involve the use of external devices or energy to manipulate the fluid flow. Some common active control methods include:
- Suction: Removing a small amount of fluid near the wall to suppress turbulence and maintain a laminar flow. This is often done using numerous tiny holes or porous materials embedded in the surface.
- Blowing: Opposite to suction, blowing involves injecting a small amount of fluid near the wall. This method can help stabilize the boundary layer and delay the onset of turbulence.
- Vibration: Applying oscillatory motion to the structure or part of it to control the boundary layer, which may help maintain a laminar flow.
- Electromagnetic manipulation: Utilizing electric and magnetic fields to affect the fluid flow, primarily when the fluid is electrically conductive, such as in magnetohydrodynamics.
These methods often require additional energy input and can be complex to implement. However, they may provide significant advantages in specific applications, such as reducing skin friction drag on aircraft wings or enhancing mixing in industrial processes.
Passive Control
Passive control focuses on the use of geometric modifications and surface treatments to influence the flow naturally, without the need for external devices or energy input. Some common passive control methods include:
- Surface roughness: Manipulating the surface roughness can help in maintaining laminar flow by causing the transition to turbulence to occur at higher Reynolds numbers.
- Riblets: Small, longitudinal grooves on the surface that can help decrease skin friction drag by reducing the effective eddy size in the boundary layer.
- Streamwise vortex generators: These are small, low-profile devices mounted on the surface that can induce streamwise vortices, delaying separation and turbulent transition.
- Laminar-flow wings or airfoils: These are wings or airfoils specifically designed to maintain laminar flow over a considerable portion of their surface, by using tailored geometries, such as a favorable pressure gradient to enhance the stability of the boundary layer.
Passive control techniques are generally less complex and more energy-efficient than active control methods. However, their effectiveness depends on the application, and they may not be sufficient in all cases.
