The average shear stress is the force per unit area acting parallel to a material’s surface. It occurs when two parts of a material slide or move relative to each other in opposing directions along a plane. In this article, we will discuss the concept of average shear stress, its formula, and how it can be used in practical engineering applications.
Average Shear Stress
In a structure, shear stress is the force per unit area that arises when a force is applied parallel to the surface of a material. It occurs when two parts of a material slide or move relative to each other in opposing directions along a plane, as shown in the diagram below.
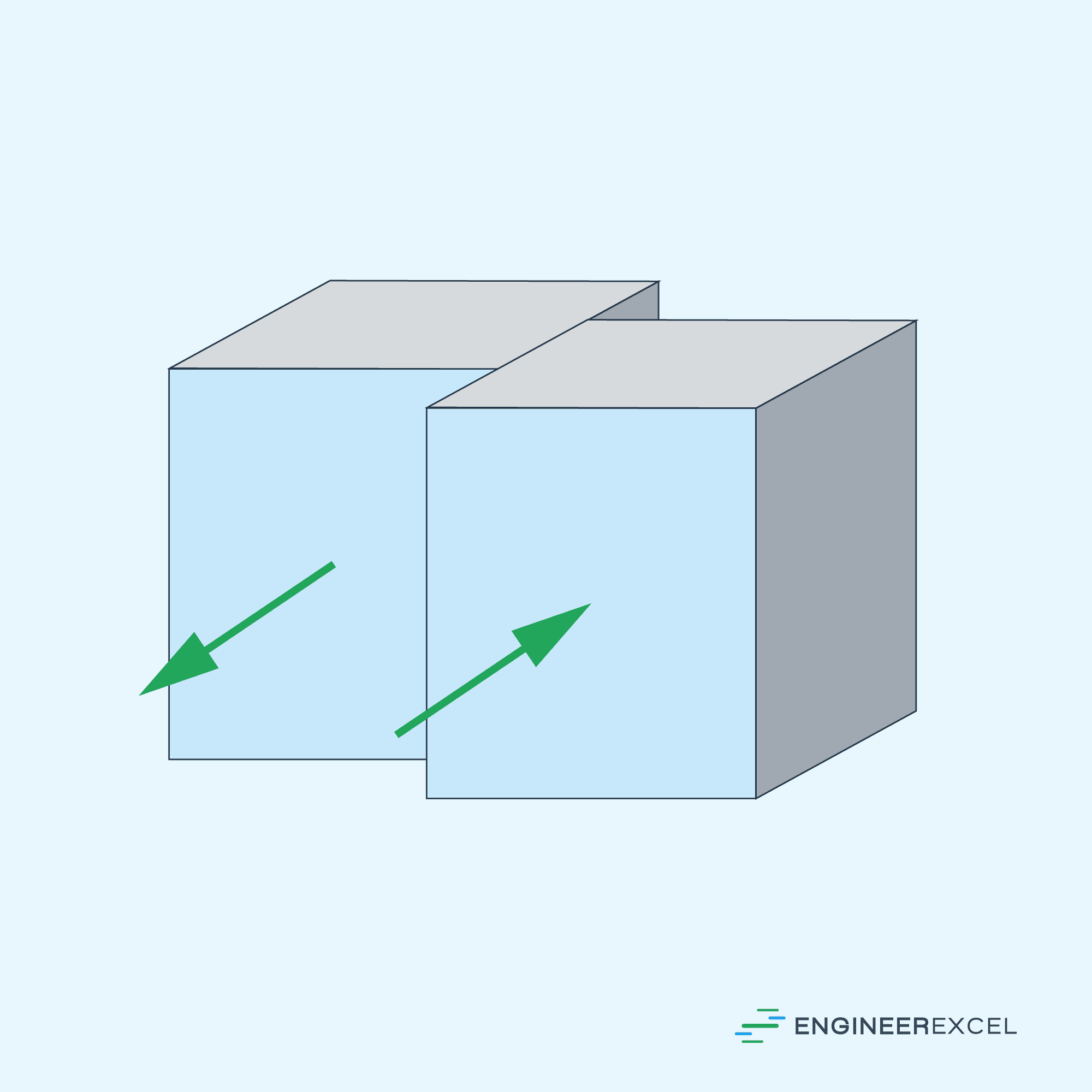
The distribution of shear stress within a material or across a structural component is not always uniform and can vary due to several factors, including loading type, component geometry, and material properties.
For instance, in a simple beam under a transverse load, the maximum shear stress occurs at the neutral axis, where bending stress is zero, and decreases linearly towards the top and bottom surfaces of the beam, following a parabolic distribution. Therefore, using the average shear stress may not always provide an accurate representation of the actual shear stress distribution within the material, and actual shear stresses can be much higher in some parts of the material.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
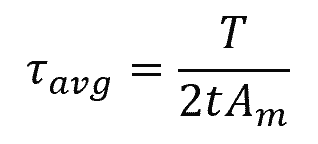
However, despite the potential inaccuracies in predicting shear stress, engineering practice often relies on the concept of average shear stress. Average shear stress is a simplified representation of the shear forces acting on a material, considering the entire section as a whole. While there may be variations in shear stress within a material, using the average value simplifies calculations and can still provide a reliable and safe design.
Examples of where average shear stress is commonly used in engineering include determining design sizes for fasteners like bolts and calculating the bonding strength of glued joints under shear loads. Engineering codes and standards often permit the use of average shear stress in such cases because it simplifies design procedures without compromising safety.
The concept of average shear stress helps to examine the overall impact of shear forces on a material, rather than focusing on an infinitesimally small point. Another application of average shear stress calculations is in determining the shear modulus of a material.

The shear modulus, typically represented by the letter G, is a measure of a material’s ability to resist shear deformation under a given applied force. It can be calculated from the material’s elastic modulus and Poisson’s ratio, which are fundamental properties that describe the material’s behavior under stress. Knowing the shear modulus is essential for designing reliable and durable materials and structures.
Average Shear Stress Formula
The average shear stress distributed over an area can be calculated using the following formula:
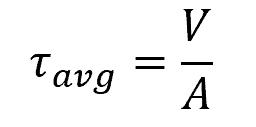
Where:
- τavg = average shear stress [Pa]
- V = internal resultant shear force at the section [N]
- A = area at the section [m2]
In this context, the internal resultant shear force acts parallel to the area on which it is applied, as shown in the diagram below. The average shear stress is the same at each point located on the section, and it acts in the same direction as the internal shear force.

The average shear stress formula is based on several assumptions that might not always hold true in real-life situations. One such assumption is that the material is homogeneous and isotropic, meaning that its properties remain constant throughout the entire volume and do not change with the direction. This assumption might not be accurate for materials with varying composition or those exhibiting anisotropic behavior.
Another assumption is that the deformation is small and linearly elastic, implying that the material always returns to its original shape and size once the load is removed. In reality, materials can exhibit nonlinear behavior, and sometimes deformations can be large enough to cause changes in the material properties. Moreover, the average shear stress formula often disregards the effects of temperature, fatigue, and other environmental factors.
Example Problem
Problem: A pin with a circular cross-section of radius R = 5 cm is subjected to a transverse force of F = 5000 N. If the pin is supported by two fixed leaves, calculate the average shear stress in the pin.
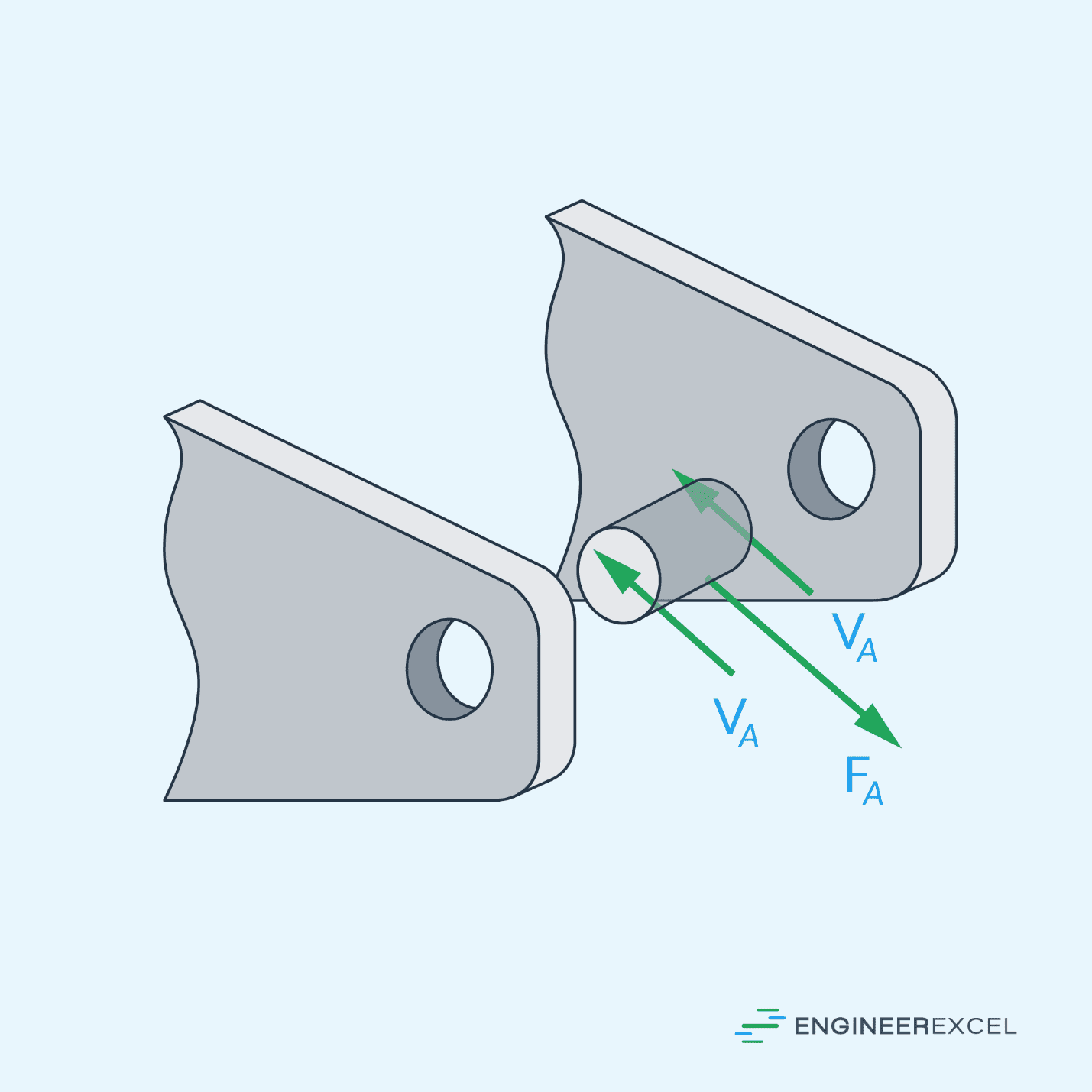
Solution:
This case is called double shear. To get the internal resultant shear force, we simply divide the load by 2:
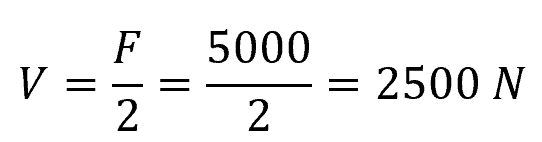
The area of the cross-section of the pin is:
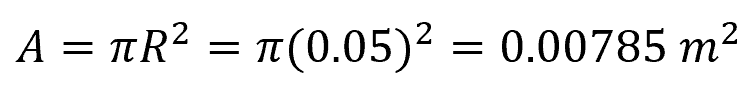
Calculating for the average shear stress:
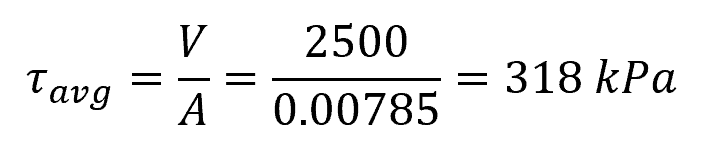
Therefore, the average shear stress in SI units is 318 kPa.
