The Tresca Yield Criterion is a theory of failure that can be used to predict the failure of ductile materials subjected to any type of loading.

It states that yielding or failure of a material subjected to multiaxial loading occurs when the maximum shear stress in the material reaches the shear stress that causes the same material to yield when loaded uniaxially.
Understanding the Tresca Yield Criterion
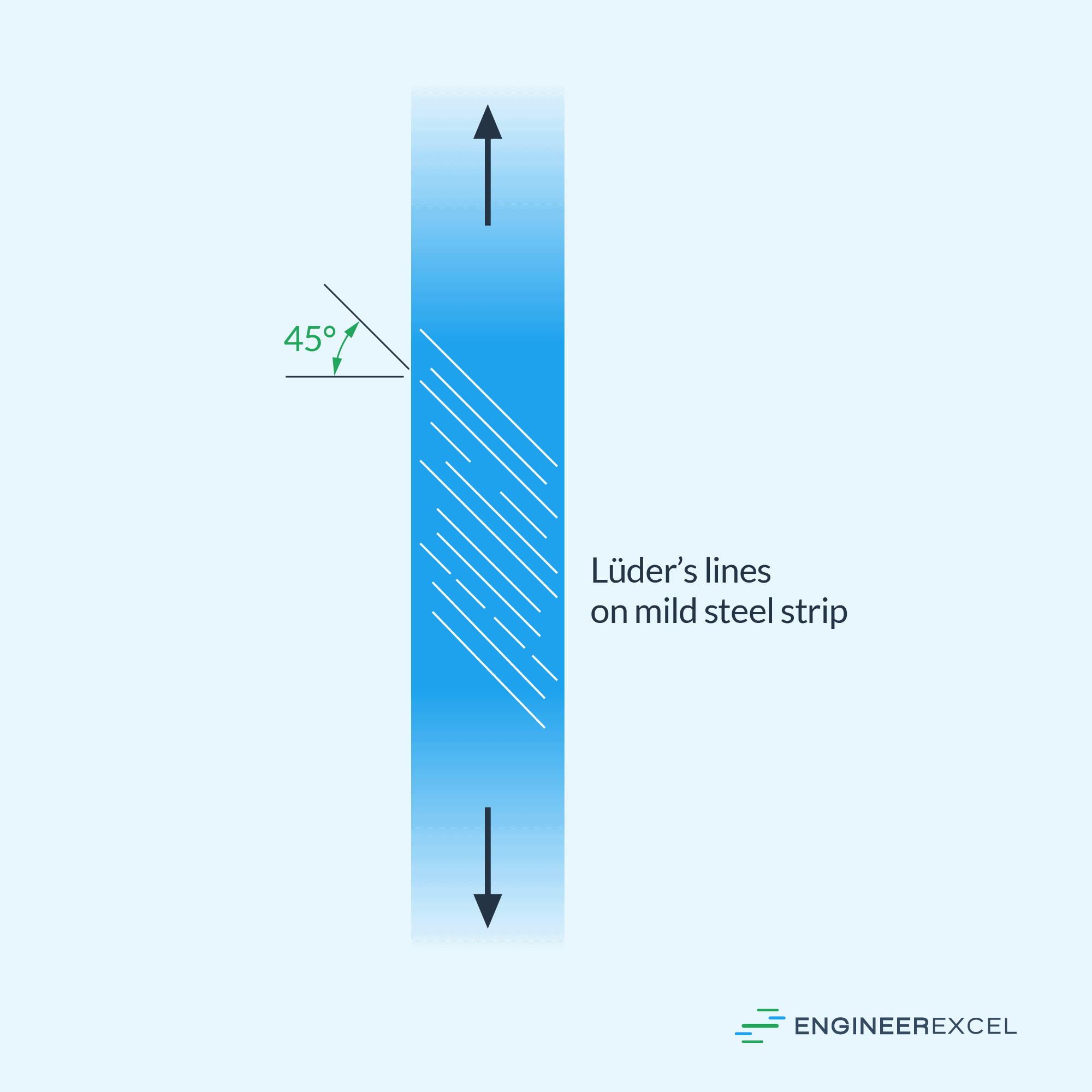
Ductile materials like steel typically experience yielding through slipping, which occurs due to shear stress along the contact planes of randomly ordered crystals that make up the material. The slip planes on the surface of the material, known as Lüder’s lines, are oriented at a 45-degree angle with respect to the strip’s axis, as shown in the diagram below.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
This concept forms the basis of the Tresca Yield Criterion, which is also known as the Maximum Shear Stress Theory.
The Tresca Yield Criterion is a theory of failure that specifically deals with the failure of ductile materials subjected to any type of loading. This criterion, developed by French engineer Henri Tresca in 1868, states that yielding occurs when the maximum shear stress in a material exceeds the shear stress that causes the same material to yield when it is subjected to uniaxial tension.
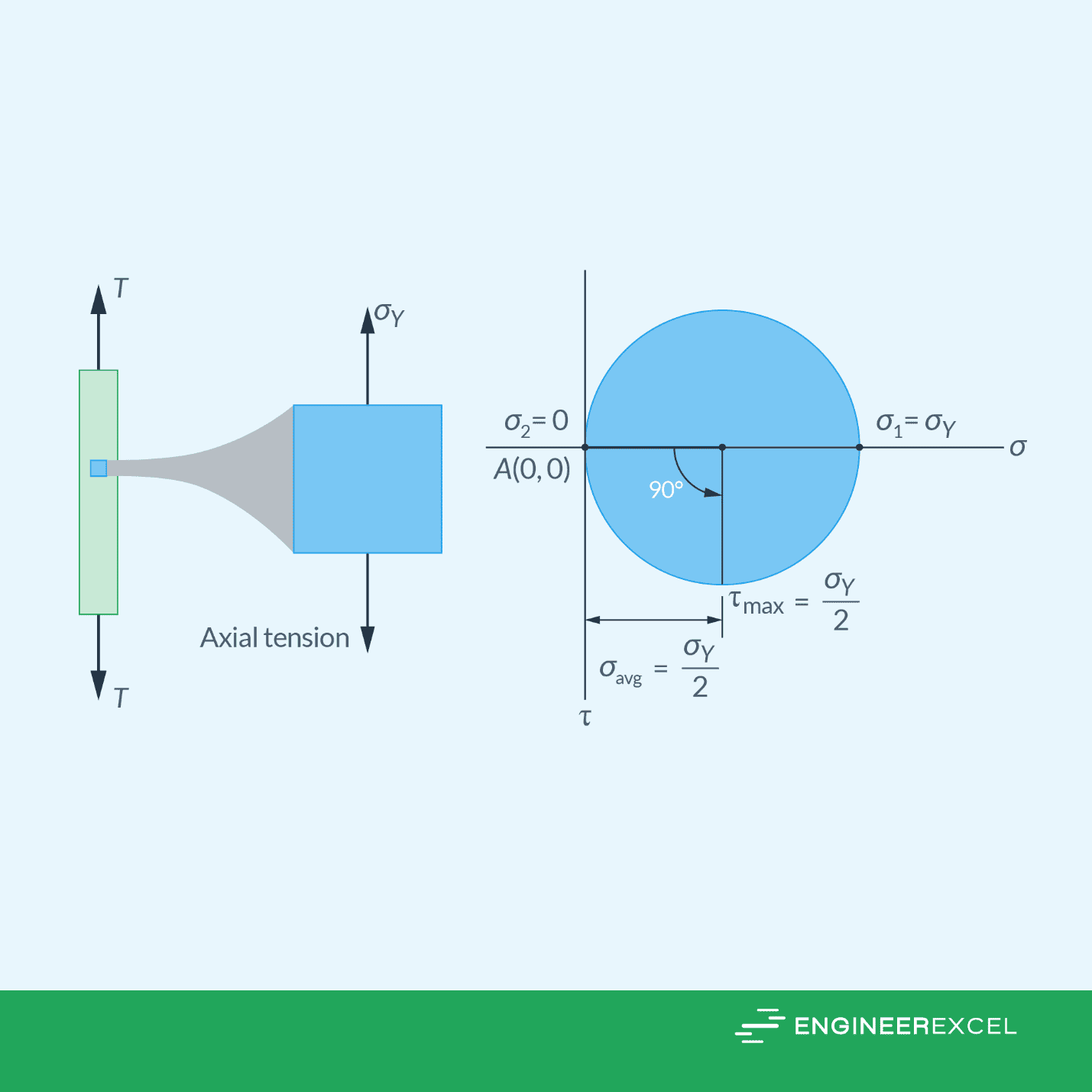
The shear stress that causes yielding in uniaxial tension is equal to half of the yield strength of the material, as shown in the Mohr’s circle above. Therefore, to avoid failure, it is required that the absolute maximum shear stress in the material must be less than or equal to half of the yield strength, where the yield strength is determined from a simple tension test.
It is important to note that the Tresca Yield Criterion does not consider hydrostatic stress or pressure. Therefore, it is most applicable in scenarios involving ductile materials such as metals, which typically fail under shear stresses caused by dislocation motion.
Equation for the Tresca Yield Criterion
In general, the Tresca yield criterion can be mathematically expressed as follows:
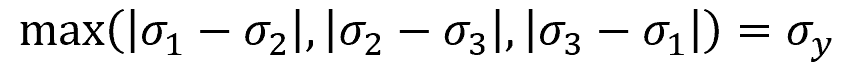
Where:
- σ1, σ2, σ3 = principal stresses [Pa]
- σy = yield strength of the material [Pa]
This can be visualized on a three-dimensional plane known as the Tresca Yield Envelope, shown below. This envelope represents the boundary that separates the elastic and plastic deformation regions of a material. For isotropic materials, meaning those with the same properties in every direction, the Tresca Yield Envelope has a distinctive hexagonal prismatic shape.

When the principal stresses (σ1, σ2, σ3) at a point in the material fall on the boundary or outside the envelope, the material is considered to have failed.
Tresca Yield Criterion in Plane Stress
For plane stress, the equation for the Tresca yield criterion can be simplified as follows:
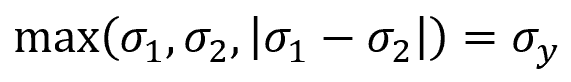
Graphically, this can be visualized using a two-dimensional hexagon, as shown below.
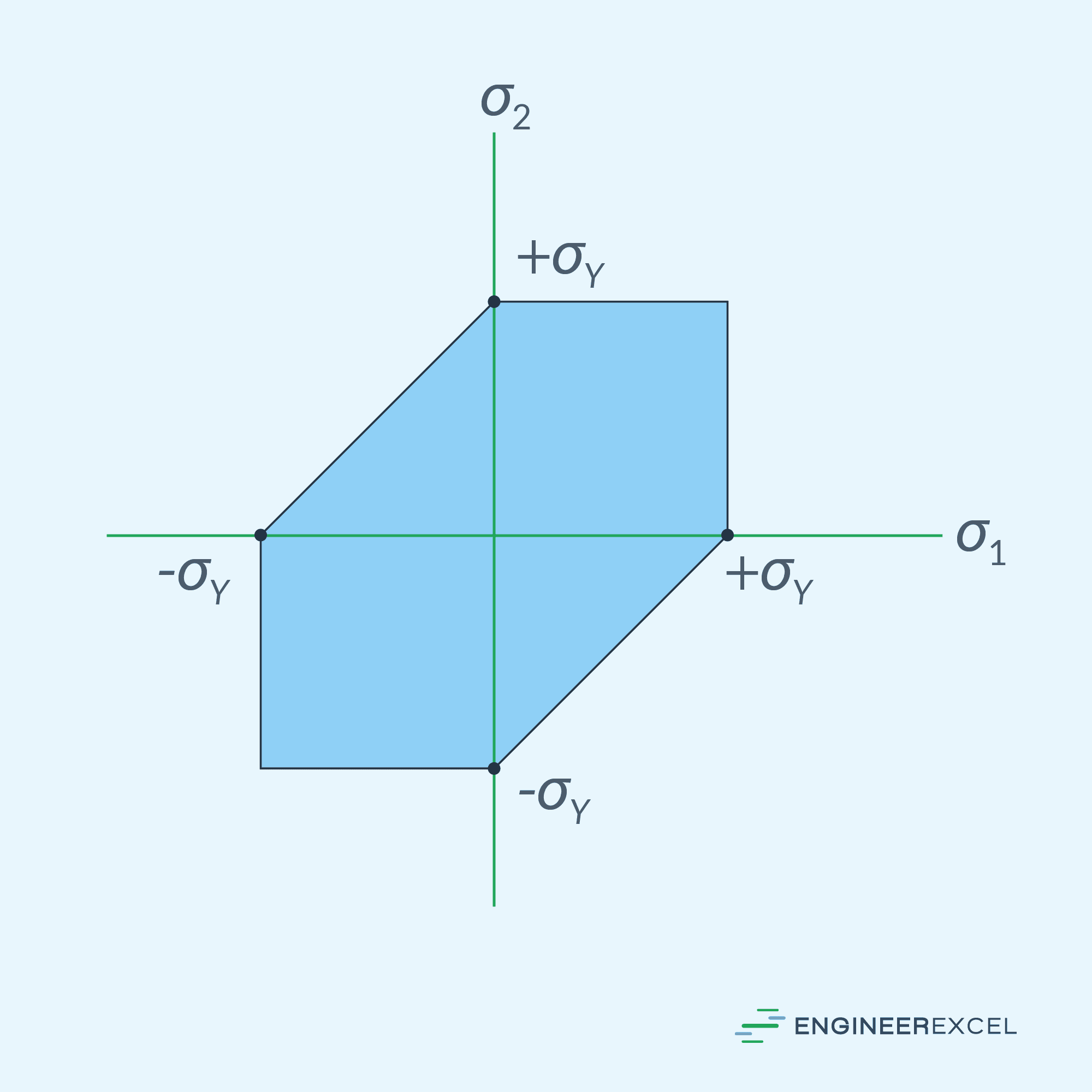
Tresca Criterion vs Von Mises Criterion
The Tresca Criterion and von Mises Criterion are both theories of failure that can be used for ductile materials. The von Mises theory is based on distortion energy, while the Tresca criterion is based on the concept that shear stress controls yielding.

The Tresca criterion was developed before the von Mises criterion. As shown in the diagram above, showing the von Mises and Tresca yield envelopes, the Tresca criterion is slightly more conservative in practice.
However, the von Mises criterion is the preferred theory, especially in pure shear. This is because actual torsion tests in a ductile specimen have shown that the von Mises criterion gives more accurate results for pure-shear failure than the Tresca criterion. In fact, the shear stress for yielding of the material as given by the von Mises criterion is about 15% more accurate than that given by the Tresca criterion.
Furthermore, although the Tresca criterion is easy to use in an analytical setting, it is not well suited for use in finite element codes due to the corners in the yield envelope.
