Supercritical flow in open channels occurs when the flow velocity exceeds the critical velocity, leading to water moving faster than waves can propagate. In this state, the flow is characterized by rapid fluid movement, and changes in channel geometry can result in hydraulic jumps.

In this article, we will discuss the characteristics, analysis, and applications of supercritical flow, including the Froude number for supercritical flow, wave propagation, specific energy, and examples of supercritical flow in various natural and engineered environments.
What is Supercritical Flow
In open channels, supercritical flow refers to the condition characterized by a rapid flow where fluid inertia dominates gravitational forces. This condition manifests when the flow’s speed is greater than the critical velocity, and the depth is shallower than the critical depth. This critical flow condition, which marks the transition between subcritical and supercritical flows, is generally described using the following equation:
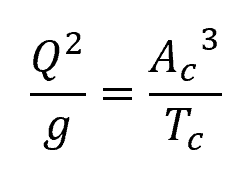

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Where:
- Q = flow rate [m3]
- g = gravitational acceleration [9.81 m/s2]
- Ac = cross-sectional flow area [m2]
- Tc = width of the channel section at the free surface [m]
Trial and error can be used to solve for the critical depth (yc) using the above equation. However, for common shapes, the critical depth can be determined from Ac and Tc using geometric relations.
From the critical depth, the critical velocity can be found using the following formula:
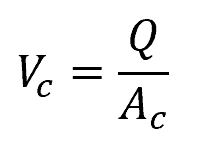
Where:
- Vc = critical flow velocity [m/s]
In supercritical flow, the water surface profiles are typically steep, and the flow is characterized by its fast-moving nature. This can result in uneven wave surface and can lead to increased erosion potential and hydraulic jumps, as shown in the diagram below.

Froude Number for Supercritical Flow
The Froude number is a dimensionless parameter used to characterize the flow regime in open channels. It is defined as the ratio of the flow velocity (V) to the wave celerity (c), with the wave celerity being the speed at which disturbances propagate in the flow.

Where:
- V = flow velocity [m/s]
- c = wave celerity [m/s]
- y = flow depth [m]
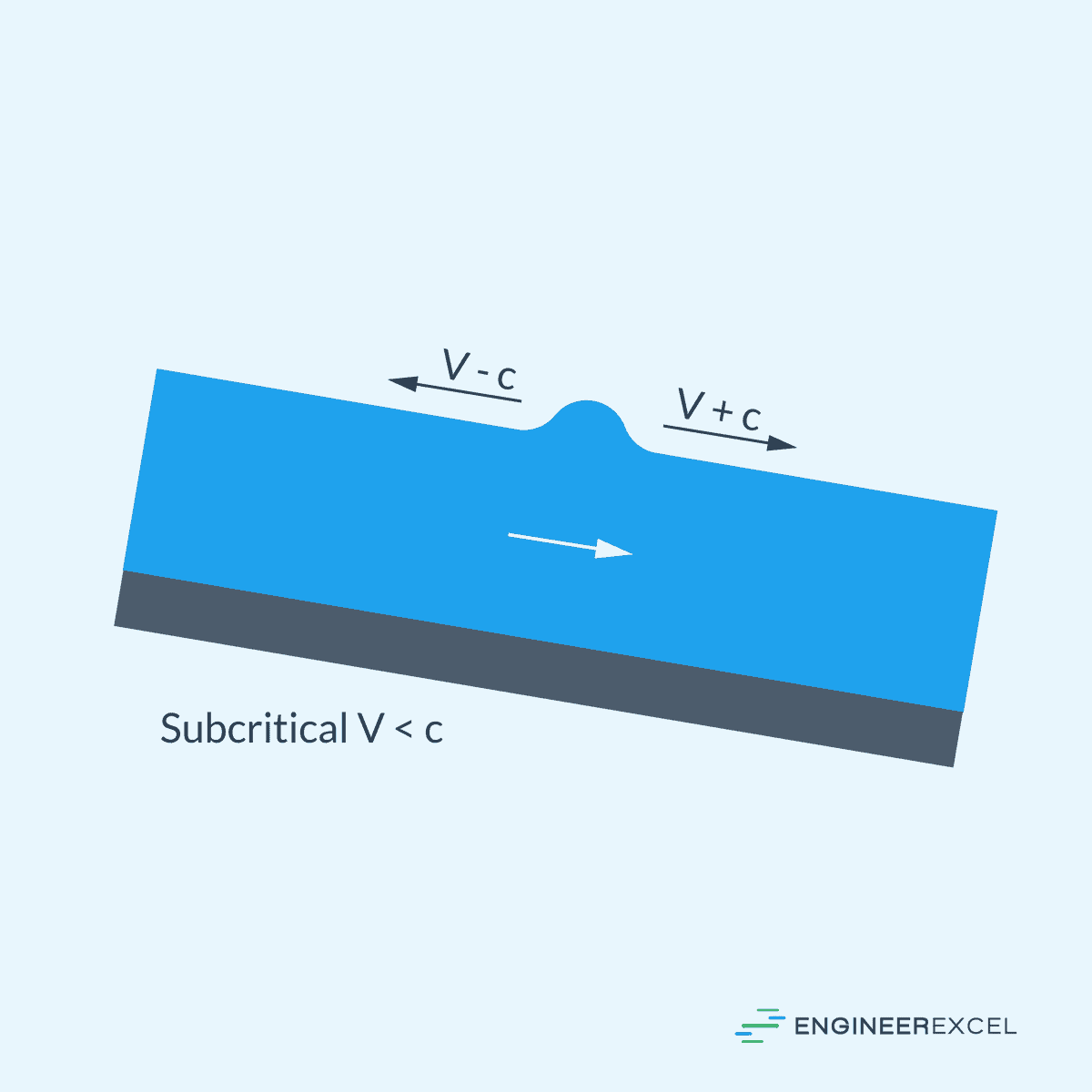
Supercritical flow in open channels occurs when the Froude number (Fr) is greater than 1. This means that the flow velocity is higher than the speed at which surface waves can move upstream.
As a result, the upstream and downstream ends travel at velocities (V − c) and (V + c) respectively in the downstream direction. In simple terms, supercritical flow carries the wave downstream and prevents it from traveling upstream, as illustrated in the diagram below.
Specific Energy of Supercritical Flow
Specific energy is the total energy relative to the channel bottom per unit weight of fluid. It is given by the equation:
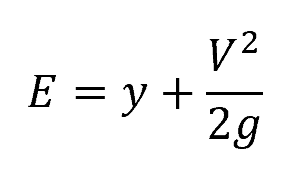
Where:
- E = specific energy [m]
For a given discharge, the specific energy can be plotted against flow depth, as shown in the diagram below.

In this diagram, the supercritical region is the region below the critical point, indicated by point (Emin, yc), where the specific energy reaches a minimum value.
Examples of Supercritical Flow
Mountain Streams
Steep mountain streams or rivers with a significant gradient can exhibit supercritical flow. Especially during flood events, rivers may experience supercritical flow due to the increased discharge and velocity. Floodwaters can accelerate and result in supercritical conditions, especially in narrow and steep sections of rivers.
Waterfalls and Cascades
When water descends over waterfalls or cascades, the flow often becomes supercritical due to the steep slope and sudden changes in elevation.
River Confluences
When two rivers with different flow velocities or discharges converge, the interaction of the flows can result in supercritical conditions, particularly in the downstream reach of the confluence.
Dam Outflows
The discharge from a dam can result in supercritical flow conditions downstream. The rapid release of water can generate high velocities, especially in steep channels, and cause supercritical flow until the conditions gradually stabilize.
Tidal Bores
In estuaries or rivers experiencing tidal influences, tidal bores can create supercritical flow conditions. Tidal bores are surges of water that propagate upstream against the river current during high tide.
Example Problem
Problem: A rectangular channel has a width (b) of 2 meters and a depth (y) of 3 meters. The flow rate through the channel is 40 cubic meters per second. Is the flow supercritical?
Solution:
The Froude number (Fr) in an open channel is given by the formula:
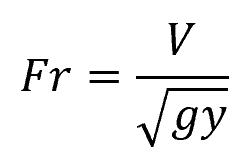
First, we need to calculate the flow velocity (V) using the flow rate and channel dimensions:
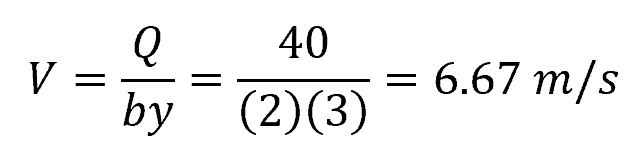
Now, we can calculate the Froude number using the flow velocity and flow depth:
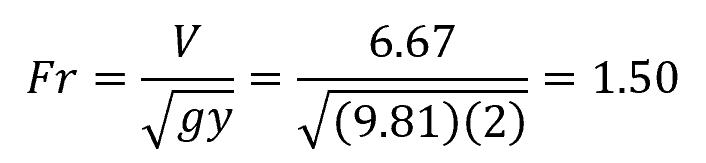
Since the Froude number is greater than 1, therefore, the flow is supercritical.
