Poiseuille flow describes the steady, laminar flow of an incompressible, viscous fluid through a cylindrical pipe or tube. It is a valuable concept in fluid mechanics used in various engineering and scientific applications, such as the design of pipelines, blood flow in arteries, and the flow of gases in microchannels.

In this article, we discuss the key principles and applications of Poiseuille flow in fluid dynamics, including the Hagen-Poiseuille law and Poiseuille flow calculations.
Poiseuille Flow Explained
Poiseuille flow, also known as Hagen-Poiseuille flow, refers to the steady, axisymmetric flow of a fluid inside a long, circular pipe with a constant radius. This flow is generated by a pressure gradient in the axial direction and is constrained by the pipe’s walls, leading to a parabolic velocity profile. This flow is named after two scientists, Jean Leonard Marie Poiseuille and Gotthilf Hagen, who independently conducted experiments and derived equations related to fluid dynamics in the 19th century.
The assumptions used in deriving Poiseuille flow include incompressible fluid, steady-state flow, and negligible gravitational effects. Based on these assumptions, the Navier-Stokes equation, which governs the momentum balance in fluids, reduces to a simplified form suitable for analyzing the flow inside the pipe.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
The pressure-driven nature of Poiseuille flow results in the fluid being subjected to friction between the fluid layers and the pipe wall. Due to these interactions, the fluid’s velocity ranges from zero at the pipe wall to the maximum at the pipe’s center, resulting in a parabolic velocity profile. This is illustrated in the diagram below.
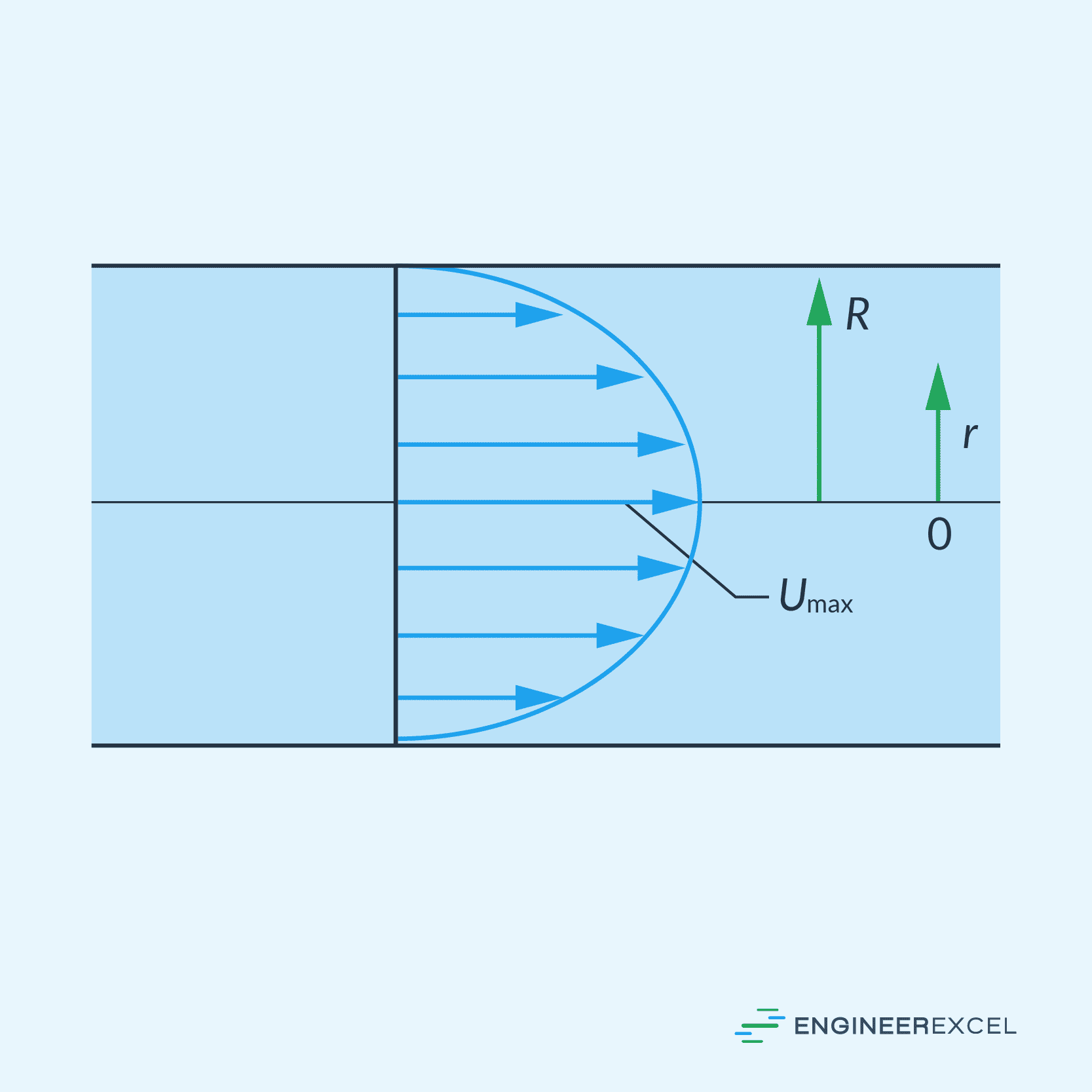
The behavior of the flow follows the Hagen-Poiseuille law, which quantifies the relationship between pressure gradient, pipe dimensions, fluid velocity, and viscosity, as shown in the following equation:
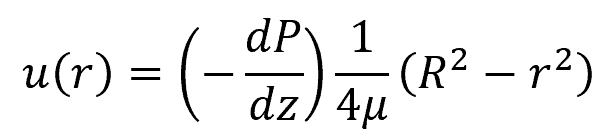
Where:
- u(r) = fluid’s axial velocity as a function of radial distance from pipe center [m/s]
- r = radial distance from pipe center [m]
- dP/dz = pressure gradient along the axial direction [Pa/m]
- µ = fluid’s dynamic viscosity [Pa-s]
- R = pipe radius [m]
Poiseuille Flow Calculations
Maximum Flow Velocity
Given the velocity distribution, the maximum velocity at the center of the pipe can be found by calculating for the velocity at r=0:
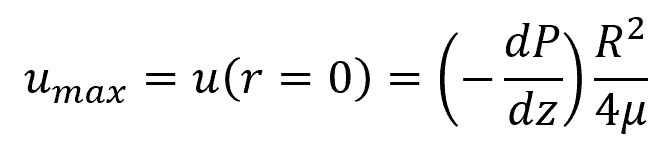
Where:
- umax = maximum flow velocity [m/s]
Flow Rate
The flow rate describes the volume of fluid passing through the pipe per unit of time. It can be found by integrating the velocity equation across the whole cross-sectional area of the flow:
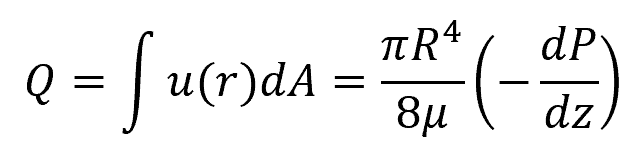
For a pipe with a finite length and known pressure drop, the above equation can be expressed as:
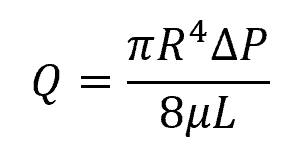
Where:
- Q = flow rate [m3/s]
- ΔP = pressure drop across the pipe length [Pa]
- L = length of pipe [m]
Average Flow Velocity
The average velocity can be found by dividing the flow rate by the flow area:
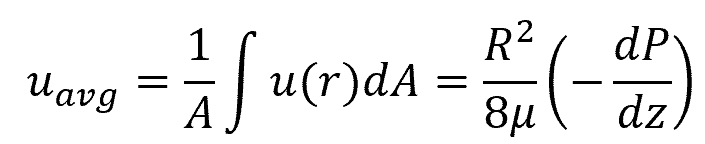
Note that this is also equal to one-half of the maximum velocity. For a finite pipe length, the average velocity can be calculated using the following formula:
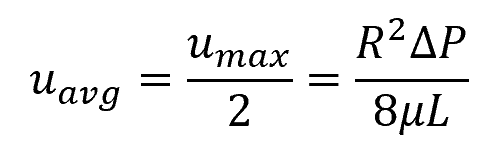
Where:
- uavg = average flow velocity [m/s]
Wall Shear Stress
The wall shear stress represents the force exerted by the fluid on the inner walls of the pipe. It can be calculated by multiplying the fluid viscosity with the radial velocity gradient at the pipe wall:
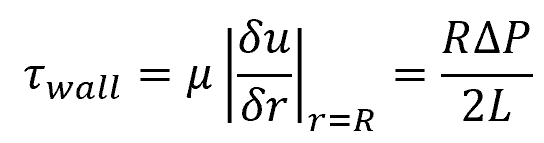
Where:
- τwall = wall shear stress [Pa]
Applications of Poiseuille Flow
Poiseuille flow has numerous applications in various fields such as engineering, medicine, and environmental science.
In engineering, Poiseuille flow is fundamental for the design and optimization of fluid transport systems, such as pipelines, lubrication systems, and microfluidic devices. Transporting fluids like oil, water, and chemicals through pipelines uses the principles of Poiseuille flow to predict the fluid’s laminar velocity profile, pressure drop, and pumping requirements.

In medicine, Poiseuille flow is relevant to blood flow in small vessels and capillaries. The blood vessels in our body are essentially biological tubes where blood flows due to the pressure difference created by the heart’s pumping action. The knowledge of Poiseuille flow is critical for designing medical devices like catheters and stents, which are used to facilitate and regulate blood flow in patients with vascular diseases.
Environmental applications of Poiseuille flow include monitoring and controlling groundwater flow. In aquifers, water moves through porous media due to a pressure gradient, and understanding Poiseuille flow can help predict the transport of contaminants and develop remediation strategies. Furthermore, it is essential in studying the movement of fluids through soil and sediment layers, impacting natural processes like nutrient cycling and pollutant transport.
