When studying fluid dynamics, you might come across two seemingly similar terms: streamline flow and laminar flow. Both of these concepts describe the motion of fluid particles within their respective systems. However, the question arises: are these two terms actually the same?
Are Streamline Flow and Laminar Flow the Same?
Both streamline flow and laminar flow describe fluid movement. In streamlined flow, the fluid particles flow parallel to each other, and the path taken by a particle at a specific point is identical to the path taken by the preceding particle at that point.

This results in a smooth, streamlined flow that is often visualized as a bundle of streams called a stream tube, where fluid particles do not cross the surface of the tube.


Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Laminar flow is also closely related to and sometimes used interchangeably with streamline flow. It too refers to the smooth, parallel flow of fluid particles, which move in a consistent, coordinated manner—instead of exhibiting chaotic or random behavior. Laminar flow often occurs at low fluid velocities, and its primary characteristic is the absence of turbulence that accompanies fast-moving fluid.
Although at first glance, laminar flow and streamline flow may appear to be the same, there is a subtle distinction between the two. Streamline flow specifically describes the movement of particles within individual paths, called streamlines, while laminar flow emphasizes the overall smooth and orderly nature of the fluid flow. In practice, however, streamline flow and laminar flow are often used to describe the same phenomenon due to their shared characteristics and behavior in certain fluid motion scenarios.
Characterizing Streamline or Laminar Flow
Laminar flow or streamlined flow is characterized by a smooth, orderly, and well-organized flow pattern in which fluid particles move in parallel layers or streamlines, with minimal mixing between adjacent layers. In this type of flow, the fluid’s velocity varies from zero at the walls to a maximum value along the centerline of the pipe or tube it is flowing through. This creates a parabolic velocity profile, as illustrated in the diagram below.
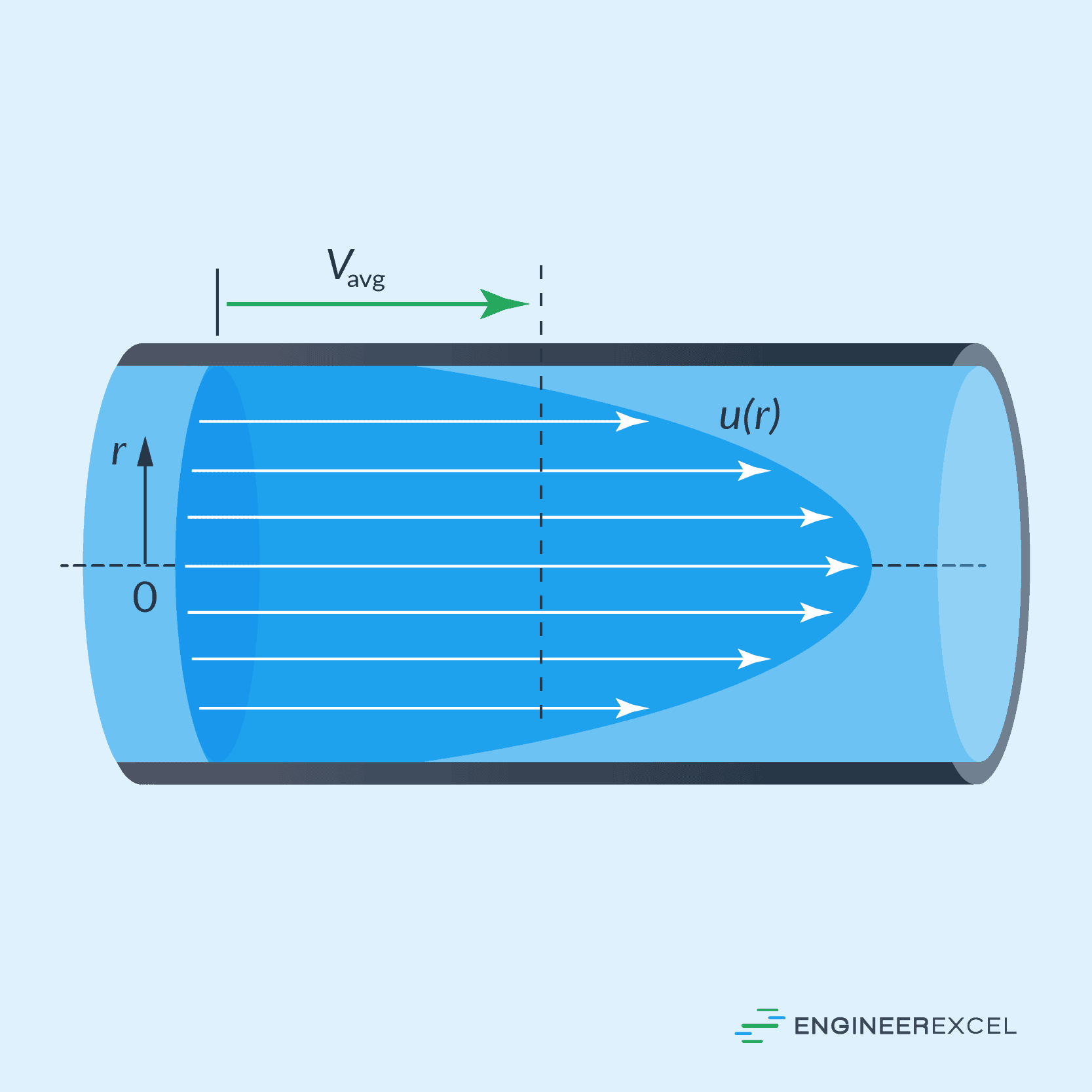
The flow profile in a pipe can be calculated by dividing it into thin, cylindrical elements and then applying the viscous force to them. This method allows for the prediction of the fluid’s behavior under laminar flow conditions. In contrast, when the fluid layers break up into turbulence, modeling becomes significantly more difficult.
Laminar flow generally has lower flow resistance or frictional losses compared to turbulent flow. This makes it more energy-efficient for some applications. It also provides a more predictable and controlled heat transfer rate, which is advantageous in applications such as heat exchangers.
In addition, laminar flow is quieter and generates fewer vibrations compared to turbulent flow. However, it is less effective at mixing substances within the fluid, which may be a disadvantage in certain chemical processes.

An important factor for determining whether a flow would be laminar is the Reynolds number. This dimensionless number compares the inertial forces to viscous forces within the fluid and acts as a criterion for characterizing flow patterns.
The Reynolds number can be calculated using the following formula:
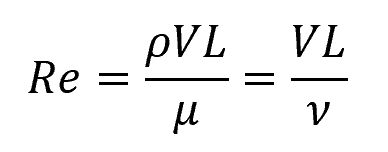
Where:
- Re = Reynolds number [unitless]
- ρ = density of the fluid [kg/m3]
- V = velocity of the fluid [m/s]
- L = characteristic length of the flow [m]
- μ = dynamic viscosity of the fluid [Pa-s]
- ν = kinematic viscosity of the fluid [m2/s]
To achieve laminar flow, you need to maintain a small Reynolds number value. This can be done by keeping the fluid velocity and characteristic length low, or by increasing the fluid’s viscosity.
In general, laminar flow occurs at Reynolds numbers ranging from 0 to 103. For pipe flows, specifically, laminar flow happens at Reynolds numbers below 2300. Beyond this value, the flow starts to transition to turbulent flow and is fully turbulent when Re > 4000.
It is important to note that this critical value is only applicable to circular pipe flows. Other geometries, like plates and airfoils, have entirely different transition Reynolds numbers.
In practice, fluid systems exhibit a transitional regime between laminar and turbulent flow, where both laminar and turbulent characteristics may coexist. Understanding the flow regime and its implications is essential for designing and optimizing various engineering and scientific applications, such as pipelines, chemical reactors, and aerodynamics.
