Fluid dynamics presents two primary types of flow: laminar and turbulent. Understanding the characteristics and implications of these flow patterns is essential for predicting and controlling fluid behavior in engineering applications.

Laminar flow is smooth and predictable, creating minimal frictional forces, while turbulent flow is chaotic and irregular, causing increased energy dissipation and drag. Discover the characteristics and implications of these flow patterns below.
Definition Of Flows
Laminar flow occurs when a fluid flows smoothly in parallel layers without any significant mixing. In this type of flow, you can observe the fluid moving in straight lines, with the velocity increasing towards the center of the flow. This creates a predictable, steady environment where fluid resistance is relatively low.
On the other hand, turbulent flow is characterized by chaotic and irregular movement of fluid particles. You can observe fluid mixing, swirling, and forming eddies or vortices in a turbulent flow. The flow can be highly unpredictable, and fluid resistance is typically higher than in laminar flow.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
The transition between laminar and turbulent flow is primarily governed by a dimensionless parameter called the Reynolds number (Re). A low Reynolds number (Re < 2000) indicates laminar flow, whereas a high Reynolds number (Re > 4000) signifies turbulent flow. For 2000 < Re < 4000, the flow is in a transitional state.
In practical applications, you might encounter the following key features:
- In laminar flow:
- Fluid flow is smooth and ordered.
- Frictional losses are minimized.
- Noise and vibrations are reduced.
- In turbulent flow:
- Fluid flow is chaotic and disordered.
- Friction losses are increased.
- Noise and vibrations may be significant.

Characteristics of Laminar and Turbulent Flow
Laminar Flow Characteristics
Laminar flow occurs when a fluid flows smoothly in parallel layers with minimal mixing or disturbances between them. In this flow regime, you can observe the following characteristics:
- Low velocity: Laminar flow typically manifests at low velocities or in situations with low Reynolds numbers (Re < 2000).
- Low pressure drop: Due to its smooth, orderly nature, laminar flow results in minimal frictional losses and a lower pressure drop across the flow path.
- Predictable motion: You can easily predict and analyze the flow pattern using mathematical models. This is because each fluid particle moves along a streamline in a gradual, organized manner.
Turbulent Flow Characteristics
Turbulent flow, on the other hand, is characterized by chaotic, irregular fluid motion with rapid fluctuations in speed and direction. Key traits of turbulent flow include:
- High velocity: Turbulent flow often arises at high fluid velocities or in scenarios with high Reynolds numbers (Re > 4000).
- Increased pressure drop: Turbulent flow creates significant viscous and pressure drag, causing a higher pressure drop across the flow path.
- Enhanced mixing: The chaotic fluctuations in velocity and direction facilitate a rapid mixing of fluid particles, promoting efficient heat and mass transfer in engineering applications.
Mathematical Modeling of Flows
Laminar Flow Equations
Laminar flow, characterized by smooth and orderly motion, can be described mathematically using the Navier-Stokes equations. These equations govern fluid dynamics and allow you to calculate velocity, pressure, and other important variables.
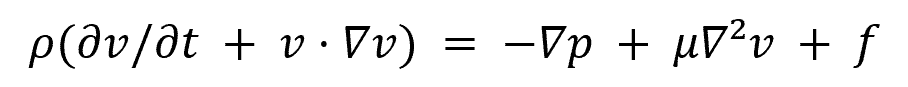
where ρ is the fluid density, v is the velocity vector, t is time, p is the pressure, μ is the dynamic viscosity, ∇ is the gradient operator, and f is any external force acting on the fluid.
Certain assumptions can be made for simplification, such as incompressible fluids, steady-state conditions, and negligible body forces.
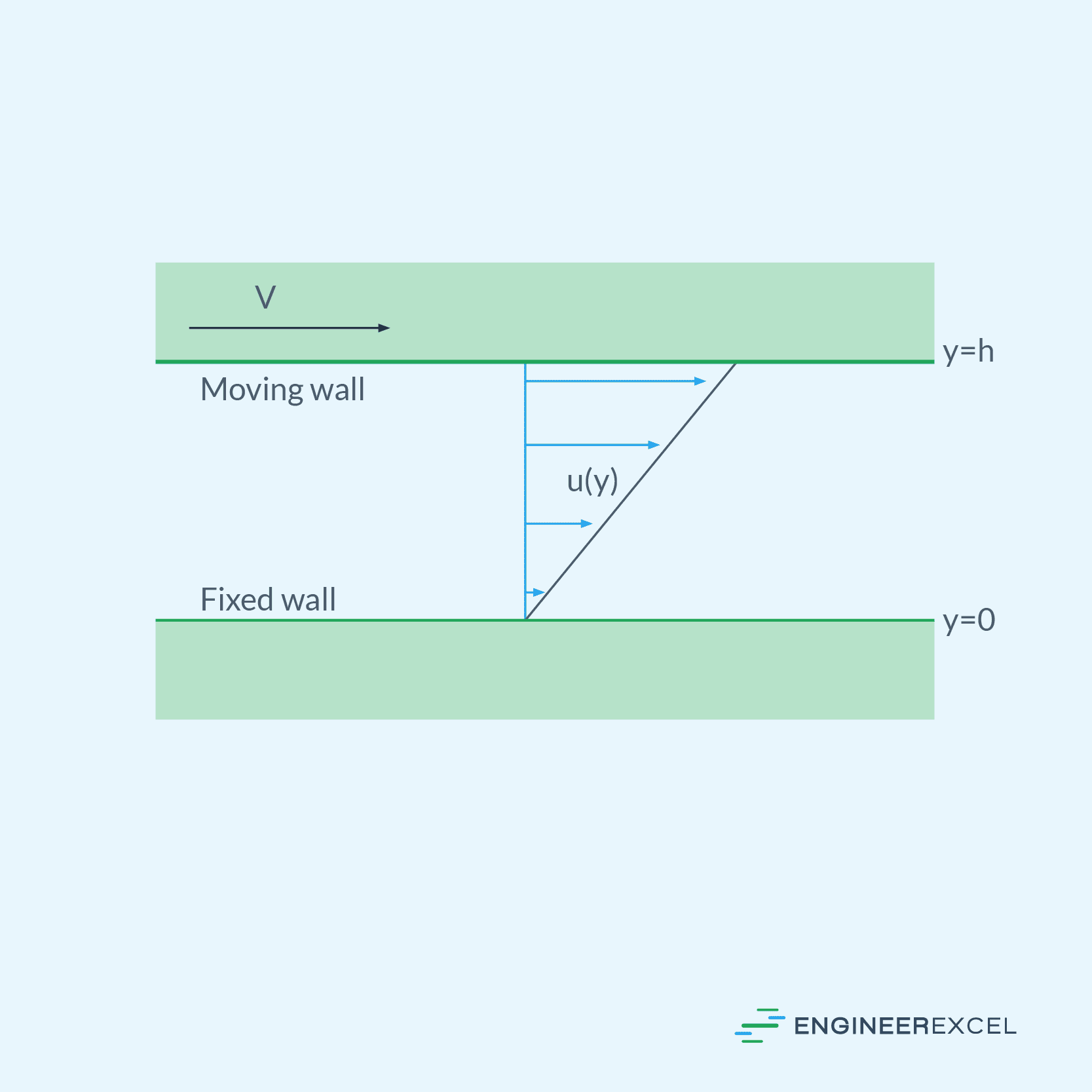
One common laminar flow type is Couette flow, which is observed between two parallel plates. In this scenario, you can apply the no-slip boundary condition and take advantage of the linearity of the Navier-Stokes equations to solve for fluid characteristics:
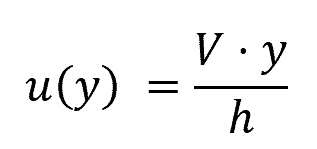
where u(y) is the velocity of the fluid at height y, V is the velocity of the top plate, and h is the distance between the plates.
Turbulent Flow Equations
Turbulent flow, characterized by chaotic and random motion, presents a greater challenge to model mathematically. The Reynolds-averaged Navier-Stokes (RANS) equations predict turbulent flow behavior. These equations introduce additional transport variables, accounting for the fluctuations in fluid properties.
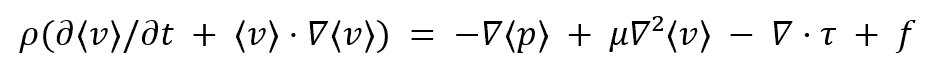
where ρ is the fluid density, ⟨v⟩ is the time-averaged velocity vector, t is time, ⟨p⟩ is the time-averaged pressure, μ is the dynamic viscosity, ∇ is the gradient operator, τ is the Reynolds stress tensor, and f is any external force acting on the fluid.
The Reynolds stress tensor must be modeled separately using turbulence models, such as the k-ε or k-ω models. However, the appropriate turbulence model is situationally dependent, as each has assumptions and limitations. In general, computational fluid dynamics (CFD) software can be a valuable tool for investigating both laminar and turbulent flows.
Applications and Examples
Laminar Flow Applications
In aerospace engineering, laminar flow reduces drag on aircraft wings and fuselages. Designs like the NACA airfoils help maintain this smooth flow, improving fuel efficiency and overall performance.

In microfluidics, laminar flow is beneficial, as it allows precise control over the movement of fluids through microchannels. This is especially useful in lab-on-a-chip devices and chemical reactors.
Moreover, the biomedical industry uses laminar flow in operating rooms and clean rooms, where air filtration systems minimize airborne contaminants to create a sterile environment.
Turbulent Flow Applications
In heat exchangers, turbulent flow promotes faster energy transfer between fluid mediums, leading to improved efficiency. You can observe this in shell-and-tube heat exchangers and the cooling systems of internal combustion engines.
Water treatment facilities employ turbulent flow to enhance mixing in flocculation and coagulation phases. Turbulence ensures uniform distribution of chemicals, making the process more effective.
The turbomachinery industry uses turbulent flow in pumps, turbines, and compressors. The improved mixing properties and energy transfer capabilities enable higher efficiency in these devices.
Factors Influencing Laminar and Turbulent Flow
When analyzing fluid flow, two key factors typically affect whether it becomes laminar or turbulent: Reynolds number and flow geometry.
Reynolds number is a dimensionless quantity given by the formula
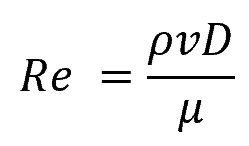
where ρ is fluid density, v is flow velocity, D is the characteristic length (such as pipe diameter), and μ is fluid viscosity. Laminar flow generally occurs at a Reynolds number below 2,000, while turbulent flow tends to occur above 4,000. The regime between 2,000 and 4,000 is sometimes called the transition zone.
- Increasing fluid velocity or decreasing fluid viscosity will result in higher Reynolds numbers, leading to a greater likelihood of turbulent flow.
- Similarly, larger characteristic lengths (e.g., pipe diameter) will increase the Reynolds number and promote turbulence.
Flow geometry deals with the physical layout of the system through which the fluid flows. Disruptions in flow geometry can trigger turbulence, even at low Reynolds numbers. Examples of disruptions include:
- Abrupt changes in pipe diameter or direction
- The presence of obstacles such as bends, valves, or in-pipe equipment
- Surface roughness of the walls through which fluid flows
Optimize your system design and use smoother, streamlined surfaces to minimize flow disruptions and maintain laminar flow.
Transition and Prediction of Flow Regimes
When studying fluid dynamics, you’ll encounter two main flow regimes: laminar and turbulent. Laminar flow is characterized by smooth, orderly motion, while turbulent flow consists of random fluctuations and is more chaotic. You may observe laminar flow when water flows slowly out of a faucet, and turbulent flow near fire hydrants or smokestacks, as described in this explanation of Transition and Turbulence.
As an engineer, you might be interested in controlling or predicting these flow regimes to optimize a design or prevent issues. For instance, in a pipe system, a laminar flow could result in less friction loss, while a turbulent flow could be beneficial for mixing purposes.
Additionally, shear stress and pressure drop are essential factors that you must consider when working with fluid dynamics, as they also impact flow regimes. Close attention to these factors will help you design more efficient systems, minimizing energy losses and ensuring optimal operation.
Understanding the transition points between laminar and turbulent flow is crucial for engineers and engineering students. By utilizing the Reynolds number and considering shear stress and pressure drop, you can accurately predict and optimize various flow regimes in your work.
