It is important to understand the connection between fluid flow rate and pressure difference across a pipe in various fluid mechanics applications. The Hagen-Poiseuille equation is frequently utilized to describe this relationship, especially for laminar flows.

However, in this article, we will delve into how this equation can be applied for turbulent flows.
Understanding The Hagen Poiseuille Equation
In fluid dynamics, the Hagen-Poiseuille equation describes the relationship between the flow rate, pressure drop, length and size of pipe, and fluid viscosity in laminar flow of Newtonian fluids. It is named after two physicists, Gotthilf Hagen and Jean Leonard Marie Poiseuille, who independently derived the equation in the mid-19th century.
In 1839, Hagen conducted experiments on the flow of water through pipes of different diameters and lengths. He observed that the rate of flow was proportional to the fourth power of the pipe radius and inversely proportional to the length of the pipe. However, he did not take into account the effect of fluid viscosity on the flow rate.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
In 1840, Poiseuille conducted similar experiments on the flow of blood through capillaries and small tubes. He observed that the rate of flow was proportional to the pressure difference between the two ends of the tube, the fourth power of the tube radius, and inversely proportional to the viscosity of the fluid and the length of the tube. Poiseuille’s work was more comprehensive than Hagen’s and included the effect of viscosity on the flow rate.
In 1845, Poiseuille published his findings in a paper. However, it was not until later that the equation became known as the Hagen-Poiseuille equation, as Hagen’s work was rediscovered and incorporated into the equation.
To help understand this concept, consider the diagram below showing a viscous fluid moving through a horizontal pipe due to a pressure difference.
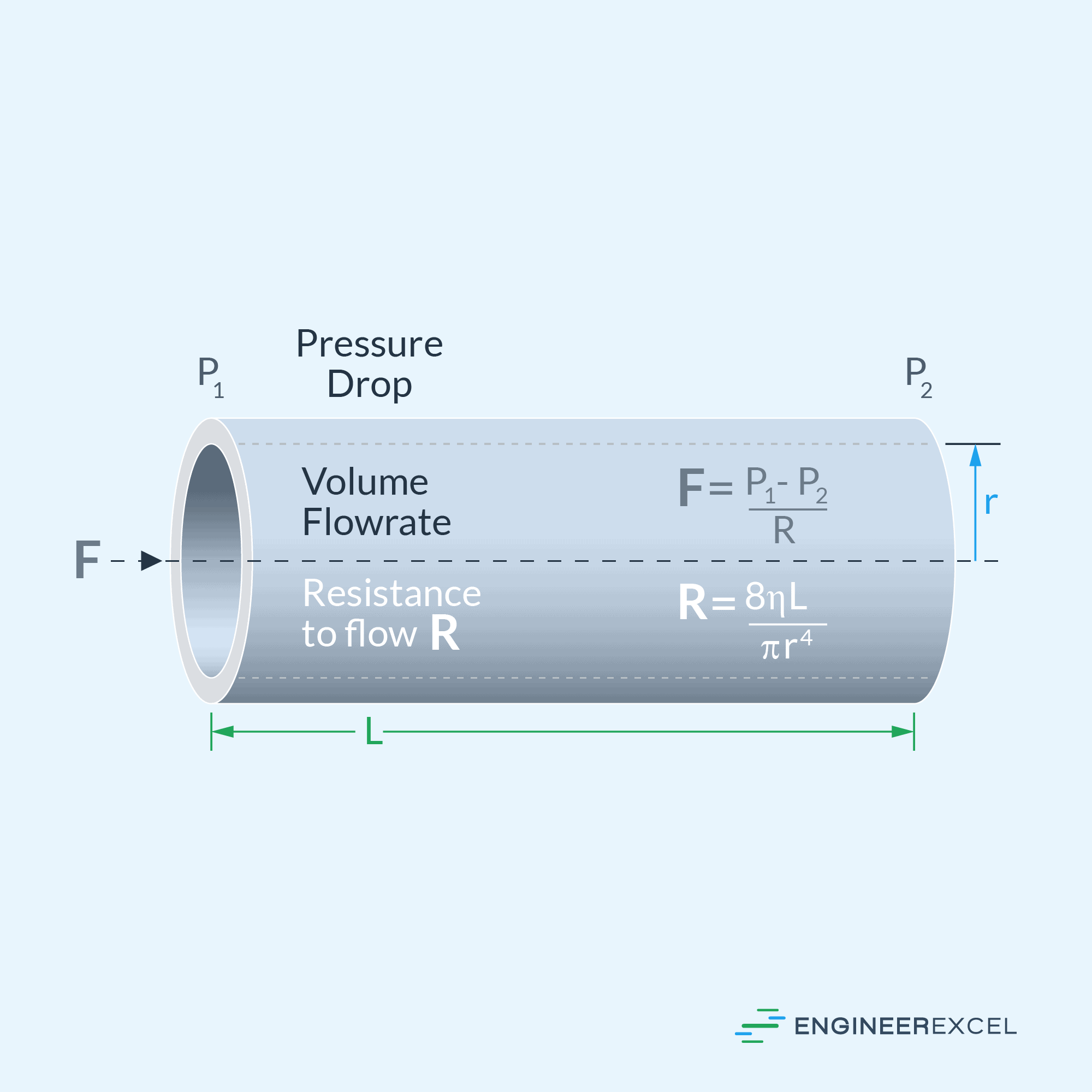
To derive the Hagen-Poiseuille equation, consider a steady state flow of an incompressible fluid through a straight pipe of constant radius. Apply the Navier-Stokes equation along the axial direction, assuming no changes in flow velocity and pressure due to gravity.
The fluid motion is driven by the pressure gradient. You can create a force balance between the viscous forces resulting from the pressure difference and the shear stress of the fluid. By integrating twice over the radial distance and applying the no-slip boundary condition on the pipe wall, the axial velocity profile is obtained.
The volumetric flow rate can be calculated by integrating the velocity profile over the whole pipe cross-section. This leads to the final Hagen-Poiseuille equation, which relates the volumetric flow rate, pressure drop, pipe length, and pipe size.
The Hagen-Poiseuille equation can be written as follows:
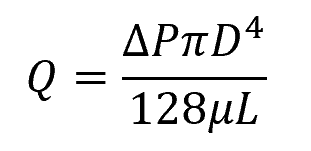
Where:
- Q = volumetric flow rate [m3/s]
- ΔP = pressure difference between the two ends of the pipe [Pa or N/m2]
- D = diameter of the pipe [m]
- μ = dynamic viscosity of the fluid [Pa-s]
- L = length of the pipe [m]
For laminar flows, the Hagen-Poiseuille equation states that as the pressure difference between the two ends of the pipe increases, the flow rate increases, and vice versa. Moreover, the flow rate is directly proportional to the fourth power of the diameter of the pipe, and inversely proportional to the length of the pipe and the viscosity of the fluid.
Applicability Of Hagen Poiseuille Equation To Turbulent Flow
The Hagen-Poiseuille equation is specifically applicable only when flow is laminar, and the pipe is relatively long and narrow. Under these conditions, turbulent effects are negligible and the assumption of steady, incompressible flow can be made.

When dealing with turbulent flow, the equation becomes less accurate. This is because it was initially derived for laminar flow, where fluid layers maintain a consistent velocity profile. In turbulent flow, fluid movements may become chaotic and unpredictable, which is inconsistent with the assumptions of the equation.
Nonetheless, the Hagen-Poiseuille equation can still be used to gain valuable insights into the relationship between the pressure drop and flow rate of a turbulent pipe flow. The equation can be extended to turbulent flow by inferring an effective turbulent viscosity, even though the flow profile in turbulent flow is not actually parabolic.
However, it is more common to utilize the Darcy-Weisbach equation along with the Moody chart for improved accuracy in the turbulent flow regime. These alternative models are based on the principle of frictional losses in a fluid flowing through a pipe or channel.
The Darcy-Weisbach equation relates the frictional head loss to the flow rate, pipe diameter, fluid density, and viscosity, as shown in the equation below. It is commonly used in engineering applications for calculating pressure drop in pipes and ducts.

Where:
- hL = head loss due to friction [m]
- fD = Darcy friction factor [unitless]
- v = mean fluid velocity [m/s]
- g = gravitational constant [9.81 m/s2]
