The Bernoulli Equation is one of fluid mechanic’s classic equations, used for hundreds of years to calculate idealized flows. The equation is essentially an application of the law of conservation of energy, used to track pressure and flow changes. However, because of the viscous, unsteady, and irreversible nature of turbulent flows, Bernoulli’s equation is largely unusable to study them.
What is the Bernoulli Equation?
The ideas behind the Bernoulli Equation were first postulated by Daniel Bernoulli in his book Hydrodynamica in 1738. His hypothesis and subsequent experiments to prove it showed that internal pressure of a fluid will decrease as the velocity increases. The specific and now famous Bernoulli equation, however, was later derived from this principle by Leonard Euler in 1752.
The equation is as follows:
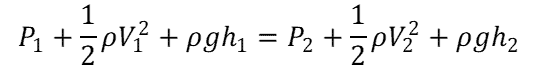
where:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
- P = pressure energy (Pa)
- ρ = fluid density (kg/m3)
- V = fluid velocity (m/s)
- g = gravitational acceleration (m/s2)
- h = height relative to a given reference plane (m)
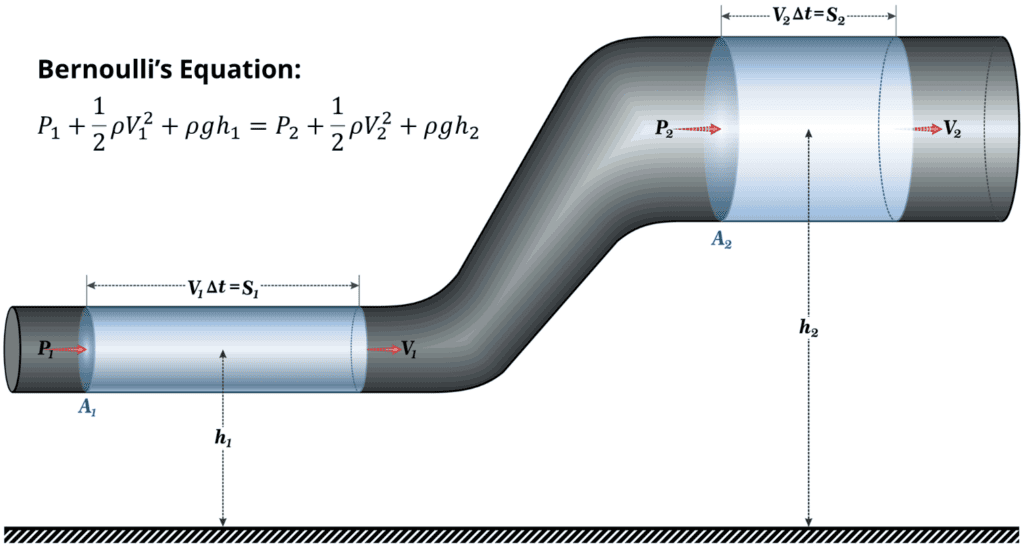
Here we the sides of the equation, denoted with subscripts (1) and (2), represent different portions of the pipe or fluid flow. Typical uses of the Bernoulli equation solving for a particular term such as velocity or pressure as the fluid moves through a pipe of differing area or height.
The righthand side of the equation is also said to constant, as energy is conserved throughout the length of the pipe, stream, or whatever type flow is being studied. The different terms on each side of the equation can be thought of as different kinds of energy that contribute to a fluid’s overall state. Since energy is conserved, as these terms change value, they will do so in a matter that will add up to the same total energy value.
- P can be thought of as the “pressure energy” of the system, a sort of vague term that includes the thermal, molecular kinetic energy of each unit of the fluid. It is also known as the mechanical energy, or “work”, of a fluid.
- ½ρv2 encompasses the kinetic energy of the fluid, i.e. the energy the fluid has because it is moving (note that this term includes the fluid’s velocity).
- ρgh is a fluid’s potential energy. The h term indicates how high above a reference plane the fluid is, giving it gravitational potential. Typically the lowest point of a fluid being studied is set to be at zero height, therefore the other locations of the fluid will have a potential energy.
Taken all together, these three terms add up to encompass the fluid’s total energy. Since energy cannot be created or destroyed, while the various terms will be in flux through a studied fluid system, the summed energies will never change.
For Which Flow Can Bernoulli’s Equation Be Applied?
There are several assumptions that need to be made before Bernoulli’s equation may be used to study the flow of a particular fluid. If these simplifications are not assumed, then Bernoulli’s equation cannot take into account everything that is happening as a fluid moves. Here are the requirements necessary to use Bernoulli’s formula:
Fluid Must Travel Along a Streamline
A streamline is the constant (but not necessarily straight) line or path of a fluid, and every curve that is tangent to the velocity vector of the fluid. Essentially this means the fluid must travel in a path that will not change over time. The streamlines will be constant.
Fluid Must Be Inviscid
An inviscid fluid is technically a fluid that has no viscosity. There are very few examples of inviscid fluids in real life, however, hence they are also known as “superfluids” or “perfect fluids”. Because there are almost no practical examples of inviscid fluids that exist naturally, instead flows that can be idealized as laminar are said to be inviscid when using Bernoulli’s equation.
Fluids need to be visualized as inviscid because kinetic energy must be conserved and contribute fully to moving the fluid through a pipe for example, in order to use Bernoulli’s. Viscosity means that a fluid will have frictional losses as it moves through a pipe. With conservation of energy, you would expect the pressure of a fluid to be the same at the start if it goes from a big opening through a small and back to an equally big opening again. However, a viscous fluid will sustain more frictional losses as it moves through the compressed portion of the pipe.
In addition, a viscous fluid is more susceptible to the creation of vortices and eddies that come with turbulent flow. An inviscid fluid is also an irrotational fluid. These results of turbulent flow take kinetic energy away from the direction of the flow vector, and off to paths that are no associated with normal streamlines.
Fluid Must Be in a Steady State
A fluid cannot be studied with Bernoulli’s equation if it changes over time. Note that this does not mean one side of the pipe or tube is different than the other; rather, it means the conditions of the same portion of pipe will change with time. If the velocity were to increase or decrease with time, that would mean the kinetic energy would change and for some period conservation of energy would be broken.
Fluid Must Be Incompressible
An incompressible fluid is one that does not take kinetic or potential energy to expand or compress. While the pressure of the fluid can change, an incompressible fluid will not undergo phase shifts or do work or have work (meaning energy) done to it as it moves. The fluid also maintains a constant density if it is incompressible.
If any of these rules are violated, then so is conservation of energy. For this reason, most gases cannot have Bernoulli’s equation applied, however there are exceptions.
Can Bernoulli’s Equation be Used for Turbulent Flow?
Turbulent flows violate the at least the first three conditions for using Bernoulli’s equation, and the last is violated for turbulent gases. The main reason turbulent flow does not work is because of its random and unpredictable nature. A turbulent fluid does not follow a single, steady streamline, and will change with time as the turbulence unfolds.
Bernoulli’s equation demands that things stay stable and idealized, which is never the case for turbulent flow. Turbulence is viscous flow by nature, as viscosity is required to make the vortices and eddies that form and take kinetic energy away from normal flow. Viscous losses from a turbulent fluid are incompatible with conservation of energy.
Applications of Bernoulli’s Equation
Bernoulli’s equation still has a wide range of use cases when fluids are idealized as laminar and inviscid. While computing frictional losses for systems of pipes and pumps is necessary, Bernoulli’s equation will give a rough approximation of the energy in the system, and how kinetic and mechanical energies shift within.
Perhaps the biggest application of the Bernoulli principle is lift as it relates to airfoils and wings. In a typical airfoil, air moves faster over the top, thus decreasing the pressure above to maintain conservation of energy. With this drop in pressure above, suddenly there is more air pressure beneath the airfoil, and a lift force is generated. Obviously real airplane flight is a bit more complicated than this, but the Bernoulli principle does a good job in explaining the basics of what is going on!
