Turbulent flow is a type of fluid motion characterized by chaotic changes in pressure and flow velocity. It is encountered in various engineering applications, such as fluid flow through pipes, ocean currents, and flow through pumps and turbines.

In this article, we will explore the key features of turbulent flow, including the Reynolds number, factors affecting it, its velocity profile, and its applications in various engineering systems.
Understanding Turbulent Flow
Turbulent flow is a complex fluid motion characterized by chaotic, irregular fluctuations in velocity and pressure. It is encountered in various engineering applications, such as fluid flow through pipes, ocean currents, and flow through pumps and turbines.
In turbulent flow, fluid particles move in an unpredictable manner, with swirling eddies of various sizes interacting and transferring energy across multiple scales, as shown in the diagram below. This contrasts with laminar flow, where fluid particles follow smooth, parallel paths, devoid of swirling motion.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
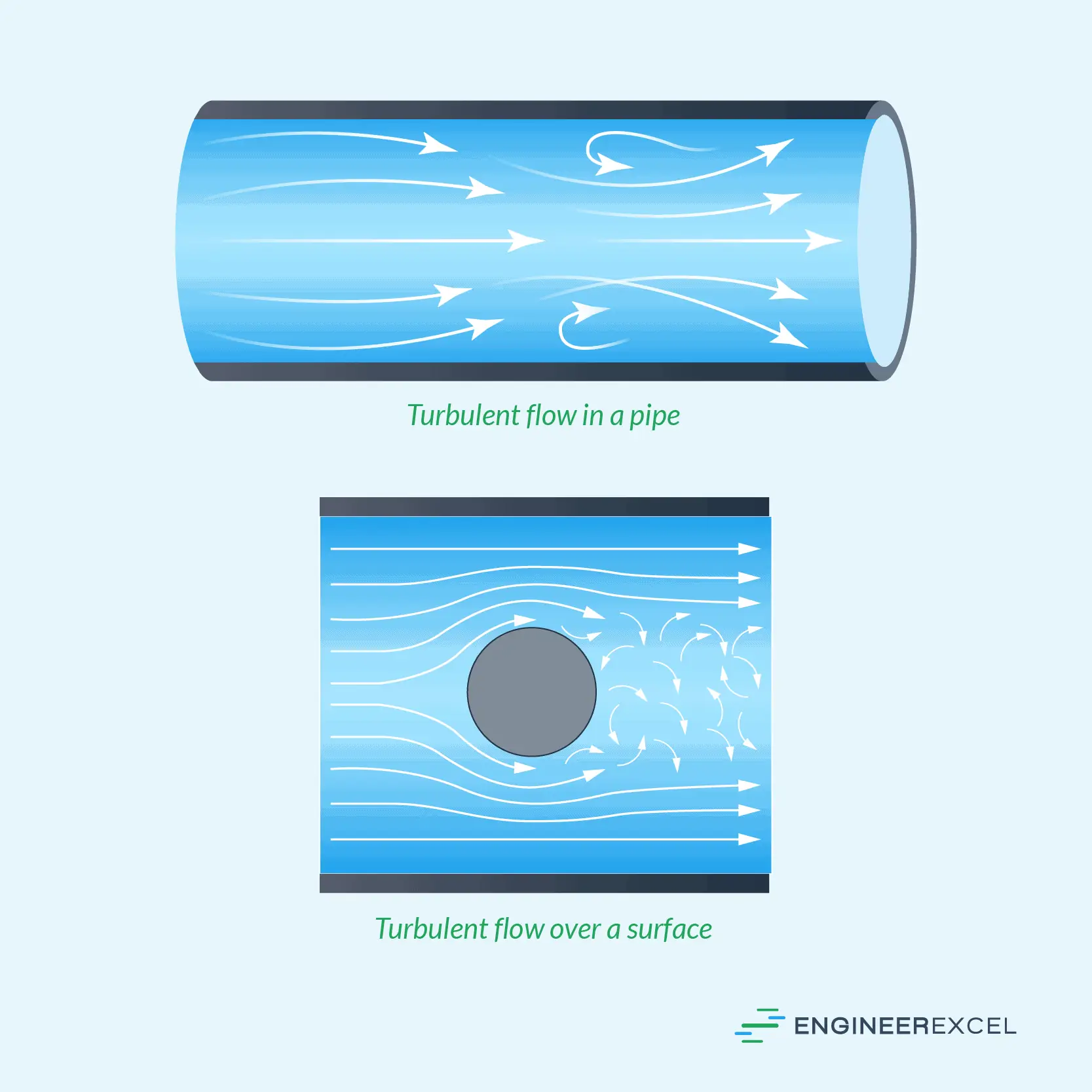
One of the key features of turbulent flow is the presence of a spectrum of eddy sizes, which contribute to the seemingly random motion of the fluid particles. These eddies are generated by the unstable behavior of the fluid and play an important role in the energy cascade process. This process involves the transfer of kinetic energy from the larger, energy-containing eddies down to progressively smaller scales until the energy is eventually dissipated as heat at the smallest, microscale eddies.
Reynolds Number in Turbulent Flow
In fluid dynamics, the Reynolds number (Re) is a dimensionless quantity that captures the relative importance of inertial forces to viscous forces in a fluid flow. It is defined as:
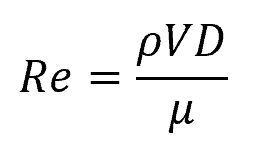
Where:
- ρ = fluid density [kg/m3]
- V = flow velocity [m/s]
- D = characteristic length scale [m]
- μ = fluid dynamic viscosity [Pa-s]
In general, turbulence occurs at high Reynolds numbers. However, the specific Reynolds value at which a flow starts to become fully turbulent varies depending on the geometry of the conduit, surface roughness, and local conditions.
For example, in a smooth, straight pipe, fully turbulent flow typically occurs at Reynolds numbers above 4000. However, this might be lower in pipes with surface irregularities or geometric changes.

In engineering applications, understanding the Reynolds number is essential for predicting and controlling the onset of turbulence in a fluid flow. This is of particular importance because turbulence can significantly affect the performance of various engineering systems, such as increasing drag on aircraft wings or causing pressure loss in pipelines.
Factors Affecting Turbulent Flow
Velocity Gradient
The velocity gradient is a key factor in the development of turbulent flow. A high velocity gradient between fluid layers can lead to increased mixing, causing fluid particles to deviate from their original path, resulting in the formation of eddies. As the velocity gradient increases, so too does the likelihood of turbulence.
Fluid Characteristics
The characteristics of the fluid, such as its density, viscosity, and compressibility, also play a crucial role in the development of turbulent flow. Higher viscosity fluids usually exhibit less turbulence, as the greater internal resistance opposes velocity fluctuations and inhibits the formation of eddies. This can be observed in the formula for the Reynolds number above.
Flow Obstructions
Flow obstructions, such as abrupt changes in duct geometry or the presence of solid objects in the flow path, can also contribute to the development of turbulent flow. These obstructions create pressure drops, causing local variations in fluid velocity and promoting the formation of eddies. Consequently, minimizing the number of valves, turns, and fittings in fluid systems can help reduce turbulence and ensure a smoother flow.
Characterizing Turbulent Flow Velocity Profile
In turbulent flow, the fluid velocity varies in both magnitude and direction. This unpredictable nature of the flow makes it difficult to predict the precise velocity at a given point in space and time. However, the statistical properties and certain spatial features of the turbulent flow can be analyzed and understood.
Characterizing turbulent flow involves understanding various aspects of the flow field, such as mean velocity, turbulent fluctuation, turbulence strength, and turbulence intensity.
Mean Velocity
In turbulent flow, the fluid velocity at a specific point varies with time due to fluctuations caused by turbulent eddies. The mean velocity is the average fluid velocity over a specific period of time. In practice, to calculate the mean velocity, measurements of fluid velocity are typically taken at regular intervals and then averaged, such that:

Where:
- uavg = mean velocity [m/s]
- ui = measured velocities taken at regular intervals [m/s]
- N = number of measured velocities [unitless]
Turbulent Fluctuation
Turbulent fluctuation is the deviation of the fluid velocity from the mean velocity at a particular point in the flow field, as shown in the equation below. These fluctuations are caused by the presence of turbulent eddies of varying sizes, which continually mix the fluid and produce non-uniform velocities.
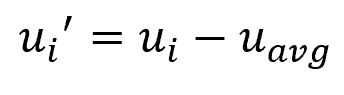
Where:
- ui’ = turbulent fluctuation [m/s]
Turbulence Strength
Turbulence strength, also known as the turbulent kinetic energy, is defined as the root mean square (RMS) of the velocity component’s fluctuations. TKE provides insight into the level of turbulence and energy dissipation occurring within the flow field. It can be calculated using the following formula:
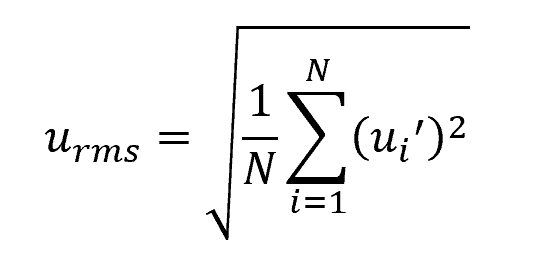
Where:
- urms = turbulence strength [m/s]
Turbulence Intensity
Turbulence intensity is a dimensionless parameter that quantifies the degree of turbulence by dividing the root-mean-square (RMS) of the velocity fluctuations by the mean velocity, as shown in the equation below. High turbulence intensity indicates enhanced energy dissipation and a more chaotic flow, while low turbulence intensity implies a more streamlined and less chaotic flow.

Applications of Turbulent Flow
Turbulent flow plays a significant role in various engineering systems. In the field of combustion, for example, allowing turbulence to occur improves the mixing of fuel and air, enhancing the reaction rate per unit volume of the combustor. This is particularly important for practical devices like internal combustion engines and industrial burners, which rely on turbulence to achieve high efficiency and performance.

This is also utilized in heat exchangers, where higher levels of turbulence result in improved heat transfer rates due to the mixing and dispersion of fluid temperature gradients. Engineers utilize this knowledge to design compact, efficient heat exchangers for systems like power plants and HVAC.
However, in fluid transportation systems, such as pipelines, turbulent flow can cause significant pressure losses due to fluid friction on the pipe walls. Thus, understanding and predicting turbulent flow behavior becomes vital to calculate the required pumping power, minimizing energy consumption, and ensuring the economical operation of fluid transportation networks.
Finally, turbulent flow is relevant in the study of natural phenomena, such as meteorology and oceanography. Meteorologists study turbulence in the atmosphere to better predict weather patterns and air pollutant dispersion, while oceanographers analyze turbulent underwater currents to understand heat transfer processes and nutrient transportation in oceans.
