In fluid dynamics, the term “entrance length” refers to the distance from the entrance of a pipe or channel to the point where the flow has fully developed. In this article, we explain the concept of entrance length, the factors that affect it, and how to calculate it in various flow regimes.
Defining Entrance Length
The velocity and flow profiles within a pipe or conduit are often not fully developed immediately upon entry. Instead, it takes some distance to transition from the initial, often uniform, velocity profile to the fully developed profile. The entrance length quantifies how far this transition occurs.

When a fluid enters a pipe, it experiences friction at the walls, which leads to boundary layer development. The boundary layers from opposite walls continue to grow as the fluid flows through the pipe until they eventually merge. At this juncture, the velocity profile becomes fully developed and remains constant for the rest of the pipe.
Entrance length refers to the distance from the entrance of a pipe or channel, where the fluid first comes into contact with the interior surface, to the point where the flow has fully developed, reaching a steady state of uniform velocity distribution. This is illustrated in the diagram below.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
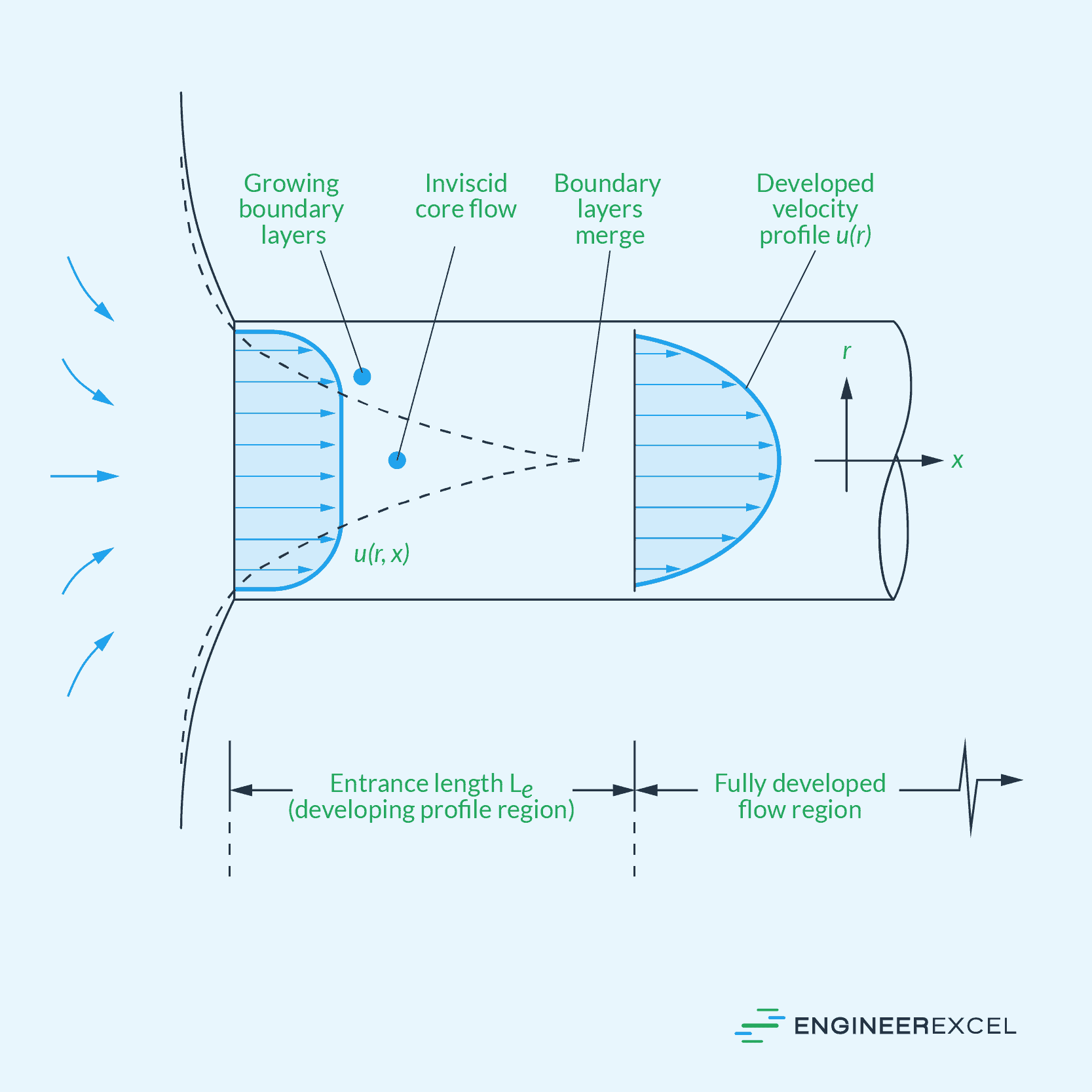
It is important to consider the entrance length when designing pipe systems, as it affects parameters such as pressure drop, fluid velocity, and heat transfer rates. Engineers must ensure that the entrance length is adequate to allow for a fully developed flow in the system, as this ensures accurate predictions of performance and helps avoid potential issues associated with non-uniform flow distribution.
Factors Affecting Entrance Length
The entrance length primarily depends on two parameters: Reynolds number and pipe diameter.
Reynolds Number
The Reynolds number is a dimensionless quantity that indicates the relative importance of inertial and viscous forces in a fluid flow. It can be calculated using the following formula:
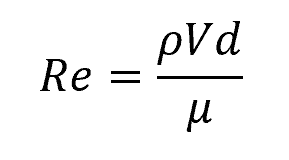
Where:
- Re = Reynolds number [unitless]
- ρ = fluid density [kg/m3]
- V = flow velocity [m/s]
- d = pipe diameter [m]
- μ = dynamic viscosity of the fluid [Pa-s]
The Reynolds number determines the flow regime, which can either be laminar or turbulent. Typically, turbulent flows or higher Reynolds numbers lead to faster growth of boundary layers, resulting in a shorter entrance length. In contrast, laminar flows or lower Reynolds numbers lead to slower grown of boundary layers, resulting in longer entrance length.
Pipe Diameter
Another factor that influences the entrance length is the pipe diameter. In general, a larger diameter results in a longer entrance length, while a smaller diameter shortens it.
Entrance Length Calculation
The formula used for calculating the entrance length depends on whether the flow is laminar or turbulent.
Laminar Flow
In laminar flow, fluid layers move parallel to the pipe walls, and the velocity profile is parabolic. The accepted correlation between the entrance length and Reynolds number in laminar flow is as follows:

Where:
- Le = entrance length [m]
Note that in pipe flows, the flow starts to transition into turbulent when the Reynolds number reaches 2300. Plugging in this value in the equation above, the maximum laminar entrance length possible is given by 138d.
Turbulent Flow
Turbulent flow is characterized by chaotic and irregular fluid motion with significant mixing and eddies. This results in faster growth of boundary layers and shorter entrance length.
There are several empirical formulas that can be used to estimate the entrance length in turbulent flow. For decades, the most widely accepted formula had been the sixth-power-law estimate:
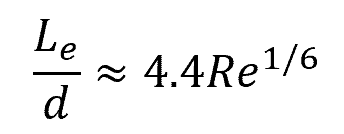
However, recent results by F. Anselmet and S. Dash using computational fluid dynamics suggest a more accurate correlation as follows:
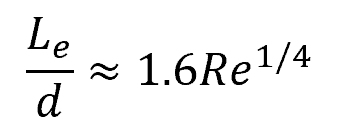
This formula is applicable for Reynolds numbers up to 107. The table below shows the turbulent entrance length estimates at different Reynolds numbers.
| Re | Le/d |
| 4000 | 13 |
| 10^4 | 16 |
| 10^5 | 28 |
| 10^6 | 51 |
| 10^7 | 90 |
Example Problem
Problem Statement: A fluid with a Reynolds number of 500 is flowing through a circular pipe with a diameter of 10 centimeters. What is the estimated entrance length?
Answer: A circular pipe flow with a Reynolds number of 500 is generally considered laminar. Therefore, the entrance length can be estimated using the formula:
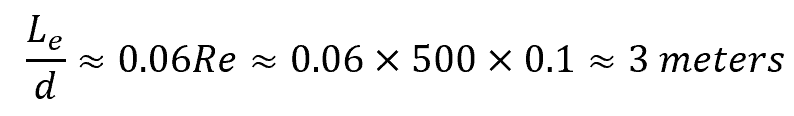
The entrance length is 3 meters.
