Major loss is the energy loss experienced by a fluid due to friction as it flows through a pipe. Understanding this frictional loss is essential for designing efficient pumping and piping systems, as it affects the fluid’s potential energy or head.

In this article, we will discuss major loss, the factors affecting it, and its calculation.
What is Major Loss in Fluid Mechanics
In fluid mechanics, major loss refers to the energy loss experienced by a fluid as it flows through a pipe due to friction. It can be seen as the resistance to flow that the fluid encounters when in contact with the pipe wall. This frictional loss is different from minor losses, which occur due to factors such as changes in section, valves, bends, or other flow disruptions.
As the fluid flows through a pipe, the friction between fluid particles and the pipe wall generates a shear stress, which results in energy loss in the form of heat. This energy loss is generally described as head loss, as it affects the fluid’s potential energy or head.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.

Understanding major loss in fluid mechanics is crucial for designing efficient pumping and piping systems. By accurately estimating the major losses, engineers can optimize system performance, reduce energy consumption, and identify potential issues related to pipe friction. Furthermore, knowledge of major loss will allow for proper sizing of pumps or compressors, thus minimizing operational costs and improving overall system reliability.
Major Loss vs Minor Losses
In contrast to major losses caused by friction, minor losses occur due to changes in the pipe’s flow path, such as bends, valves, fittings, and sudden contractions or expansions. These local disturbances in the flow field result in higher energy losses than expected from friction alone.
Minor losses are typically expressed as a percentage of the kinetic energy of the fluid at the location where the disturbance occurs. To calculate minor losses, loss coefficients are commonly used, which are dimensionless numbers that depend on the specific type of fitting or obstruction.
While major losses are often more significant, especially over long pipe runs, it is crucial not to overlook minor losses as they can substantially affect the overall efficiency of a fluid flow system. In complex pipe systems with multiple bends, fittings, and perhaps different pipe materials, both major and minor losses need to be considered when sizing pumps or evaluating the required pressure head.
Factors Affecting Major Loss
Reynolds Number
Major loss is predominantly influenced by the Reynolds number, which represents the flow regime of a fluid in a pipe. If the Reynolds number is less than 2,300, the flow is considered laminar, which entails smooth fluid motion and relatively low energy loss. In contrast, turbulent flow occurs when the Reynolds number is above 4,000, causing higher energy losses due to chaotic fluid motion and increased friction between the fluid and pipe walls.
Size and Length of Pipe
Another factor greatly impacting major loss is the size and length of the pipe. The pipe diameter has an inverse relationship with major loss, meaning smaller pipes generate higher energy losses due to increased wall friction. On the other hand, the longer the pipe, the more energy is lost as the fluid travels through the pipe, leading to greater heat generation resulting from this friction.
Flow Velocity
Flow velocity is another critical factor that affects major loss in fluid systems. As the flow velocity increases, so does the friction between fluid particles and the pipe walls, leading to higher major losses. Greater velocities can cause a transition from laminar flow to turbulent flow, further increasing energy losses due to the chaotic mixing of fluid particles.
Fluid Properties
Lastly, the properties of the fluid itself, specifically density and viscosity, have significant effects on major loss in fluid mechanics. Fluids with higher density generate greater energy losses due to their larger mass and increased friction with the pipe walls. Additionally, fluids with higher viscosity exhibit greater resistance to flow, which also contributes to the increased energy losses observed in viscous fluid systems.0
Major Loss Calculation
The major loss can be estimated using the Darcy-Weisbach equation:
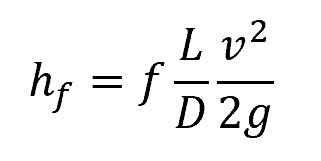
Where:
- hf = major head loss [m]
- f = friction factor [unitless]
- L = pipe length [m]
- D = pipe diameter [m]
- v = flow velocity [m/s]
- g = acceleration due to gravity [9.81 m/s2]
The friction factor is a dimensionless number that quantifies the resistance encountered by the fluid as it flows through the pipe. There are several ways to estimate the friction factor, depending on whether the flow is laminar or turbulent.
In laminar circular pipe flow, the friction factor is only dependent on Reynolds number. It can be calculated using the following formula:
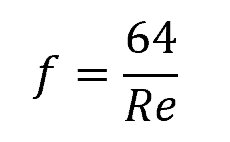
Where:
- Re = Reynolds number [unitless]
For turbulent flow, the friction factor must be determined using empirical correlations or methods, such as the Colebrook-White equation:

Alternatively, it can be approximated using the Moody chart:
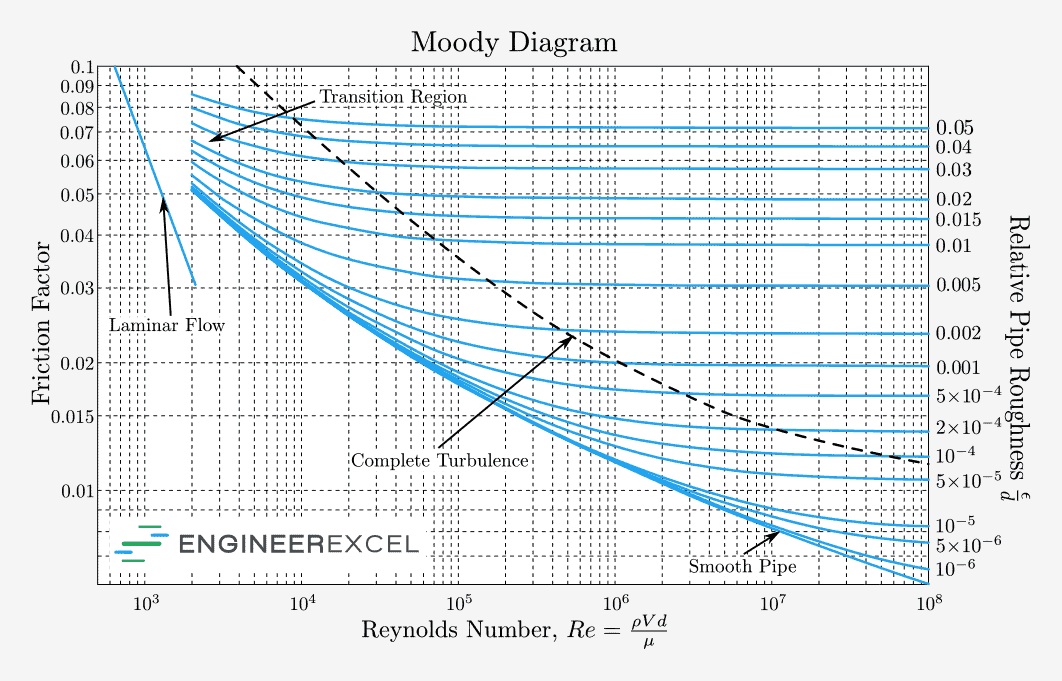
Example Problem
Problem: An oil with a viscosity of 0.10 Pa-s and density of 890 kg/m3 flows through a 10 m long pipe with a diameter of 50 mm at 2.0 m/s. The pipe has a relative roughness of 0.015. Calculate the major loss in the pipe.
Solution:
First, we need to calculate the Reynolds number to determine the flow regime. The Reynolds number formula is:
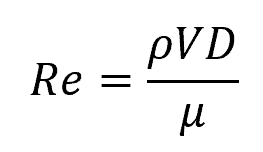
Where:
- ρ = fluid density [kg/m3]
- V = fluid velocity [m/s]
- D = pipe diameter [m]
- μ = fluid viscosity [Pa-s]
Plugging in the values, we get:
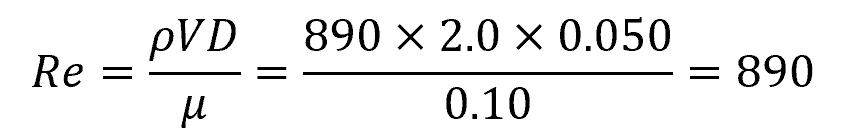
Since the Reynolds number is less than 2300, the flow is laminar. For laminar flow, the friction factor can be calculated using the following formula:
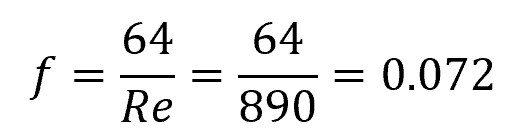
Next, we can calculate the major loss using the Darcy-Weisbach equation, which is:
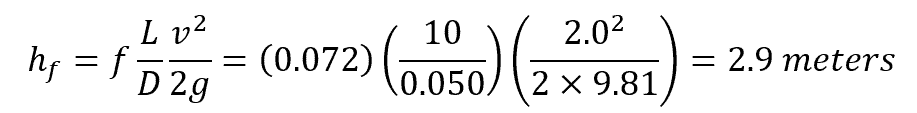
Therefore, the major head loss due to friction is 2.9 meters.
