Critical flow in open channels refers to the state where the specific energy is at a minimum for a particular discharge, indicating the point at which the flow transitions between subcritical and supercritical regimes. It is a key parameter in hydraulic analysis and influences the behavior of the flow, including the formation of standing waves and other hydraulic phenomena.

In this article, we will discuss the concept of critical flow, including the calculation of critical depth for different channel shapes, the significance of Froude number in determining flow regimes, and the implications of critical flow on hydraulic structures and flow patterns.
What is Critical Flow
In an open channel, the total head of energy of the fluid can be mathematically expressed as:


Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Where:
- H = total head of energy [m]
- z = elevation [m]
- y = depth of fluid [m]
- V = flow velocity [m/s]
- g = gravitational acceleration [9.81 m/s2]
The mechanical portion of this total head is called the specific energy:

Where:
- E = specific energy [m]
- Q = flow rate [m3/s]
- A = cross-sectional area of the flow [m2]
The specific energy can be interpreted as the energy per unit weight relative to the bottom of the channel. In line with this, the critical flow of an open channel is defined as the state where the specific energy is at a minimum for a particular discharge.
To illustrate, we can plot the specific energy with respect to the depth of fluid, as shown in the diagram below.

In the diagram above, the critical flow happens at the point (Emin, yc), where Emin is the minimum specific energy and yc is the critical depth at which the critical flow occurs.
It is important to know the critical depth of open channels because it is a key parameter in hydraulic analysis. Critical depth serves as a control point when the flow changes from subcritical to supercritical, and it influences the behavior of the flow, including the formation of standing waves and other hydraulic phenomena.
Critical Depth Calculation
In order to find the point of minimum specific energy, we can equate the derivative of the above equation to zero. This results to the following equation:
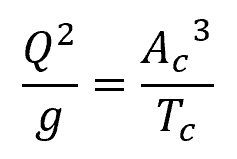
Where:
- Ac = cross-sectional flow area at critical flow conditions [m2]
- Tc = width of the channel section at the free surface at critical flow [m]
The relationship between Ac, Tc, and yc depends on the shape of the channel. Once the critical depth is found, the minimum specific energy at this depth can be calculated using the following equation:
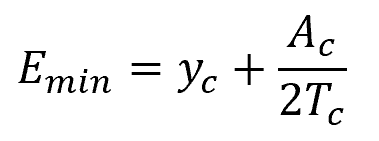
Where:
- Emin = minimum specific energy [m]
Critical Depth for Rectangular Channel
For example, for a rectangular channel, the above equation can be transformed to get the critical depth as follows:
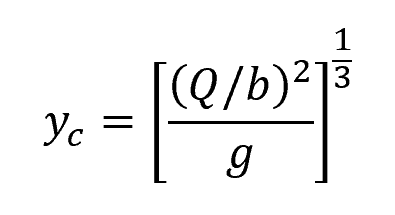
Where:
- b = width of the channel [m]
In this case, the critical width of the channel section at the free surface, Tc, is also equal to b. Furthermore, the minimum specific energy can be calculated from the critical depth as follows:

Critical Depth for Triangular Channel

For a triangular channel, the critical depth can be calculated using the following equation:

Where:
- m = slope of the triangular channel bed [unitless]
It follows that the critical width of the channel section at the free surface is equal to:
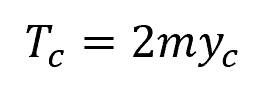
Furthermore, the minimum specific energy can be calculated from the critical depth as follows:

Critical Depth for Circular Channel
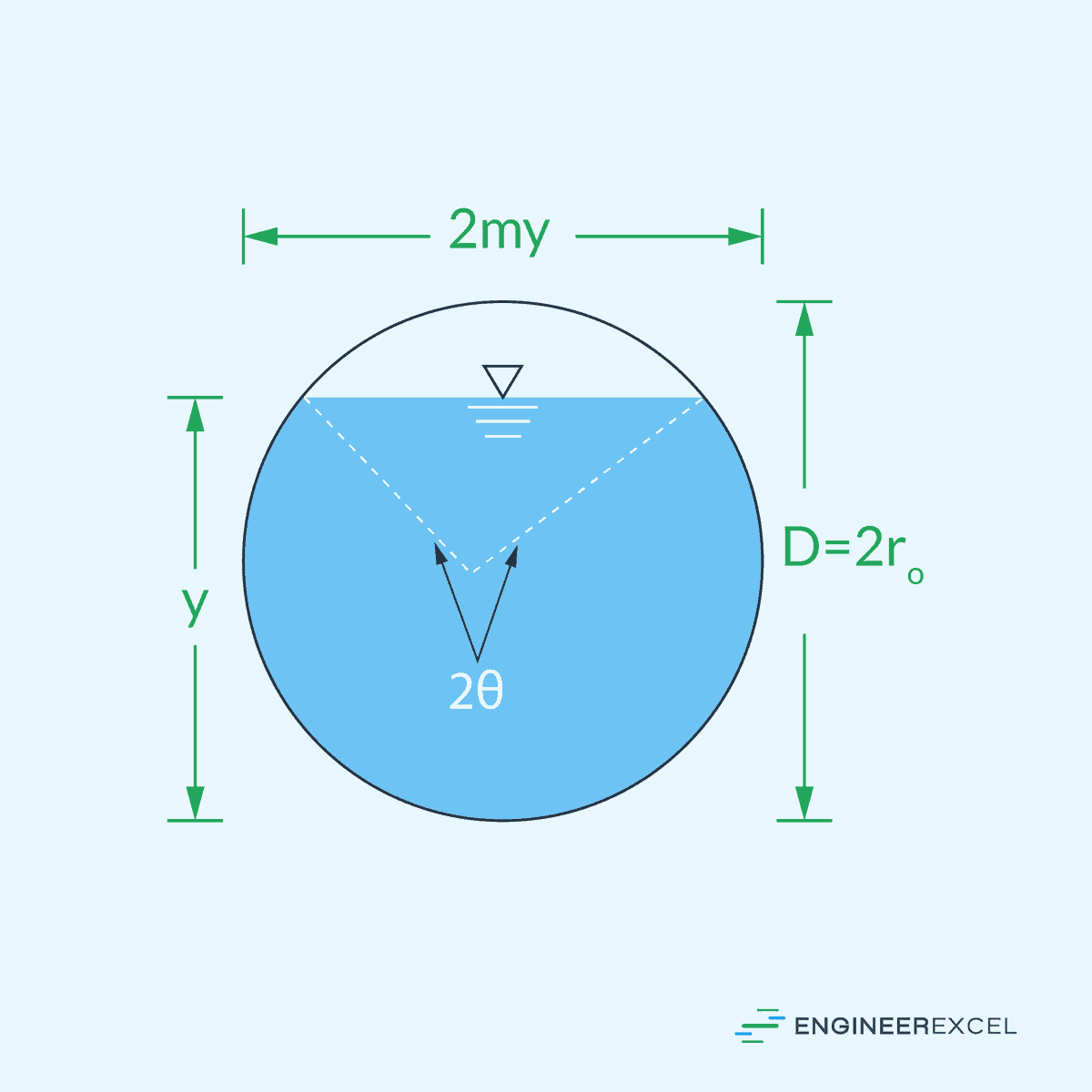
For a circular open channel, critical flow occurs at the following condition:
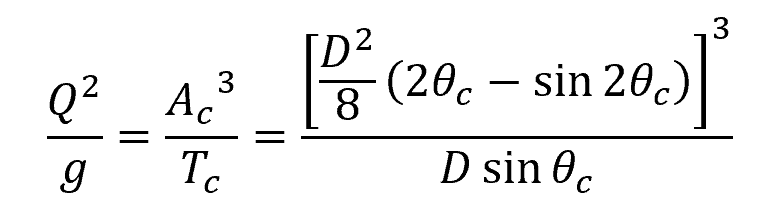
Where:
- 2θc = critical angle subtended by the water surface [rad]
- D = diameter of the circular channel [m]
Once the critical angle is found, the critical depth can be calculated using the following formula:
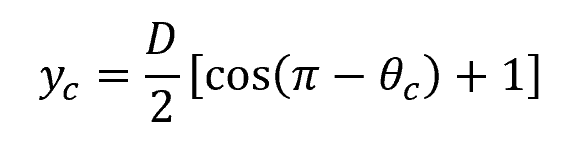
And the critical width of the channel section at the free surface is equal to:
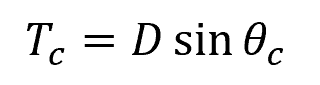
Froude Number for Critical Flow
Critical flow in open channels is a state in which the water flow’s velocity is equivalent to the speed at which disturbances of the free surface move through shallow water. This condition arises when the Froude number, a dimensionless parameter representing the balance between inertial and gravitational forces within the channel, is equal to 1.
The Froude number can be mathematically expressed as:
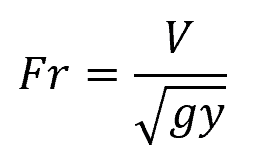
Where:
- Fr = Froude number [unitless]
A Froude number less than 1 indicates subcritical flow, in which gravitational forces are dominant. This flow regime can be characterized by slower velocities and larger depths.
A Froude number greater than 1 represents supercritical flow, where inertial forces dominate, leading to rapid velocities and shallow depths.
A Froude number equal to 1 corresponds to critical flow, the point at which the flow transitions between subcritical and supercritical regimes.
A channel reaches critical flow when the water’s velocity is in equilibrium with external forces. In this state, any perturbations on the water surface propagate neither upstream nor downstream.
Understanding the Froude number and flow regimes is essential for an accurate analysis of open channel flow, as well as designing effective hydraulic structures such as weirs, spillways, and chutes. The flow regime dictates the stable patterns that can occur in an open channel and influences the formation of hydraulic jumps, energy dissipations, and sediment transport.
Example Problem
Problem: A rectangular open channel has a width (b) of 4 meters and a bottom slope of 0.001. The channel carries a discharge of 10 cubic meters per second. Calculate the critical depth and the minimum specific energy at critical flow conditions in the channel.
Solution: The critical depth of a rectangular channel can be calculated as follows:
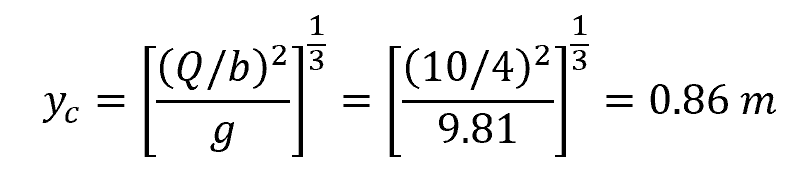
Then, we can calculate the minimum specific energy using the following relation:
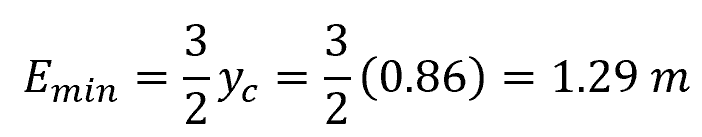
Therefore, the critical depth of flow in the rectangular open channel is approximately 0.86 m and the corresponding minimum specific energy at critical flow conditions is 1.29 m.
