Transitional flow is the fluid flow regime that occurs between laminar and turbulent flow. In this regime, the flow switches randomly between laminar and turbulent states, making it difficult to predict and control.

In this article, we discuss the characteristics of transitional flow, the Reynolds number range in which it occurs, the factors influencing it, and numerical simulations used to gain a deeper understanding of its behavior.
What is Transitional Flow
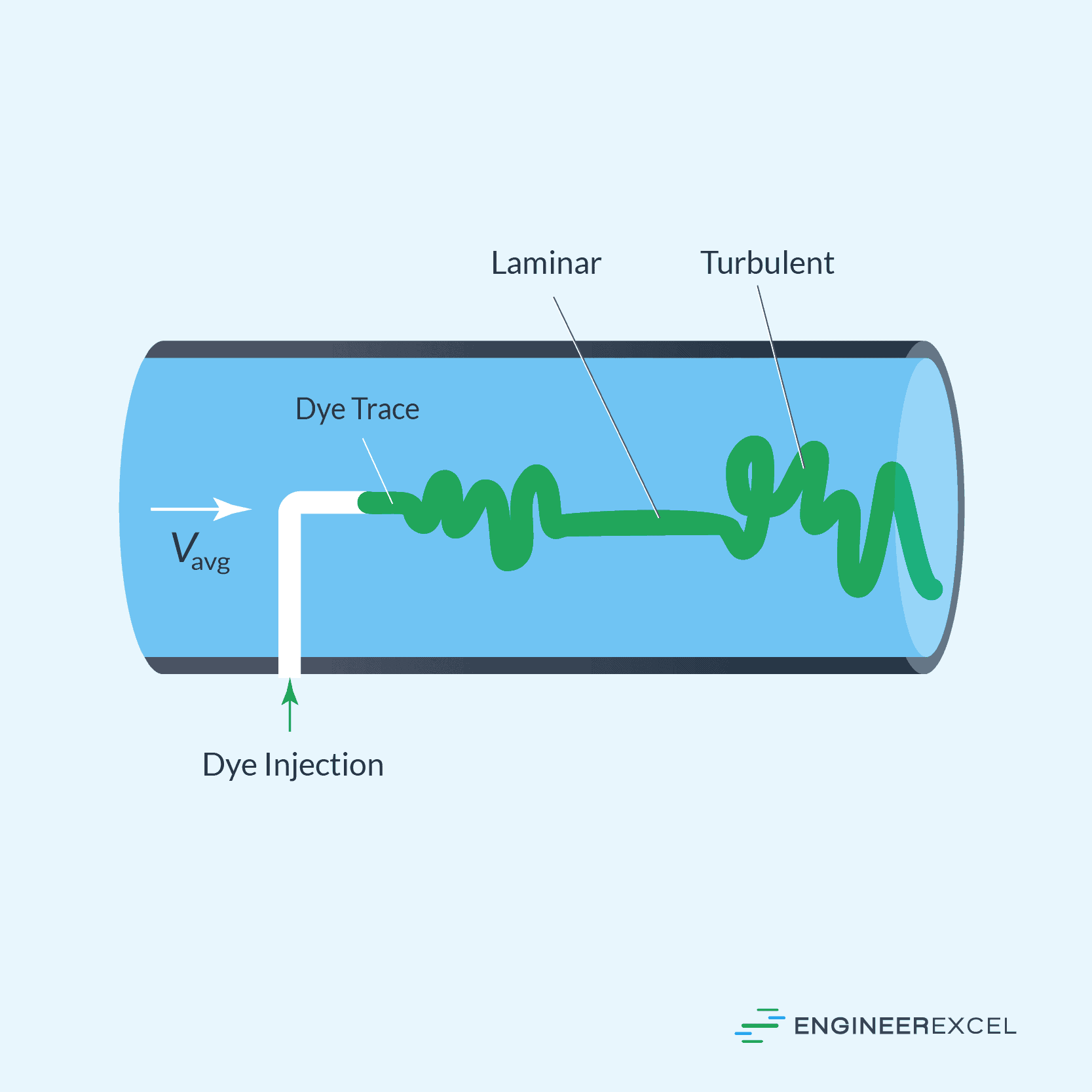
Transitional flow is a fluid flow regime that occurs between laminar and turbulent flow. In this regime, the flow switches between laminar and turbulent states randomly. The diagram below shows the behavior of colored fluid injected into a transitional flow in a pipe.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
It is essential to understand the characteristics of transitional flow in fluid mechanics, as it plays a significant role in various engineering applications. However, it is generally not advisable to design flow operations in the transition region, as the flow behavior can be challenging to predict and control.
In the transitional flow regime, the fluid exhibits both laminar and turbulent characteristics. The flow may appear to be laminar in certain regions, while localized pockets of turbulent flow may be present simultaneously.
This mixed behavior results from fluctuations in the fluid’s velocity and the interaction between its molecules. Fluid particles near the boundary layer experience less resistance and tend to move in a stable, laminar fashion, whereas particles away from the boundary layer experience more resistance, leading to the development of turbulent flow.
Reynolds Number in Transitional Flow
Transitional flow is observed in a narrow range of Reynolds numbers, typically between 10^3 and 10^4. The Reynolds number (Re) is a dimensionless quantity used to categorize fluid flow patterns and determine the flow regime. It is calculated as:
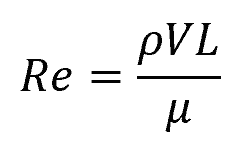
Where:
- Re = Reynolds number [unitless]
- ρ = fluid density [kg/m3]
- V = mean flow velocity [m/s]
- L = characteristic length [m]
- μ = fluid’s dynamic viscosity [Pa-s]
The specific values of Reynolds number at which transitional flow occurs depends on factors such as flow geometry, surface roughness, and fluctuations in the inlet stream. In circular pipe flow, this flow regime usually takes place when the Reynolds number is between 2300 and 4000.
Factors Influencing Transitional Flow
Fluid Properties
Fluid properties are the primary factors that influence transitional flow. Fluids with higher viscosity, for example, are more resistant to flow disturbances and may exhibit a more extended region of transitional flow. Conversely, fluids with lower viscosity may experience a quicker transition to turbulent flow due to their susceptibility to disturbances.
Surface Roughness
Surface roughness plays a significant role in determining the onset of transitional flow. Rough surfaces tend to disturb flow lines, creating localized regions of turbulence.
However, surface roughness also impacts the transition of flow through a reduction in shear stress, which can help delay the onset of turbulence. An increase in surface roughness can cause flow conditions to change from laminar to turbulent in a relatively fast manner, while smoother surfaces allow for a more gradual transition.
External Factors
External factors, such as pressure fluctuations, flow disturbances, and vibrations, can also impact transitional flow characteristics. Pressure fluctuations can lead to an oscillation between laminar and turbulent flow regions, while flow disturbances and vibrations can create local turbulence, affecting the overall flow behavior.
Numerical Simulations of Transitional Flow
Transitional flow is the most complex and unpredictable among the flow regimes. To gain a deeper understanding of the underlying physics behind the behavior of transitional flow, numerical simulations are widely used. There are two popular techniques employed in numerical simulations of transitional flow: Direct Numerical Simulation (DNS) and Large Eddy Simulation (LES).
Direct Numerical Simulation
Direct Numerical Simulation (DNS) is a computation-intensive approach that aims to resolve all the scales of turbulence by solving the full Navier-Stokes equations. It provides a detailed and accurate representation of the fluid motion by capturing every turbulent eddy and interaction without any modeling approximations. However, the tremendous computational resources required make DNS suitable only for relatively low Reynolds number cases or small-scale problems.
Despite its high computational demands, DNS has contributed significantly to our understanding of turbulent flow physics and provided valuable data for developing and validating turbulence models.
Large Eddy Simulation
Large Eddy Simulation (LES) is a more practical and computationally efficient approach compared to DNS. It resolves the large-scale turbulent eddies directly while modeling the smaller, unresolved scales that are more universal and less dependent on the flow geometry. This selective resolution allows LES to capture the most significant features of transitional flows while reducing the computational requirements substantially.
However, LES is still a relatively expensive method and might not be feasible for all flow problems. Additionally, the accuracy of LES is heavily reliant on the quality of the sub-grid scale models used.
