A hydraulic jump is a rapid change in water flow typically observed in open channels, characterized by the transition from a supercritical flow (higher velocity) to a subcritical flow (lower velocity). This abrupt change causes energy dissipation and turbulence, resulting in a distinct jump-like feature in the water surface.

In this article, we will discuss the formation of hydraulic jumps, including their classifications based on the upstream Froude number, calculations related to hydraulic jumps, and their engineering and environmental applications.
What is a Hydraulic Jump?
A hydraulic jump is a sudden transition from a high-velocity, low-depth flow to a low-velocity, high-depth flow, typically occurring in open channels and rivers. This phenomenon occurs when a fast, low-depth flow encounters a more resistant flow, leading to an abrupt change in flow depth and energy dissipation. Hydraulic jumps are relevant to the fields of civil and environmental engineering, as they are commonly observed in structures such as weirs, spillways, and dam releases.
The main factor contributing to the occurrence of a hydraulic jump is the Froude number. The Froude number is a dimensionless quantity that characterizes the flow regime:

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
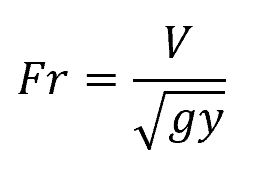
Where:
- Fr = Froude number [unitless]
- V = flow velocity [m/s]
- g = acceleration due to gravity [9.81 m/s2]
- y = flow depth [m]
A hydraulic jump occurs when there is a sudden change in the flow regime from supercritical (Fr>1) to subcritical flow (Fr < 1). In other words, it occurs when the flow velocity decreases to less than the speed of the gravity wave.

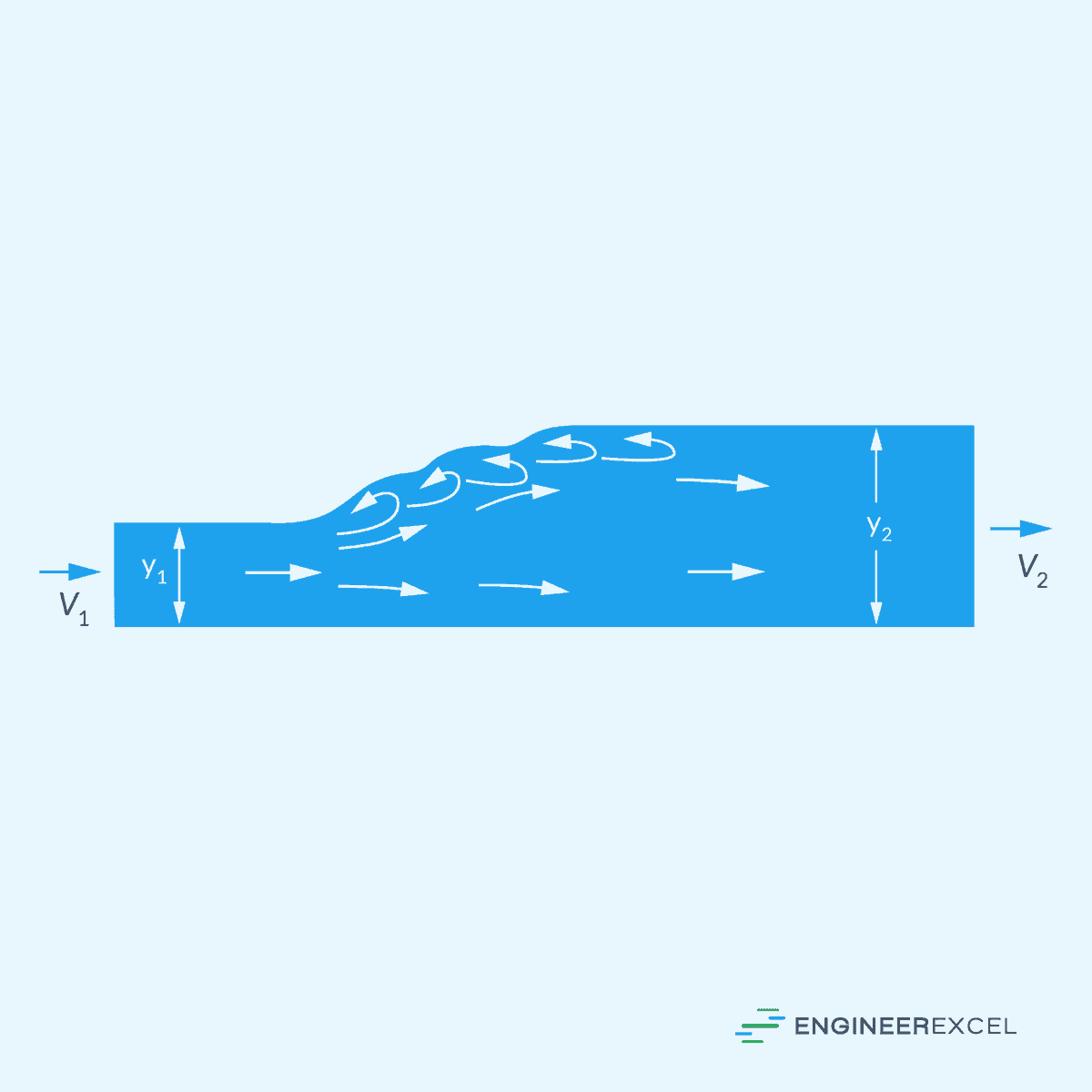
To give an example, the diagram above shows a subcritical flow upstream of the sluice gate. As the flow area changes, it then accelerates to critical and supercritical flow as it passes under the gate. However, further downstream, the flow returns back to subcritical because the downstream “receiver” height is too high to maintain supercritical flow.
This transition from supercritical to subcritical is known as a hydraulic jump. As depicted in the diagram above, the flow passes through the critical depth, which is equal to:
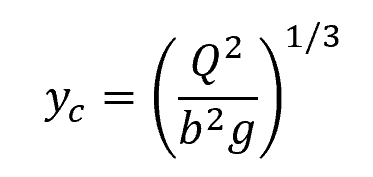
Where:
- yc = critical depth [m]
- Q = flow rate [m3/s]
- b = width of the flow channel [m]
In general, hydraulic jumps range in length from 4 to 6 times the downstream depth.
Hydraulic Jump Classifications
The performance of hydraulic jumps can be primarily classified based on the upstream Froude number (Fr1)— the Reynolds number and channel geometry have only a secondary effect. Each group corresponds to specific characteristics and energy dissipation percentages. Understanding these categories is important for determining the best design range and jump performance, as well as avoiding potential hazards to banks and structures downstream.
≤ Fr1 ≤ 1.7
A Froude number ranging between 1.0 and 1.7 corresponds to a standing-wave or undular jump, which is characterized by low energy dissipation of less than 5%. Jumps in this category exhibit a wave pattern about 4 times the downstream depth (y2) in length.

1.7 < Fr1 ≤ 2.5
For Fr1 values between 1.7 and 2.5, the jump involves a smooth surface rise with small rollers, often referred to as a weak jump. This type of jump dissipates energy ranging from 5% to 15%.
2.5 < Fr1 ≤ 4.5
When the Froude number is within the range of 2.5 to 4.5, the jump becomes unstable and oscillating. This leads to the formation of large waves that may travel downstream for miles, potentially causing damage to earth banks and nearby structures. Such jumps are not recommended for design conditions and exhibit energy dissipation between 15% and 45%.

4.5 < Fr1 ≤ 9.0
The most desirable hydraulic jump occurs when the Froude number is within the range of 4.5 to 9.0. In this case, the jump is stable, well-balanced, and steady, providing the best performance and action. Moreover, these jumps are insensitive to downstream conditions, making them ideal for design purposes.
The observed energy dissipation falls between 45% and 70%.

Fr1 > 9.0
Lastly, jumps with Froude numbers greater than 9.0 are characterized as rough, somewhat intermittent strong jumps. These jumps have good performance, although they are not as optimal as those with a Froude number between 4.5 and 9.0. Rough jumps dissipate energy in the range of 70% to 85%.

It is important to note that when the upstream Froude number is less than 1.0, a hydraulic jump is deemed impossible, as it violates the second law of thermodynamics.
Furthermore, the specifics of jump formation and properties vary depending on the shape of the channel and flow conditions. For instance, the hydraulic jump in a rectangular channel has different characteristics compared to the jump in a circular one. Other factors influencing jump formation include approach flow velocity, channel slope, channel roughness, and downstream control structures.
Hydraulic Jump Calculations
When the initial flow conditions and channel geometry are known, various jump parameters can be determined using conservation formulas and the hydraulic jump relations that account for the momentum and energy transfers.
Change in Depth
In a hydraulic jump, the depth of flow transitions from a high-velocity, low-depth (supercritical) state to a low-velocity, high-depth (subcritical) state. To calculate the change in depth, we can use the following equation:
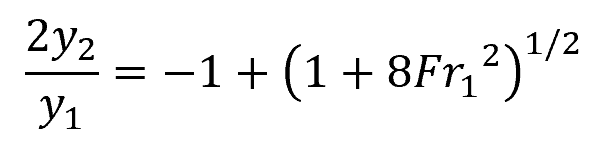
Where:
- y1 = initial depth [m]
- y2 = final depth [m]
- Fr1 = Froude number before the jump [unitless]
Change in Velocity
Once the initial and final depths are known, the change in velocity can be calculated using continuity relation:
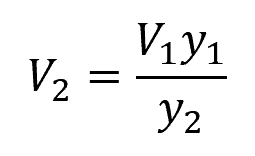
Where:
- V1 = initial flow velocity [m/s]
- V2 = final flow velocity [m/s]
Energy Loss
Energy loss in a hydraulic jump occurs due to turbulence and mixing. To calculate the dissipation head loss across the jump, the following equation can be used:
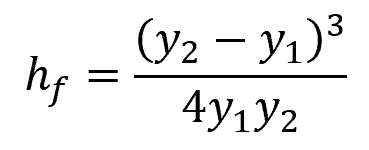
Where:
- hf = dissipation head loss [m]
Applications of Hydraulic Jumps
Hydraulic jumps have several practical applications in engineering and environmental contexts. One is energy dissipation.
Hydraulic jumps are commonly implemented in dam designs to dissipate the excess kinetic energy of the water flow downstream of spillways, thereby reducing the erosive forces acting on the riverbed and banks. This helps prevent excessive scouring that can lead to structural failures or sedimentation issues in downstream areas. Engineers typically use various types of energy dissipators, such as stilling basins, impact basins, or plunging jets to create controlled hydraulic jumps.
Hydraulic jumps also play an important role in flood control structures such as stormwater management ponds and weirs. By creating hydraulic jumps, engineers can effectively slow down the flow of water during heavy rainfall events, allowing for better sedimentation and containment of pollutants. Moreover, controlled hydraulic jumps help mitigate the risk of flooding in urban areas by reducing the peak flow rates downstream.

In sewage and wastewater treatment plants, hydraulic jumps assist in the aeration and mixing of the water. The turbulence created by the hydraulic jump promotes oxygen transfer, facilitating the breakdown of organic matter by aerobic bacteria. The jump also helps in the settling and removal of suspended solids, contributing to the overall efficiency of the treatment process.
Lastly, hydraulic jumps can be employed as part of river training strategies to manage the river’s course, minimize erosion, and preserve the integrity of channel boundaries. Structures like drop structures, chute spillways, and gabions can be designed to produce controlled hydraulic jumps, thus localizing the energy dissipation and preventing excessive excavation of the riverbed.
