Couette flow and Poiseuille flow are two fundamental flow concepts often encountered in fluid mechanics. Couette flow refers to the laminar flow induced by the relative motion between two parallel surfaces, such as the flow of fluid between two flat plates. Poiseuille flow, on the other hand, describes the steady, incompressible flow of fluids through a cylindrical pipe or channel with uniform cross-section.

Overview of Couette Flow
Couette flow occurs when a fluid is trapped between two parallel surfaces moving relative to each other. You may encounter this type of flow when examining the motion of fluids in a journal bearings or a rheometer.
For an incompressible fluid, Couette flow is characterized by a constant velocity gradient in the direction perpendicular to the parallel surfaces. This can result in the fluid having a linear velocity profile.


Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Shear stress in the fluid is directly proportional to the fluid’s dynamic viscosity and velocity gradient. In applications like rheometers, this property can be used to determine a fluid’s viscosity.
Another important aspect of Couette flow is that the pressure gradient in the flow direction is typically negligible, especially at low Reynolds numbers. This results in the flow being primarily driven by the motion of the surfaces and not by any external pressure forces. Under these conditions, the flow can be considered a balance between viscous forces and the surface-driven shear forces.
Couette flow can also exhibit a range of behaviors depending on the Reynolds number. At low Reynolds numbers, the flow is generally laminar and stable, while at higher Reynolds numbers, it can transition to turbulent flow or exhibit instabilities.
Basics of Poiseuille Flow
Poiseuille flow refers to the steady-state laminar flow of an incompressible, viscous fluid in a cylindrical pipe or tube of constant cross-section. It is named after Jean Leonard Marie Poiseuille, who first derived the governing equations in the mid-19th century.
The driving force for Poiseuille flow is a constant pressure gradient along the pipe. The fluid moves due to the balance between the pressure gradient and the viscous resistance. An important feature of this flow is that fully developed Poiseuille flow is independent of the axial coordinate, implying that the flow field is invariant along the pipe.
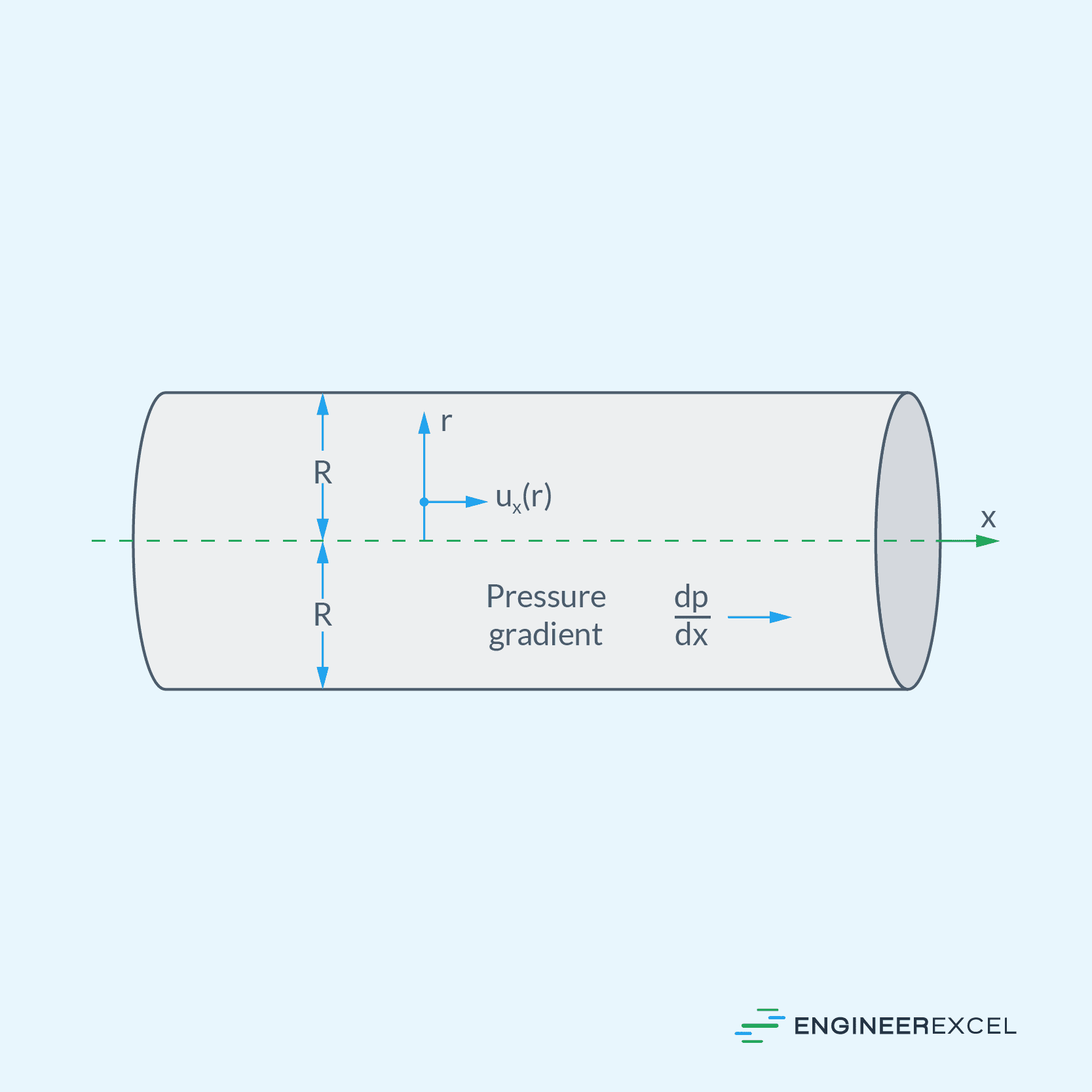
To describe Poiseuille flow quantitatively, you can apply the Navier-Stokes equations and the continuity equation to the fluid motion within the cylindrical pipe. After making several simplifications, including the assumption of fully developed flow, a second-order, linear ordinary differential equation is obtained. The solution of this equation yields the well-known parabolic velocity profile, where the fluid velocity is maximum at the center of the pipe and decreases to zero at the pipe walls.
In engineering applications, Poiseuille flow is commonly used in microchannels and capillary tubes, as well as in some medical procedures such as blood flow in small vessels. It is also applicable to the flow of lubricating oils between moving machine parts and the transport of fluids in porous media. Understanding Poiseuille flow aids in predicting fluid velocity and calculating pressure loss in these various systems.
Couette Flow vs Poiseuille Flow
While Couette flow and Poiseuille share some similarities, they also exhibit distinct characteristics.
Couette flow occurs when a fluid is sheared between two parallel surfaces moving relative to each other. The fluid motion is caused by the shearing forces that exist between the fluid layers and the parallel surfaces. In this flow, the pressure gradient is negligible, and the flow profile depends on the relative speed of the surfaces.
In contrast, Poiseuille flow refers to the laminar flow of a viscous fluid through a cylindrical pipe or a channel with a constant cross-sectional area. The fluid motion is driven by the pressure gradient across the pipe or channel. The flow profile in Poiseuille flow is parabolic with a peak at the center of the pipe and zero velocity at the walls.
The table below summarizes the differences between Couette Flow and Poiseuille Flow.
| Couette Flow | Poiseuille Flow | |
|---|---|---|
| Driving Mechanism | Shearing forces (no pressure gradient) | Pressure gradient (along the pipe) |
| Fluid Motion | Parallel to the walls | Axial (along the pipe) |
| Velocity profile | Linear | Parabolic (peak at the center) |
| Wall shear stress | Constant | Varies with radial distance |
| Dependency on viscosity | Directly proportional | Inversely proportional |
In practical applications, the choice between Couette and Poiseuille flow models depends on the specific problem requirements. For instance, you might use Couette flow to analyze lubrication systems where shearing forces dominate, while Poiseuille’s flow is more suited for the study of blood flow through blood vessels, or fluid flow through pipes, and channels in microfluidic devices.
Bear in mind that these are idealized models of fluid flow, and real-life applications often involve a combination of both Couette and Poiseuille flow, sometimes with additional factors such as turbulence.
