Fluids flowing over flat surfaces hold significant importance in various practical applications, such as plate heat exchangers and aerodynamic vehicle design. One of the fundamental parameters used for analyzing this behavior is the Reynolds number.

This article tackles the Reynolds number, particularly in the context of laminar flow over flat plates.
Reynolds Number for Laminar Flow Over Flat Plate
The Reynolds number is a dimensionless parameter used to predict the flow regime of a fluid. It essentially indicates whether the flow will be laminar, turbulent, or somewhere in between.
In laminar flow, the fluid moves smoothly and predictably, with parallel layers sliding past each other. This is in contrast to turbulent flow, where the fluid exhibits chaotic and irregular behavior, characterized by swirling eddies and vortices.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
When fluid flows laminarly over a flat plate, the fluid particles in direct contact with the surface stick to the plate, following the no-slip condition. This means that the fluid layer adjacent to the plate has zero relative velocity with respect to the plate.
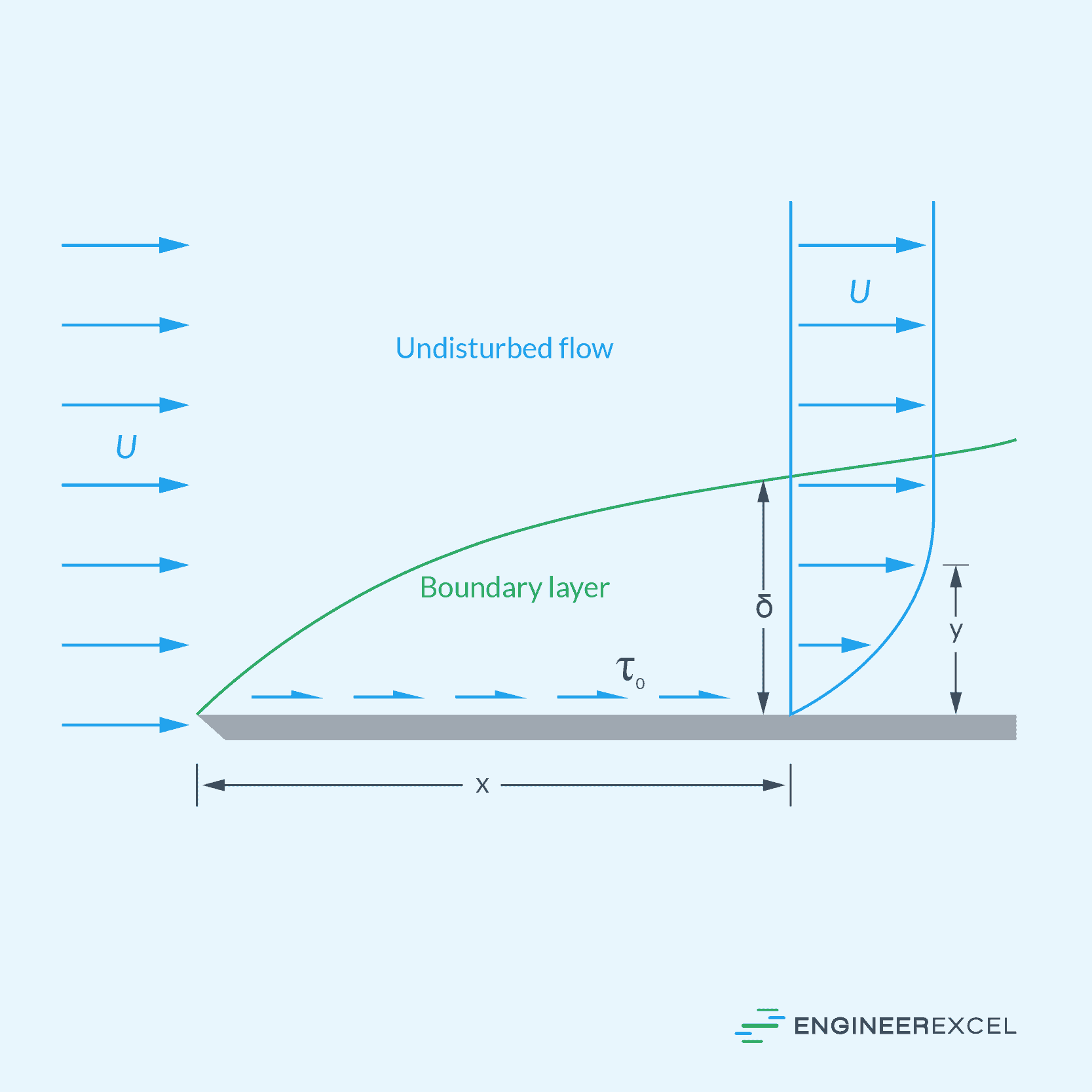
Due to the fluid’s viscosity, a region known as the boundary layer forms adjacent to the surface. In this boundary layer, the fluid’s velocity experiences a rapid transition from zero at the surface to its maximum velocity in the free stream. In general, the velocity profile of laminar flow is parabolic in nature.
As shown in the diagram below, the thickness of this boundary layer progressively increases as the fluid flows across the surface from the leading edge of the plate.
For such flow, the local Reynolds number with respect to the distance from the leading edge of the plate can be calculated using the following formula:
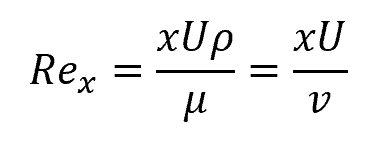
Where:
- Rex = local Reynolds number [unitless]
- x = distance from the leading edge of the plate [m]
- U = free-stream fluid velocity [m/s]
- ρ = density of the fluid [kg/m3]
- μ = dynamic viscosity [N-s/m2]
- v = kinematic viscosity [m2/s]
As shown in the equation above, the higher the viscosity of the fluid, the lower the Reynolds number. Conversely, the higher the fluid velocity, the higher the Reynolds number.
Additionally, as fluid moves across the plate, any molecular disturbances in the flow become more pronounced, leading to an increase in the Reynolds number. After traveling a certain distance, assuming the flow remains uninterrupted by external forces, it will transition from laminar to turbulent when the Reynolds number reaches a critical value, typically around 5×105.
However, it is important to note that the actual value of this critical Reynolds number may vary between 105 and 106, depending on factors like surface roughness, pressure variation along the surface, and the flow conditions in the free-stream region.
Effect of Reynolds Number on Boundary Layer
The Reynolds number has a direct impact on the formation of the boundary layer, particularly on its thickness. The thickness of the boundary layer is defined as the distance from the plate to the point where fluid velocity reaches 99% of the free-stream velocity. As illustrated in the diagram above, it starts thin at the entrance and gradually thickens as it progresses along the plate.
For laminar flow over a flat plate, the boundary layer thickness can be calculated using the following formula:
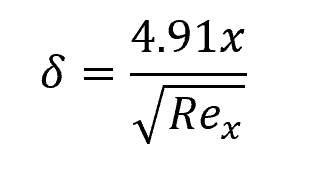
Where:
- δ = thickness of the boundary layer [m]
As per the equation, higher Reynolds numbers result in thinner boundary layers, and conversely, lower Reynolds numbers lead to thicker boundary layers. This explains why turbulent flows exhibit thinner boundary layers compared to laminar flows.
Effect of Reynolds Number on Shear Stress
The Reynolds number also affects the shear stress experienced by the fluid layer adjacent to the plate. For laminar flow over a flat plate, this can be calculated using the following formula:
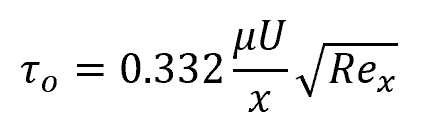
Where:
- τo = shear stress at the plate [Pa]
Effect of Reynolds Number on Friction Coefficient
In line with the shear stress, the Reynolds number also affects the value of the friction coefficient between the fluid and the plate.
The friction coefficient is a dimensionless quantity that measures the skin friction between a fluid and a solid surface over which the fluid is flowing. It is a crucial parameter in determining the drag force that the fluid exerts on the solid surface.

For laminar flow over a flat plate, the local friction coefficient can be calculated using the following formula:

Where:
- cf = local friction coefficient [unitless]
Integrating the local friction coefficient over the entire surface, the formula for the average friction coefficient for laminar flow over a flat plate becomes:

Where:
- Cf = average friction coefficient [unitless]
- Re = Reynolds number based on the whole length of the plate [unitless]
