Bending stress is a type of mechanical stress that occurs when a bending load is applied to a beam, causing it to bend or flex. It results from tension on one side and compression on the other side of the beam.
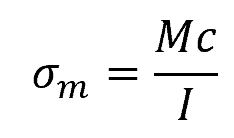
In this article, we will discuss the Bending Stress Formula, which is used to calculate the normal bending stress of a beam under symmetric bending.
What is Bending Stress
Bending stress, which is also referred to as flexural stress, is a mechanical stress that arises when an object is exposed to a bending or flexural load. This type of stress mainly affects structural components such as beams and bridges that are intended to support loads and distribute them over a span. When a material is subjected to a load that causes it to bend or curve, it experiences compression stress on one side and tensile stress on the other side, as shown in the diagram below.

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Bending stress is not uniformly distributed across the cross-section of an element. Its intensity varies from zero at the neutral axis to a maximum value at extreme fibers.
For homogeneous isotropic materials under linear elastic deformation, the distribution of the normal bending stress is linear. However, if the elastic limit is exceeded or the material is non-homogeneous, the normal stress distribution becomes non-linear.
It is worth mentioning that excessive bending stress can lead to structural failure in the form of cracking, deformation, or even rupture. Therefore, understanding and accurately predicting bending stress is paramount for engineers and designers to ensure the safety and longevity of structures.
Bending Stress Formula
The formula used to calculate the normal bending stress in a straight member with a cross section that is symmetrical to an axis is known as the Bending Stress Formula or the Flexure Formula. This is given by the following equation:
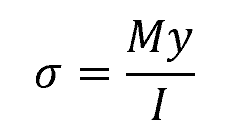
Where:
- σ = normal stress due to bending [Pa]
- M = applied bending moment [N-m]
- y = distance from the neutral axis to the point at which the stress is being calculated [m]
- I = moment of inertia [m4]
This formula only applies when the moment is applied along the neutral axis and perpendicular to the axis of symmetry. Moreover, although this formula assumes that the member is prismatic, we can in most cases of engineering design also use the flexure formula to approximate the normal stress in members that have a slight taper.
Using the same formula, the maximum normal stress due to bending experienced at the outermost fiber of a cross-section can be determined to be equal to:
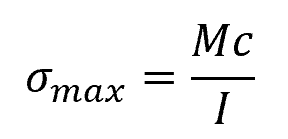
Where:
- σmax = maximum normal stress due to bending [Pa]
- c = distance from the neutral axis to the outermost fiber [m]
In practice, in order to find the maximum bending stress occurring in the beam, the location of the maximum bending moment is first determined using shear and bending moment diagrams. Once the location of the maximum moment is found, the above formula is used to calculate for the maximum bending stress at that particular location.
Example Problem
Problem: Consider a simply supported 20 cm x 30 cm beam with a length of 5 meters, subjected to a bending moment of 2500 N-m. Find the maximum bending stress experienced by the beam.
Solution:
First, we must calculate the moment of inertia of the beam. For a rectangular cross-section with width ‘b’ and height ‘h’, the moment of inertia (I) can be calculated as:
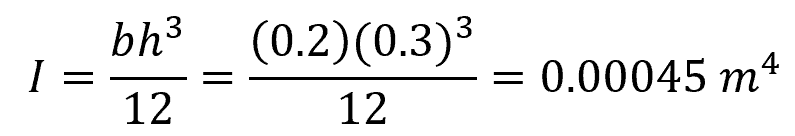
Next, find the distance (c) from the neutral axis to the farthest point of the cross-section. For a rectangular cross-section, this is half of the height:
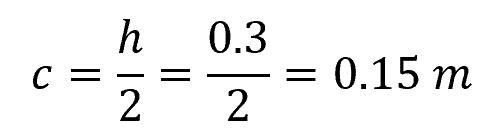
Finally, we can compute the maximum bending stress (σ) using the Bending Stress Formula:
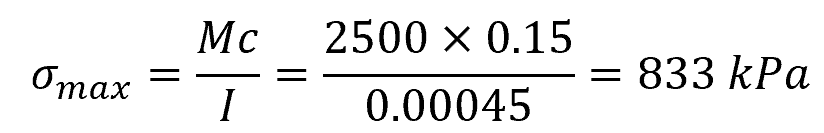
The maximum bending stress experienced by the beam at its outermost fiber is approximately 833 kPa.
