Section modulus is a geometric property of a cross section used in the design of beams or other flexural members that will experience deflection due to an applied bending moment. The units of section modulus are length^3.
There are two types of section moduli: elastic section modulus and plastic section modulus. Elastic section modulus applies to designs that are within the elastic limit of a material, which is the most common case. Often, “elastic section modulus” is referred to as simply “section modulus.
Section modulus is used in structural engineering to calculate the bending moment that will result in the yielding of a beam with the following equation:
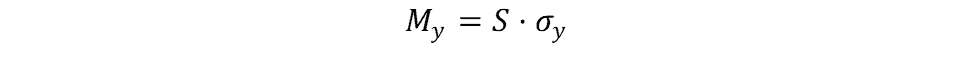
where
- S = section modulus
- σy = material’s yield strength
Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Beams in bending experience stresses in both tension and compression.
Section Modulus Calculators
Use the calculators below to calculate the elastic section moduli of common shapes such as rectangles, I-beams, circles, pipes, hollow rectangles, and c-channels that undergo bending. Consistent units are required for each calculator to get correct results.
Section Modulus of a Rectangle Calculator
The equation for calculating elastic section modulus of a rectangle is:
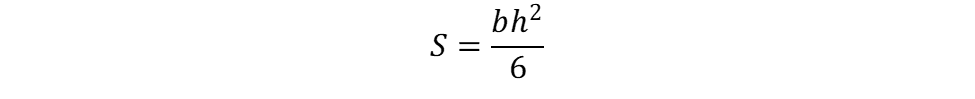
where
- b = section width
- h = section height

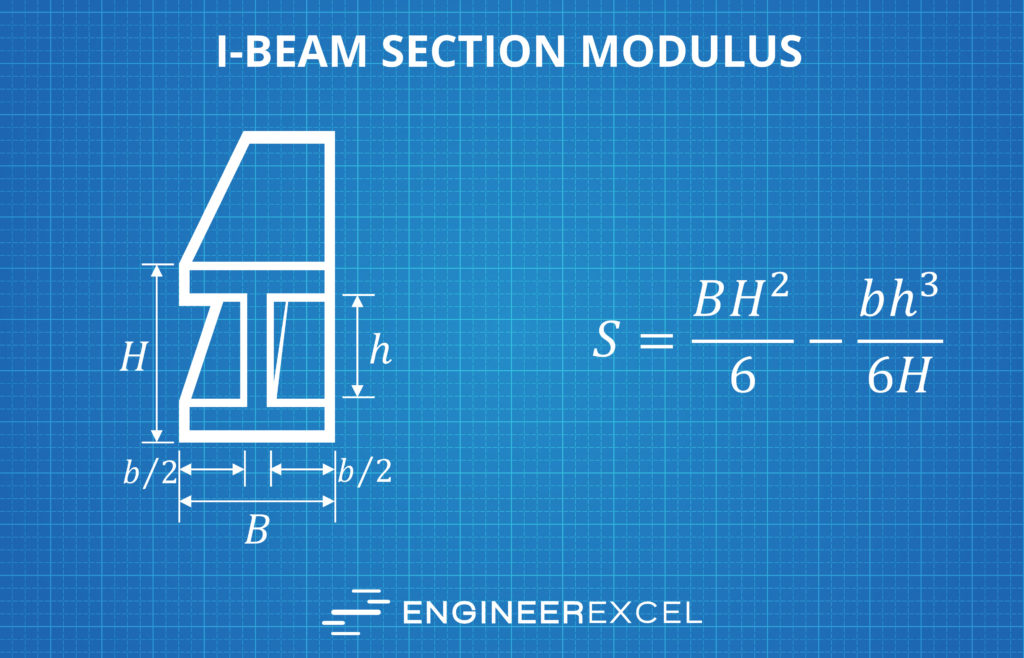
Section Modulus of an I-Beam Calculator
The elastic section modulus of an I-beam is calculated from the following equation:
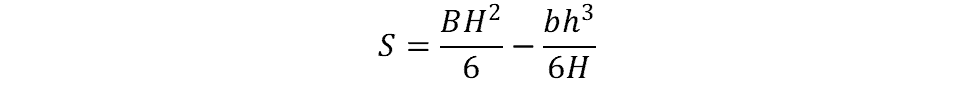
where
- B = flange width
- H = I-beam height
- b = flange width minus web width
- h = web height
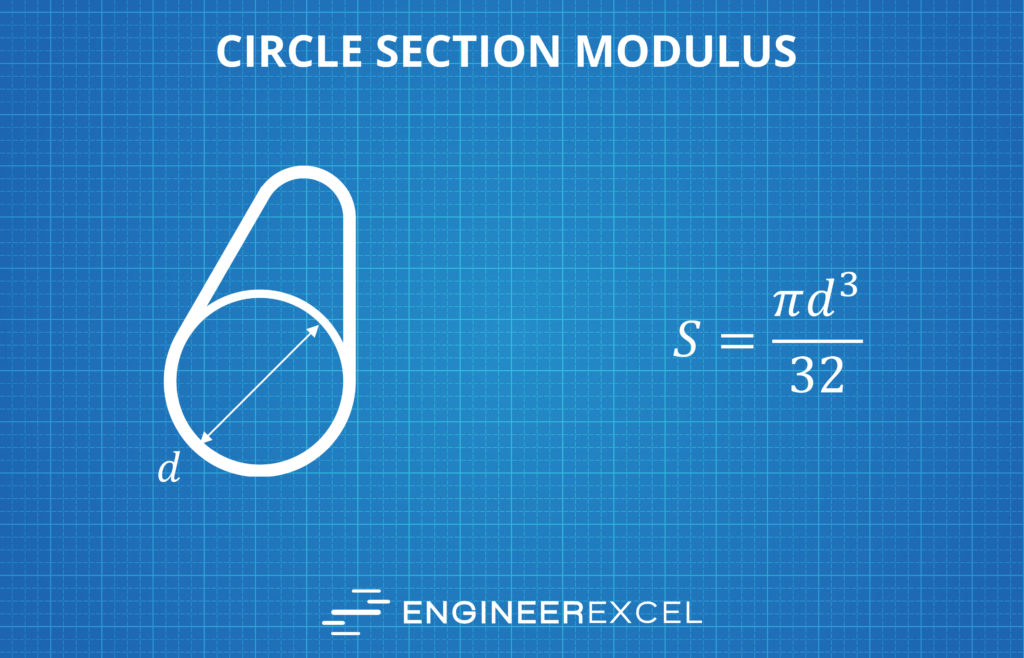
Section Modulus of a Circle Calculator
The equation below is used to calculate the elastic section modulus of a circle:
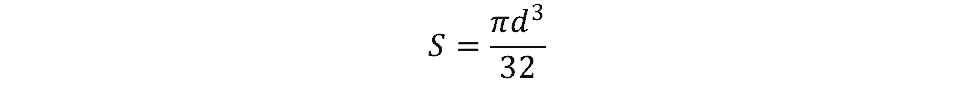
where
d = diameter of the circle
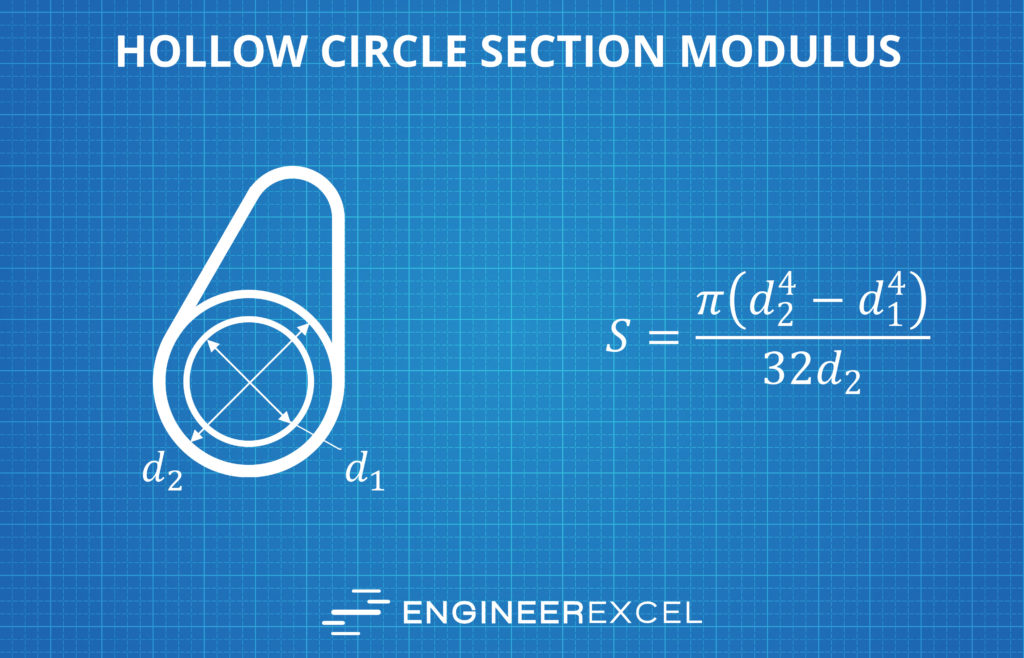
Section Modulus of a Hollow Circle Calculator
The formula for calculating elastic section modulus for a pipe is shown below:
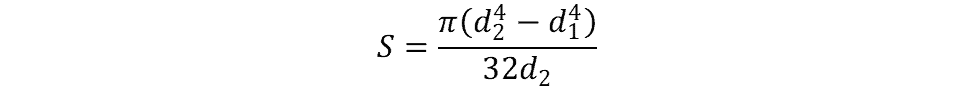
where
- d1 = inside diameter = 2 x inner radius
- d2 = outside diameter = 2 x outer radius
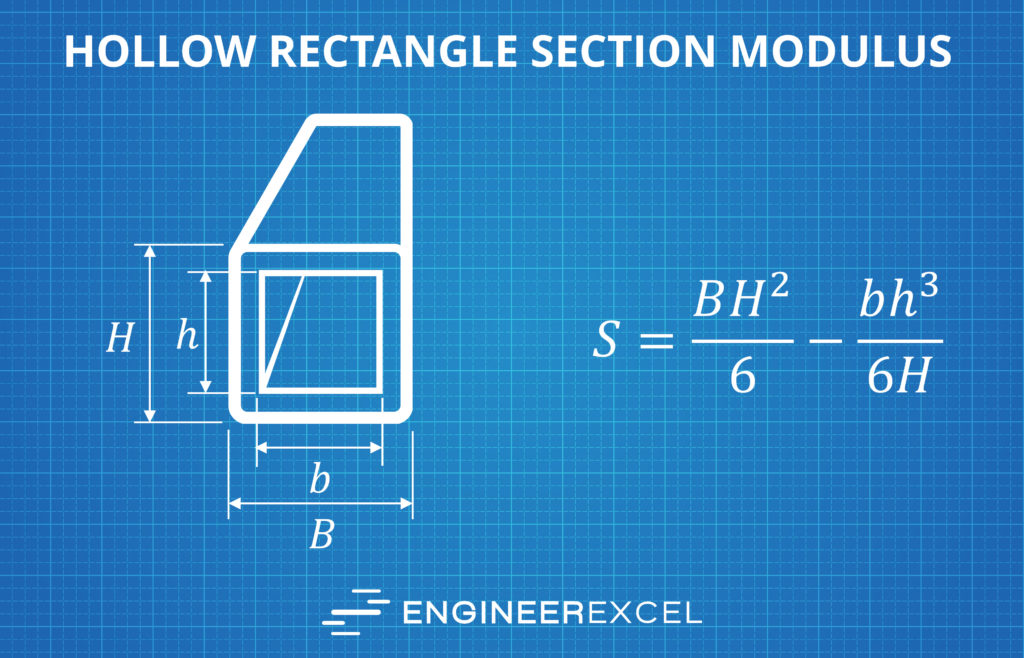
Section Modulus of a Hollow Rectangle Calculator
For a hollow rectangle, the elastic section modulus can be determined from the following formula:

where
- B = outside width
- H = outside height
- b = interior (hollow) width
- h = interior (hollow) height
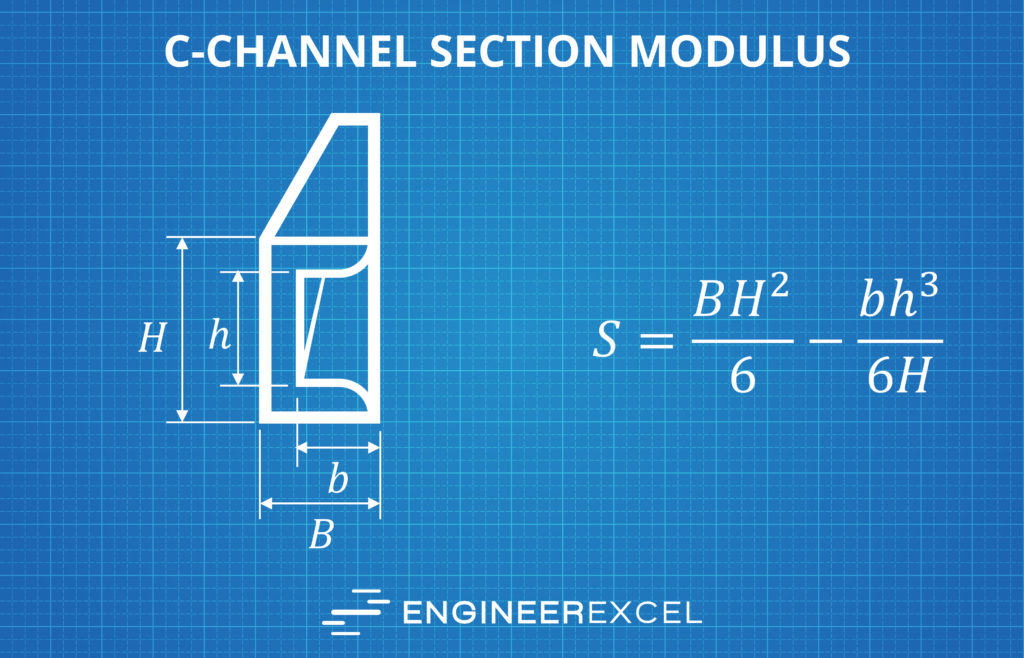
Section Modulus of a C-Channel Calculator
The elastic section modulus of C-channel is calculated from the following equation:
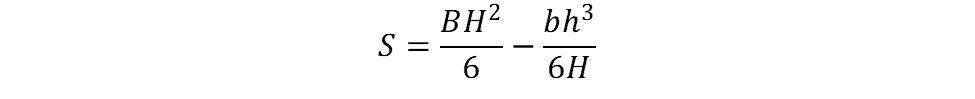
where
- B = flange width
- H = overall height
- b = flange width minus web thickness
- h = web height
What is the section modulus formula?
The general formula for elastic section modulus of a cross section is:
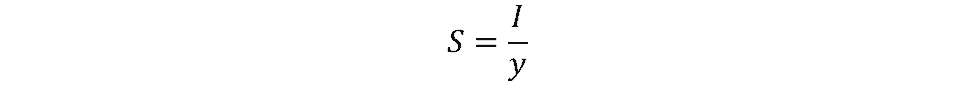
where
I = the area moment of inertia (or second moment of area)
y = the distance from the neutral axis to the outside edge of a beam
What is the required section modulus?
The required section modulus can be calculated if the bending moment and yield stress of the material are known. Consider the following example:
A beam made from A36 steel is to be subjected to a load of 120,000 lbf-in. Calculate the required section modulus with a factor of safety of 2.
Rearrange the equation from the beginning of this post into the following form:
The allowable stress in the

A36 steel is equal to the yield stress of 36,000 psi. Therefore, the required section modulus to achieve a safety factor of 2 in bending is calculated as shown below:

For this example problem, the required section modulus is 6.67 in3.
How do you find the section modulus of an irregular shape?
Even if a shape does not have a pre-defined section modulus equation, it’s still possible to calculate its section modulus.
Recall that the section modulus is equal to I/y, where I is the area moment of inertia. The definition of moment of inertia is
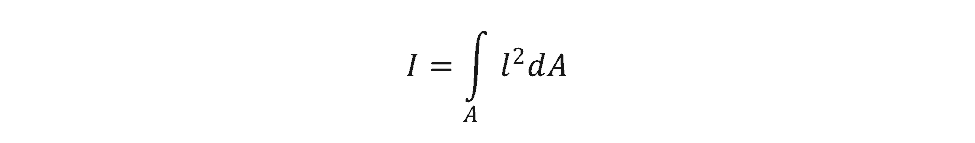
where
dA = the area of an element of the cross-sectional area of the irregular shape
l = the perpendicular distance from the element to the neutral axis passing through the centroid
Therefore, the section modulus of an irregular shape can be defined by
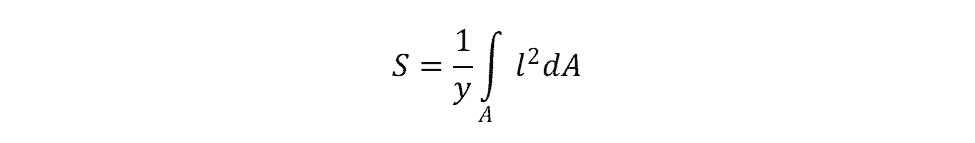
This can be a very difficult integration to perform with a high level of accuracy for an irregular shape. For that reason, it’s common to use specialized software to calculate the section modulus in these instances.
What is the difference between section modulus and plastic modulus?
When the term section modulus is used, it is typically referring to the elastic modulus. This is the most common usage, because it deals with materials that are within their elastic limit, or stresses less than the yield strength.
Plastic section modulus, however, is used when a material is allowed to yield and plastically deform. It is very rare that a section would be allowed to yield, and so plastic section modulus is rarely used.
What is the difference between moment of inertia and section modulus?
There are two cases in which the term “moment of inertia” is used:
- Area moment of inertia: a geometric cross-sectional property (also known as second moment of area)
- Mass moment of inertia or polar moment of inertia: resistance of a mass to changes in rotational velocity
Section modulus and area moment of inertia are closely related, however, as they are both properties of a beam’s cross-sectional area.
Area moment of inertia can be used to calculate the stress in a beam due to an applied bending moment at any distance from the neutral axis using the following equation:

where σ is the stress in the beam, y is the distance from the neutral axis passing through the centroid, and I is the area moment of inertia.
Since the stress is greatest at the farthest distance from the neutral axis, section modulus combines both the area moment of inertia and the maximum distance from the neutral axis into one term:
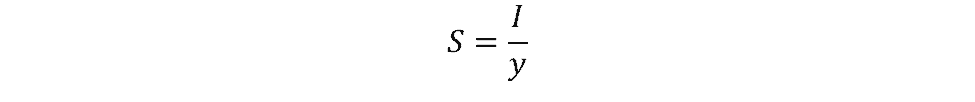
Therefore, the equation for maximum bending stress becomes:
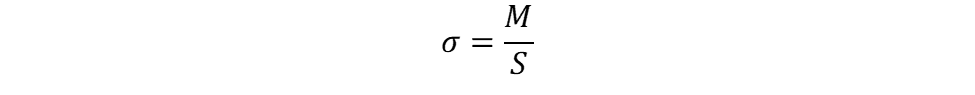
Section modulus and mass moment of inertia are entirely different properties altogether. Section modulus is a cross-section property with units of length^3. Mass moment of inertia is a mass property with units of mass*length^2.
How do you increase section modulus?
Section modulus can be increased along with the cross sectional area, although some methods are more efficient than others. Take for example, a rectangular cross section whose section modulus is defined by the following equation:

Doubling the width of the rectangle, b, will increase the section modulus by a factor of 2. However, doubling the height of the cross-section will increase the section modulus by a factor of 4. This would be a much more efficient way to use material to increase the section modulus.
