When a force is applied to a material, it undergoes deformation in two directions: the direction of the applied force and the direction perpendicular to the applied force. In the field of materials science and engineering, this material behavior is described by a property called the Poisson’s ratio.
Poisson’s Ratio Calculation
Poisson’s ratio is a fundamental property that describes the relationship between the lateral and the longitudinal strain of a material. Lateral strain refers to the deformation in the direction perpendicular to the applied force, while longitudinal strain refers to the deformation in the direction of the applied force.
In other words, it measures how much a material contracts or expands laterally when it is stretched or compressed longitudinally. For example, the material specimen below undergoes contraction along the y and z axes when stretched along the x axis.
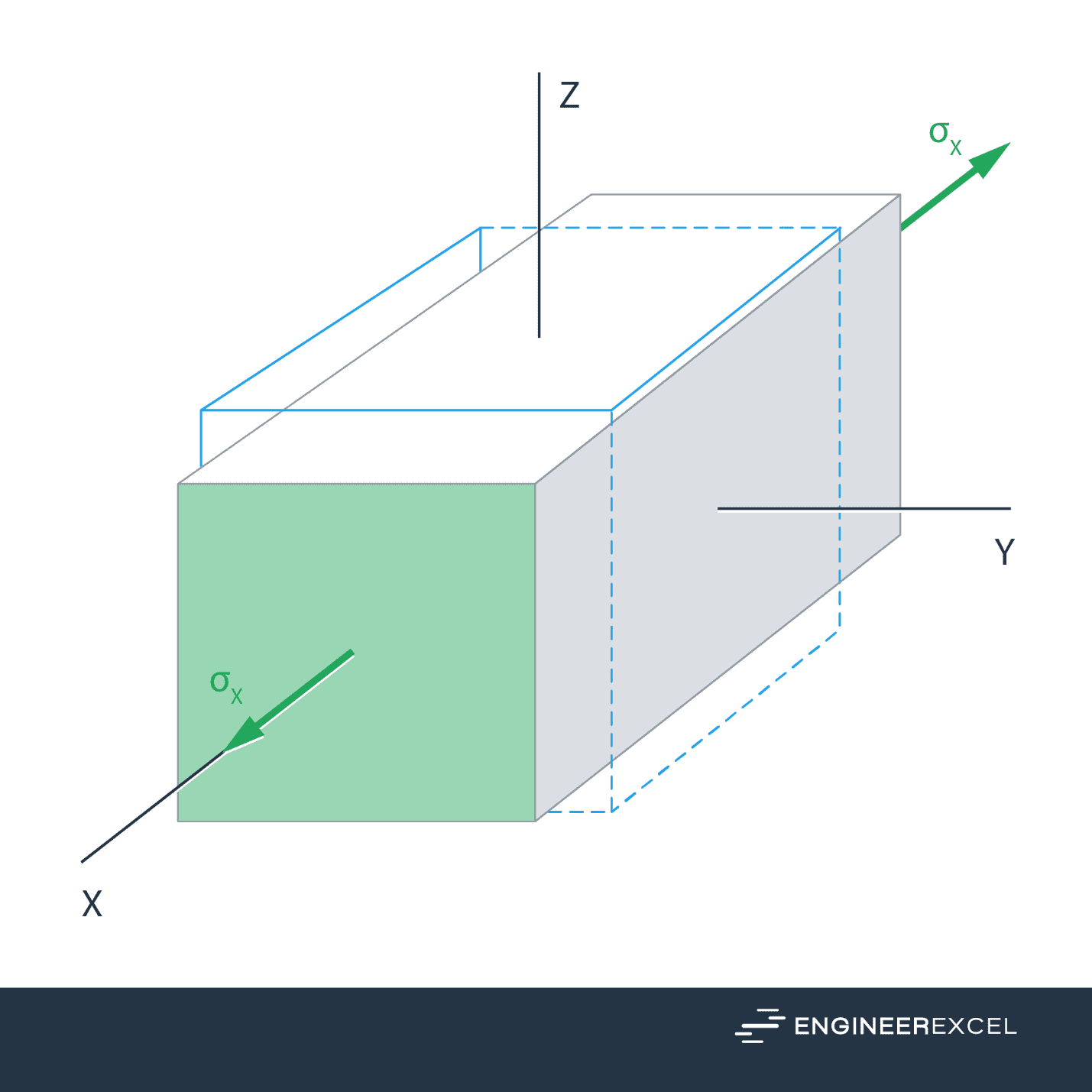
Calculating Poisson’s Ratio from Elongation

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
Following the definition above, Poisson’s ratio can be calculated from elongation using the formula:
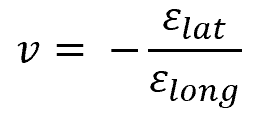
Where:
- v = Poisson’s ratio [unitless]
- εlat = lateral strain of the material [unitless]
- εlong = longitudinal strain of the material [unitless]
Remember that strain is the ratio between the change in length and the original length of the material, which can be mathematically expressed as:
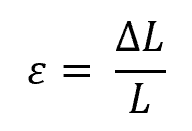
Where:
- ΔL = change in length of the material [m]
- L = original length of the material [m]
Notice that the formula for the Poisson’s ratio has a negative sign. This is so that most materials would have a positive Poisson’s ratio, considering that most materials contract when stretched and expand when compressed. Most materials resist change in volume more than they resist change in shape.
However, it is important to know that not all materials follow this behavior. Some materials, known as auxetic materials, expand laterally when stretched longitudinally and vice versa. Therefore, they have a negative Poisson’s ratio.
Auxetic materials are especially engineered for specific applications. Some examples include re-entrant foam which is normally used for shock absorption, auxetic honeycomb structures which are used to create lightweight but strong materials for aerospace applications, and auxetic textiles which are used to create new types of fabrics that are stretchier, more durable, and more breathable than traditional textiles.
Relating Poisson’s Ratio to Young’s Modulus, Bulk Modulus, and Shear Modulus
Young’s modulus, bulk modulus, and shear modulus are material properties that are used to describe the behavior of materials in the elastic region. The Young’s modulus is a measure of a material’s stiffness or resistance to axial deformation. It is defined as the ratio of axial stress to axial strain within the elastic limit of the material.
On the other hand, the bulk modulus is a measure of a material’s resistance to uniform compression or volume change when subjected to an external force. Mathematically, it is defined as the ratio of the change in pressure to the fractional change in volume when a material is subjected to a uniform pressure or stress.
Lastly, the shear modulus is a measure of a material’s resistance to transverse deformation when subjected to a shearing force. Mathematically, it is defined as the ratio of the shearing stress to the corresponding shear strain within the elastic limit of the material.
For homogeneous, elastic, and isotropic materials— that is, materials whose properties are independent of direction— the Poisson’s ratio can be related to the Young’s modulus, bulk modulus, and shear modulus using the following equations:
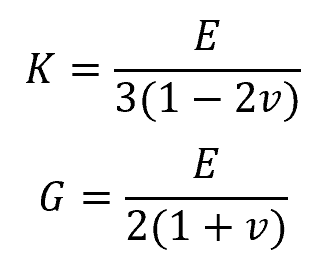
Where:
- K = bulk modulus [Pa]
- E = Young’s modulus [Pa]
- G = shear modulus [Pa]
Using Poisson’s Ratio to Find Strain
For a uniaxial loading along the x axis, the resulting strains can be calculated using the following equations:
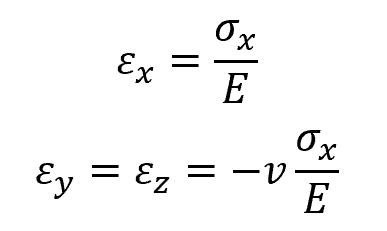
Where:
- εx, εy, εz = resulting strains along the x, y, and z axes, respectively [unitless]
- σx = axial stress along the x axis [Pa]
However, in reality, most structures can be simultaneously loaded in multiple directions. Hence, it is important to consider multiaxial stresses when finding the resulting strains. A free body diagram of a multiaxially loaded material is shown below:
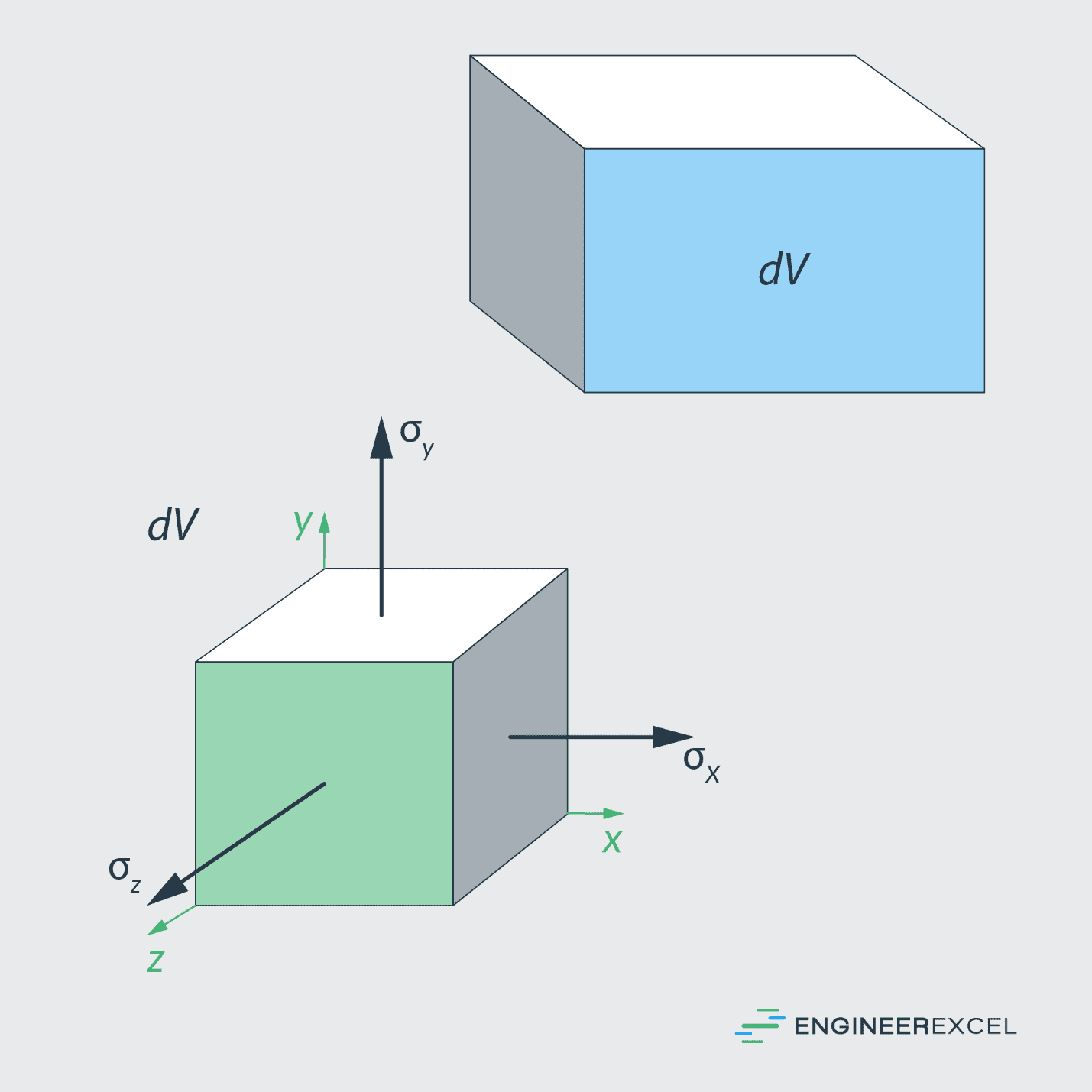
In this case, the strain equations become:
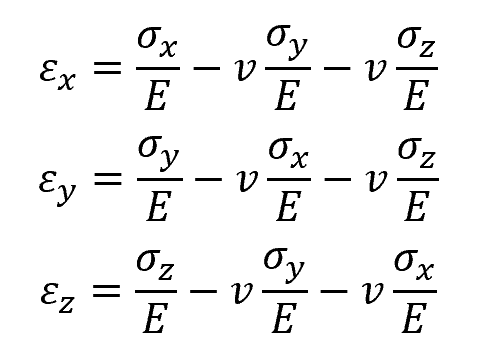
Where:
- σx, σy, σz = axial stresses along the x, y, and z axes [Pa]
Poisson’s Ratio of Different Materials
The value of the Poisson’s ratio depends on the type of material and its composition.
In isotropic and linearly elastic materials, Poisson’s ratio is in the range of -1 to 0.5. Auxetic materials lie in the negative range down to -1, while common typical materials lie in the positive range up to 0.5.
If the material is incompressible, then the Poisson’s ratio is equal to 0.5. Incompressible means that compressing the material in one direction will cause the same amount of expansion in the other directions, resulting in no volume change. An example of this is rubber.
Most engineering materials, for example steel or aluminum, have a Poisson’s ratio around 0.3. The Poisson’s ratio of some of the most common materials is listed in the table below:
In anisotropic solids— that is, solids that have different mechanical and physical properties in different directions— the value of the Poisson’s ratio depends on the direction of measurement. However, unlike in isotropic materials, this value is not bounded by the range between -1 to 0.5. Instead, the allowable range of Poisson’s ratio is expanded from negative infinity to positive infinity.
Also, it is important to note that the definition of Poisson’s ratio as a material constant is only valid for small strain values. If strain is sufficiently large, strain can affect the value of the Poisson’s ratio. In this case, the Poisson’s ratio should then be described as a function.
The value of Poisson’s ratio can even change over time. This is true for viscoelastic materials— materials that exhibit both viscous and elastic properties when subjected to deformation. These materials can dissipate energy over time, which means that they exhibit time-dependent mechanical behavior.
Particularly in transient tests such as creep and stress relaxation, when these materials undergo sinusoidal deformation, the Poisson’s ratio can vary depending on the frequency, and may even have a phase angle associated with it. For glassy polymers, the Poisson’s ratio is typically around 1/3. However, at higher temperatures or at lower frequencies, where the materials exhibits rubbery behavior, the stiffness decreases greatly and Poisson’s ratio approaches 1/2.
