An object’s polar moment of inertia is its ability to resist deflection due to an applied torque. It is largely based on the cross-section of an object along the axis to which torque is applied.
How Do You Calculate the Polar Moment of Inertia?
The twisting of an object will happen around the axis from where to calculate the polar moment of inertia. As an example, if you had a tube that was being twisted, the cross-sectional area needed for the calculation would be the area of the circular cross-section of the tube.
In essence, polar moment of inertia is an object’s (whether that be in the form of a beam, tube, or shaft) resistance to deformation (plastic or not) due to an applied torque. Note that torque is a twisting force, and torsion is the twist that arises from the applied torque. The polar moment of inertia is wholly dependent on the cross-sectional area of the twisting object, and not a result of material type.
The formula for polar moment of inertia is as follows. It is a double integral over the cross-sectional area:
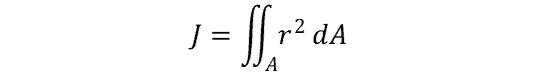

Elevate Your Engineering With Excel
Advance in Excel with engineering-focused training that equips you with the skills to streamline projects and accelerate your career.
where:
- J = polar moment of inertia (m4)
- r = distance to the element dA (m)
- dA = area differential element
This general formula is a little confusing, involving a double integral and what appears to be a radius term, despite not every cross-sectional area being a circle. Fortunately there are differing standard formulas to calculate the polar moment of inertia for cylinders of various cross sections. Let’s take a look at some of the most common:
Solid Circular Cross Section Polar Moment of Inertia
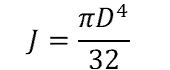
where:
- D = diameter of circle

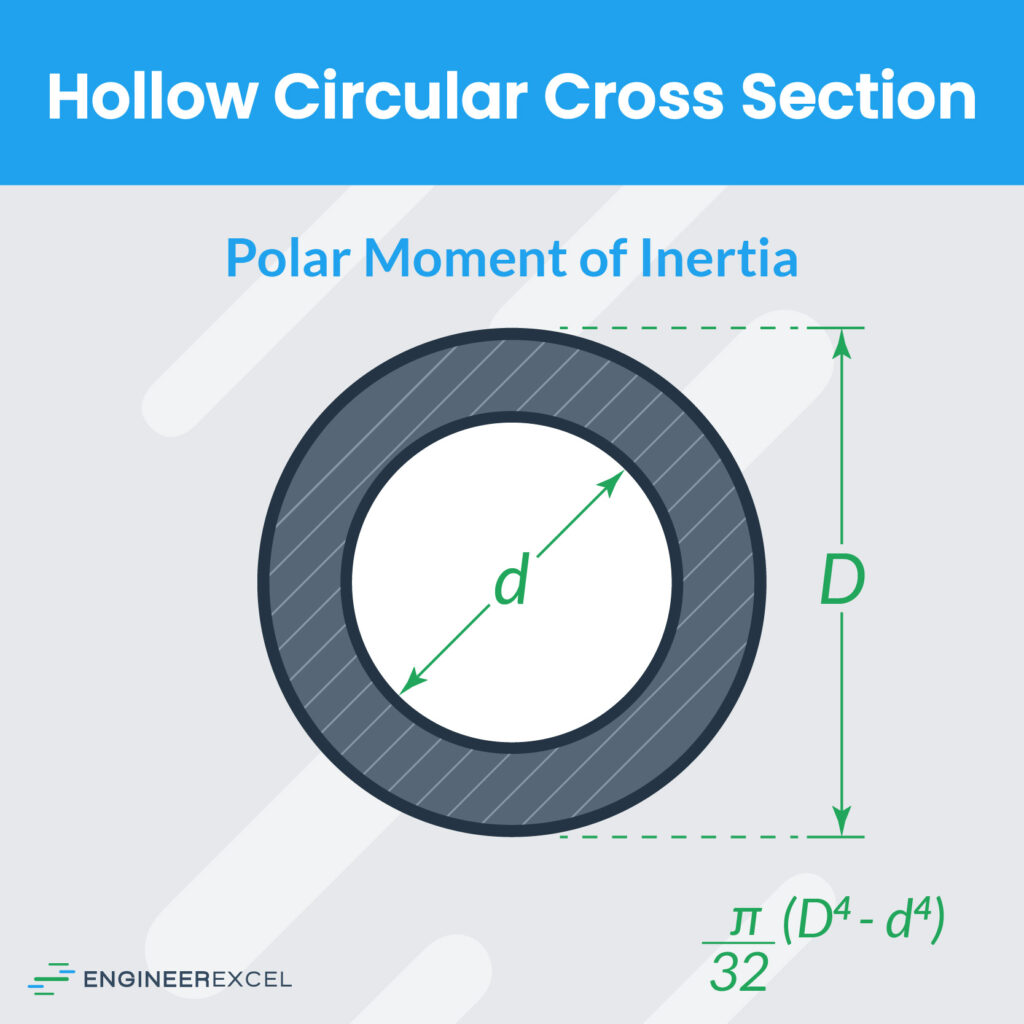
Hollow Circular Cross Section Polar Moment of Inertia

where:
- D = outer diameter of tube/circle (m)
- d = inner diameter of tube/circle (m)
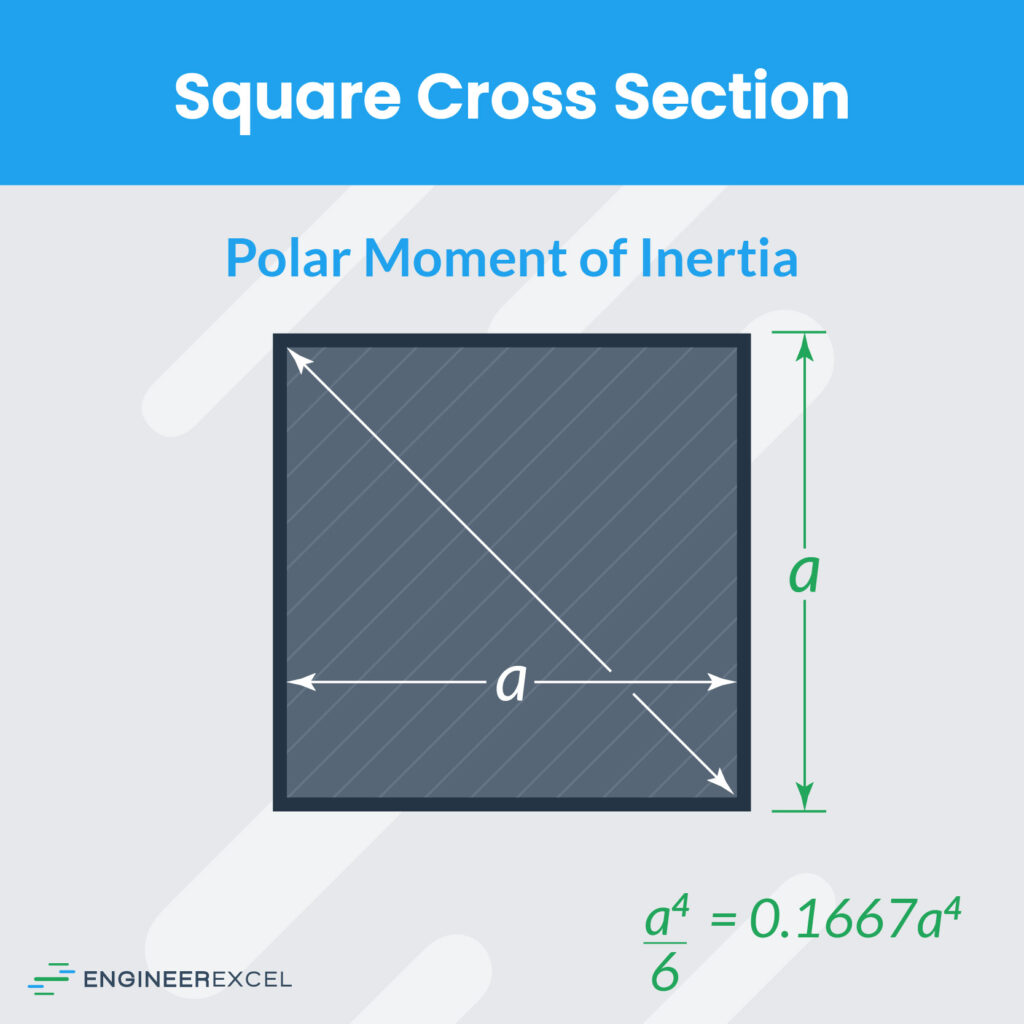
Square Cross Section Polar Moment of Inertia
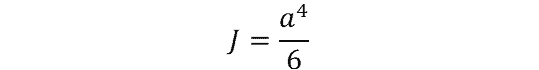
where:
- a = length of side (m)
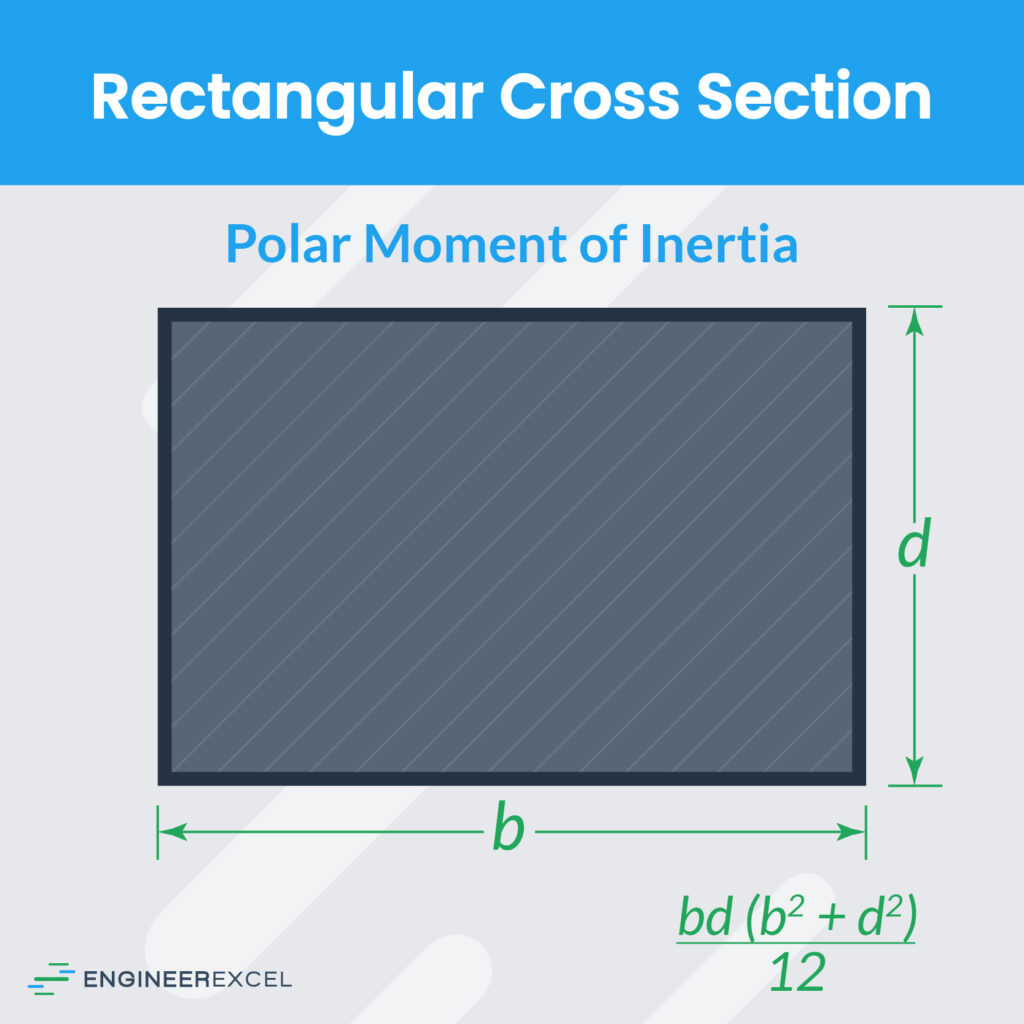
Rectangular Cross Section Polar Moment of Inertia
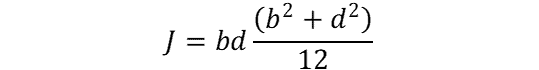
where:
- b/d = two lengths of sides (m)
These formulas have already done the double integration and are left in value plug-in simplifications. There are also simplified formulas for other common cross-sectional areas, like triangular, hexagonal, and variable shaped socket cylinders.
There are several things that influence the polar moment of inertia. And the greater the polar moment, the “stiffer” an object is, regardless of material makeup or shear modulus.
The formulas demonstrate that polar moment of inertia can be increased by increasing the size of the cylindrical object. This conclusion follows naturally from the fact that a larger object requires a larger force to meaningfully twist it!
For comparison, if you were to have a square cylinder versus a cylindrical cylinder with an equally size radius, then the square cylinder would have a higher polar moment of inertia. So why do we see more examples of circular cylinders in the real world? Well, there are several other factors to consider where square cross sections might perform worse, and circular cylinders mesh better for things like nuts, bearings, and washers.
The Difference Between Moment of Inertia and Polar Moment of Inertia
The moment of inertia, also known as the mass moment of inertia, is not the same thing as its polar counterpart. There are several other names this quality is also known as: angular mass, second moment of mass, and rotational inertia.
Rather than resistance to torque, the mass moment of inertia is an object’s ability to resist rotation or change in a rotational direction. It depends on a body’s mass distribution with respect to the axis of rotation, instead of its shape, although shape may factor into how that mass is in fact distributed. The formula for mass moment of inertia is:
For a point mass:
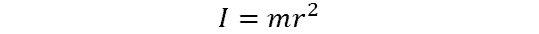
For a general body:
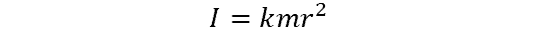
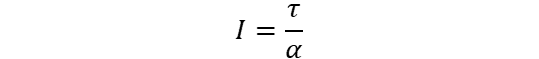
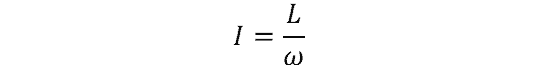
where:
- I = mass moment of inertia (kg-m2)
- m = mass (kg)
- r = distance between axis and rotational mass (m)
- k = inertial constant, dependent on shape of body (unitless)
- τ = applied torque (N-m)
- α = angular acceleration (rad/sec2)
- L = angular momentum (kg-m2/s)
- ω = angular velocity (rad/s)
Here it is evident that mass moment of inertia has much more to do with a body’s weight and rotational energy, and distance away from the rotational axis than its shape, although shape can play a factor. The polar moment of inertia can be thought of as a distribution of area relative to the rotational axis, whereas mass moment is concerned with the mass distribution around the same.
What is Polar Moment of Inertia vs Product of Inertia?
The product of inertia is another way to study how mass is distributed within a rotating object, and whether or not that object is rotating around an axis that makes rotation symmetrical. If an object is symmetrical around its rotational axis, then the product of inertia is zero. If an object is not distributed evenly around its rotational axis, then it will have some product of inertia.
The product of inertia is more related to the mass moment of inertia rather than the polar moment. It may be positive, negative, or zero depending on where the object lies in relation to the coordinate axes. If there is in fact a non-zero product of inertia, one can produce a theoretical situation in which the rotation is symmetrical, and the product is zero by shifting the axes to a point where they are known as the “principal axes”.
If this all sounds confusing, it may be best to consider an example. A car tire that is working properly will rotate evenly and symmetrically, helping to roll the car in a smooth manner. A tire that suddenly is not rotating perfectly symmetrical axis, and instead is either misshapen or rotating on an axis that is not at the center of the wheel, will make the car drive in a bumpy manner. In essence, if an object is said to have a product of inertia, then it will rotate in a way that makes it “wobble”.
